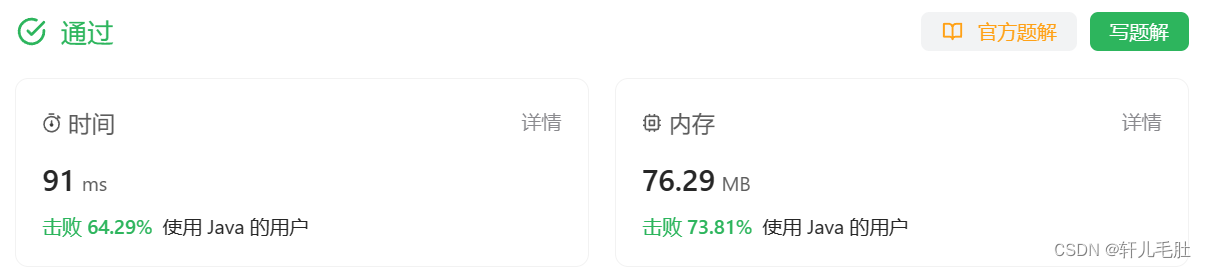
题目：

2003. 每棵子树内缺失的最小基因值

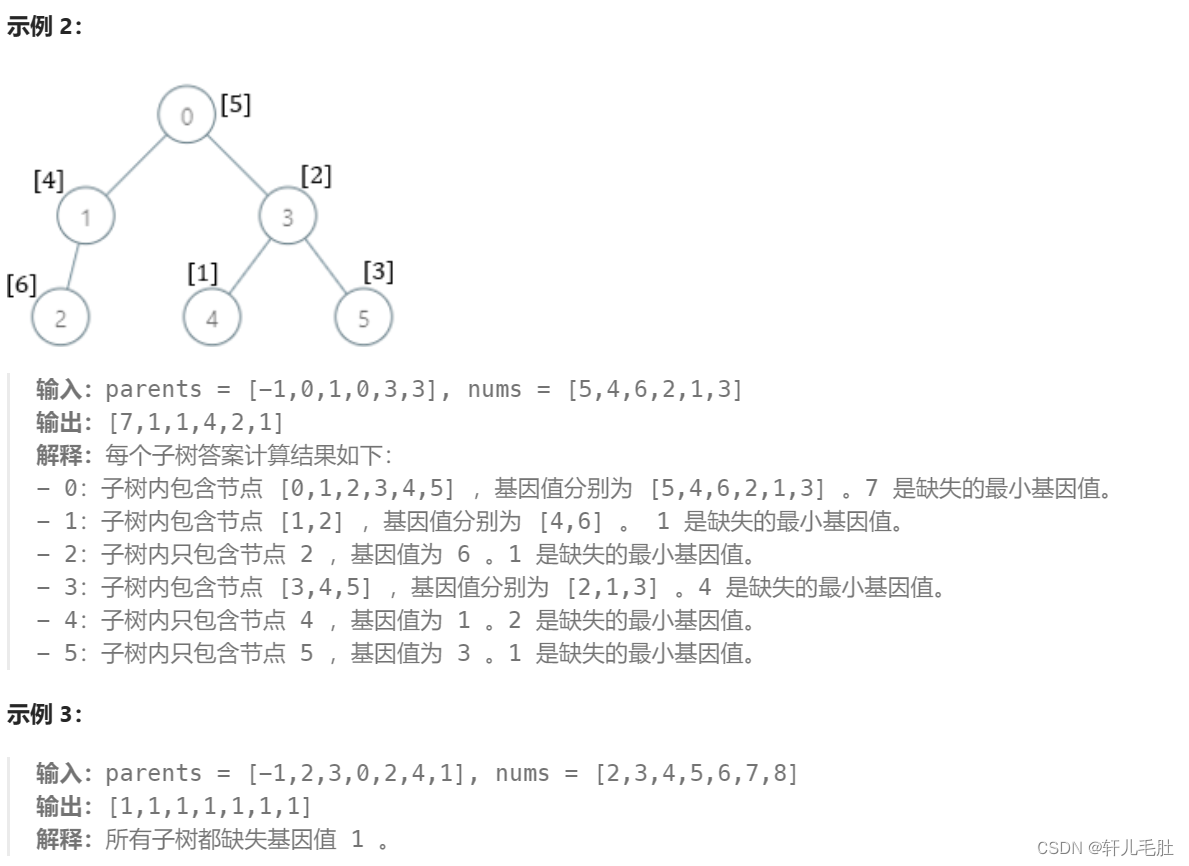
有一棵根节点为 0 的 家族树 ，总共包含 n 个节点，节点编号为 0 到 n - 1 。给你一个下标从 0 开始的整数数组 parents ，其中 parents[i] 是节点 i 的父节点。由于节点 0 是 根 ，所以 parents[0] == -1 。

总共有 105 个基因值，每个基因值都用 闭区间 [1, 105] 中的一个整数表示。给你一个下标从 0 开始的整数数组 nums ，其中 nums[i] 是节点 i 的基因值，且基因值 互不相同 。

请你返回一个数组 ans ，长度为 n ，其中 ans[i] 是以节点 i 为根的子树内 缺失 的 最小 基因值。

节点 x 为根的 子树 包含节点 x 和它所有的 后代 节点。

提示：

• n == parents.length == nums.length
• 2 <= n <= 105
• 对于 i != 0 ，满足 0 <= parents[i] <= n - 1
• parents[0] == -1
• parents 表示一棵合法的树。
• 1 <= nums[i] <= 105
• nums[i] 互不相同。

解答：

代码：

写法1：DFS

class Solution {
    public int[] smallestMissingValueSubtree(int[] parents, int[] nums) {
        int n=parents.length;
        int[] ans=new int[n];
        Arrays.fill(ans,1);
        int node=-1;
        for(int i=0;i<n;i++){
            if(nums[i]==1){
                node=i;//出发点
                break;
            }
        }
        if(node<0){//不存在基因值为1的点
            return ans;
        }

        //建树
        List<Integer>[] g=new ArrayList[n];
        Arrays.setAll(g,e->new ArrayList<>());
        for(int i=1;i<n;i++){
            g[parents[i]].add(i);
        }

        Set<Integer> vis=new HashSet<>();
        int mex=2;//缺失的最小基因值
        while(node>=0){
            dfs(node,g,vis,nums);
            while(vis.contains(mex)){//node子树中包含这个基因值
                mex++;
            }
            ans[node] =mex;//缺失的最小基因值
            node=parents[node];//往上走
        }
        return ans;
    }
    //遍历子树
    private void dfs(int x,List<Integer>[] g,Set<Integer> vis,int[] nums){
        vis.add(nums[x]);//标记基因值
        for(int son:g[x]){
            if(!vis.contains(nums[son])){
                dfs(son,g,vis,nums);
            }
        }
    }
}

写法2：非递归

改为手动记录接下来要访问的点。

此外，假设 pre是下面的点（从 pre往上走到当前节点），那么遍历子树的时候可以跳过 pre子树。

 

class Solution {
    public int[] smallestMissingValueSubtree(int[] parents, int[] nums) {
        int n = parents.length;
        int[] ans = new int[n];
        Arrays.fill(ans, 1);
        int node = -1;
        for (int i = 0; i < n; i++) {
            if (nums[i] == 1) {
                node = i; // 出发点
                break;
            }
        }
        if (node < 0) { // 不存在基因值为 1 的点
            return ans;
        }

        // 建树
        List<Integer>[] g = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList<>());
        for (int i = 1; i < n; i++) {
            g[parents[i]].add(i);
        }

        Set<Integer> vis = new HashSet<>();
        List<Integer> nodes = new ArrayList<>(); // 保存接下来需要遍历的点
        int mex = 2; // 缺失的最小基因值
        int pre = -1;
        while (node >= 0) {
            vis.add(nums[node]); // 标记基因值
            for (int son : g[node]) {
                if (son != pre) { // pre 子树已经遍历过了
                    nodes.add(son); // 保存接下来需要遍历的点
                }
            }
            while (!nodes.isEmpty()) {
                int x = nodes.remove(nodes.size() - 1);
                vis.add(nums[x]); // 标记基因值
                nodes.addAll(g[x]); // 保存接下来需要遍历的点
            }
            while (vis.contains(mex)) { // node 子树包含这个基因值
                mex++;
            }
            ans[node] = mex; // 缺失的最小基因值
            pre = node; // 下一轮循环不会遍历 pre 子树
            node = parents[node]; // 往上走
        }
        return ans;
    }
}

写法3： 非递归+数组

class Solution {
    public int[] smallestMissingValueSubtree(int[] parents, int[] nums) {
        int n = parents.length;
        int[] ans = new int[n];
        Arrays.fill(ans, 1);
        int node = -1;
        for (int i = 0; i < n; i++) {
            if (nums[i] == 1) {
                node = i; // 出发点
                break;
            }
        }
        if (node < 0) { // 不存在基因值为 1 的点
            return ans;
        }

        // 建树
        List<Integer>[] g = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList<>());
        for (int i = 1; i < n; i++) {
            g[parents[i]].add(i);
        }

        boolean[] vis = new boolean[n + 2];
        List<Integer> nodes = new ArrayList<>(); // 保存接下来需要遍历的点
        int mex = 2; // 缺失的最小基因值
        int pre = -1;
        while (node >= 0) {
            vis[Math.min(nums[node], n + 1)] = true; // 标记基因值
            for (int son : g[node]) {
                if (son != pre) { // pre 子树已经遍历过了
                    nodes.add(son); // 保存接下来需要遍历的点
                }
            }
            while (!nodes.isEmpty()) {
                int x = nodes.remove(nodes.size() - 1);
                vis[Math.min(nums[x], n + 1)] = true; // 标记基因值
                nodes.addAll(g[x]); // 保存接下来需要遍历的点
            }
            while (vis[mex]) { // node 子树包含这个基因值
                mex++;
            }
            ans[node] = mex; // 缺失的最小基因值
            pre = node; // 下一轮循环不会遍历 pre 子树
            node = parents[node]; // 往上走
        }
        return ans;
    }
}

结果：