AB试验（七）利用Python模拟A/B试验

到现在，我相信大家理论已经掌握了，轮子也造好了。但有的人是不是总感觉还差点什么？没错，还缺了实战经验。对于AB实验平台完善的公司 ，这个经验不难获得，但有的同学或多或少总有些原因无法接触到AB实验。所以本文就告诉大家，如何利用Python完整地进行一次A/B试验模拟。

现在，前面造好的轮子ABTestFunc.py就起到关键作用了

from faker import Faker
from faker.providers import BaseProvider, internet 
from random import randint
from scipy.stats import bernoulli
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split 
from scipy import stats
from collections import defaultdict
import toad 
import matplotlib.pyplot as plt
import seaborn as sns
import math

# 绘图初始化
%matplotlib inline
sns.set(style="ticks")
plt.rcParams['axes.unicode_minus']=False # 用来正常显示负号
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号

# 导入自定义模块
import sys
sys.path.append("/Users/heinrich/Desktop/Heinrich-blog/数据分析使用手册")
from ABTestFunc import *

上述自定义模块ABTestFunc如果有需要的同学可关注公众号HsuHeinrich，回复【AB试验-自定义函数】自动获取～

均值类指标实验模拟

实验前准备

• 背景：某app想通过优化购物车来提高用户的人均消费，遂通过AB实验检验优化效果。

• 实验前设定
  • 实验为双尾检验
  • 实验分流为50%/50%
  • 显著性水平为5%
  • 检验功效为80%

# 实验设定
alpha=0.05
power=0.8
beta=1-power

确定目标和假设

• 目标：提高人均消费
• 假设：选择商品时，醒目提示各商品优惠金额，并按照优惠截止日期排序，提高紧促感。

确定指标

• 评价指标：人均购买金额
• 护栏指标：样本比例、特征分布一致

确定实验单位

• 用户ID

样本量估算

• 模拟历史样本

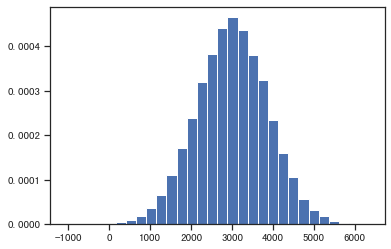
# 假设用户的购买金额服从正态分布
# 模拟过去一段时间的用户购买金额
np.random.seed(0)
pays=np.random.normal(2999, 876, 50000)
plt.hist(pays, 30, density=True)
plt.show()

# 输出当前消费金额的均值
print(pays.mean())
# 输出当前消费金额的方差
print(np.std(pays, ddof=1))
# 计算历史数据的波动区间，并假设此次提升高于最大波动上限
print(numbers_cal_ci(pays))

2995.676447900933
873.0773017854648
[2988.0237285541257, 3003.3291672477403]

• 依据提升情况计算样本量

# 当前消费均值为2996，方差为873，波动上限为3003。
# 假设此次实验能提高消费金额至3050元
u1=2996
u2=3050
s=np.std(pays, ddof=1)

n1=n2=numbers_cal_sample_third(u1, u2, s)
print(2*n1)

8210

随机分组

• CR法

测试时间的估算

# 假设每天用户流量680，且用户在周终于周末的购买行为不一致，因此至少包含一周的时间
test_time=max(math.ceil(2*n1/680), 7)
print(test_time)

13

实施测试

• 测试过程无明显异常
• 模拟实验数据产生，并在结束时收集数据

# 自定义数据
fake = Faker('zh_CN')
class MyProvider(BaseProvider):
    def myCityLevel(self):
        cl = ["一线", "二线", "三线", "四线+"]
        return cl[randint(0, len(cl) - 1)]
    def myGender(self):
        g = ['F', 'M']
        return g[randint(0, len(g) - 1)]
    def myDevice(self):
        d = ['Ios', 'Android']
        return d[randint(0, len(d) - 1)]
fake.add_provider(MyProvider)

# 构造假数据，模拟实验过程产生的样本数据的特征
uid=[]
cityLevel=[]
gender=[]
device=[]
age=[]
activeDays=[]
for i in range(8225):
    uid.append(i+1)
    cityLevel.append(fake.myCityLevel())
    gender.append(fake.myGender())
    device.append(fake.myDevice())
    age.append(fake.random_int(min=18, max=45)) # 年龄分布
    activeDays.append(fake.random_int(min=0, max=7)) # 近7日活跃分布
    
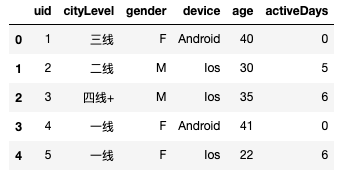
raw_data= pd.DataFrame({'uid':uid,
                        'cityLevel':cityLevel,
                        'gender':gender,
                        'device':device,
                        'age':age,
                        'activeDays':activeDays,
                       })

raw_data.head()

# 数据随机切分，模拟实验分流
test, control= train_test_split(raw_data.copy(), test_size=.5, random_state=0)
# 模拟用户购买金额
np.random.seed(1)
test['pays']=np.random.normal(3049, 850, test.shape[0])
control['pays']=np.random.normal(2999, 853, control.shape[0])
# 数据拼接,模拟数据收集结果
test['flag'] = 'test'
control['flag'] = 'control'
df = pd.concat([test, control])

分析测试结果

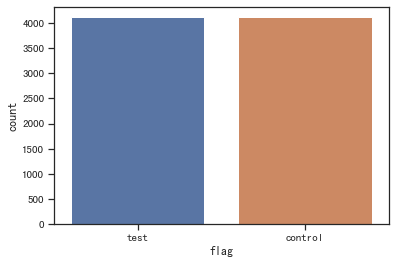
• 样本比例合理性检验

# 查看样本比例
sns.countplot(x='flag', data=df)
plt.show()

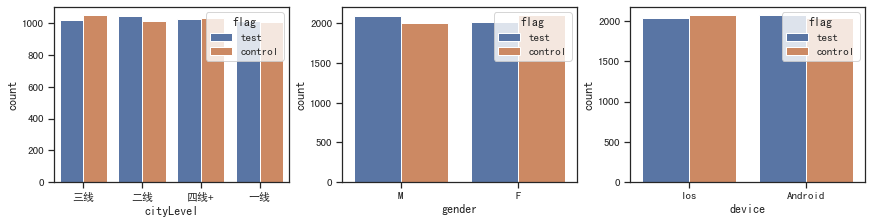
# 查看离散变量的分布
fig, ax =plt.subplots(1, 3, constrained_layout=True, figsize=(12, 3))
for i, x in enumerate(['cityLevel', 'gender', 'device']):
    sns.countplot(x=x, data=df, hue='flag', ax=ax[i])
plt.show()

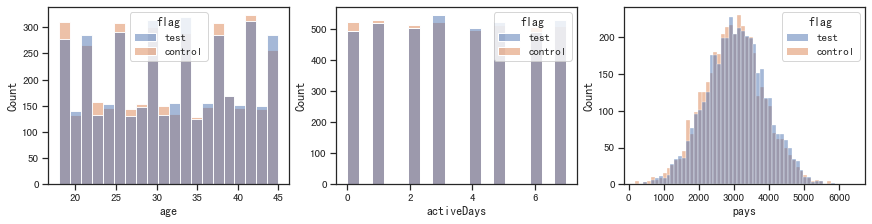
# 查看连续变量的分布
fig, ax =plt.subplots(1, 3, constrained_layout=True, figsize=(12, 3))
for i, x in enumerate(['age', 'activeDays', 'pays']):
    sns.histplot(x=x, data=df, hue='flag', ax=ax[i])
plt.show()

# 检验样本比例一致性
n1=control.size
n2=test.size
p1=p2=0.5
two_sample_proportion_test(n1, n2, p1, p2)

两样本比例校验: 通过

• 样本特征一致性校验

# 检验特征分布一致性
cols=['cityLevel', 'gender', 'device', 'age', 'activeDays']
feature_dist_ks(cols, test, control)

cityLevel: 相似
gender: 相似
device: 相似
age: 相似
activeDays: 相似

• 显著性校验

# 显著性检验
numbers_cal_significant(test['pays'], control['pays'])

方差齐性校验结果：方差相同

(3.1882855769529668,
 0.0014365540563265368,
 [23.101471736420166, 96.85309892416026])

p值小于5%，置信区间不包含0且最小提升为23，明显高于自然波动的上线。因此可以认为此次购物车优化实验有助于提高用户的人均消费

• 拓展-维度下钻分析

# 进行维度下钻分析，采用BH法进行多重检验校正
feature=[]
value=[]
pvaules=[]
for x in ['cityLevel', 'gender', 'device']:
    for i in df[x].unique():
        feature.append(x)
        value.append(i)
        # 构造细分维度的样本
        te=test[test[x]==i]
        co=control[control[x]==i]
        # 计算细分维度的p值
        p=numbers_cal_significant(te['pays'], co['pays'], levene_print=False)[1]
        pvaules.append(p)
    
df_multiple=pd.DataFrame({'feature':feature,
                        'value':value,
                        'pvaules':pvaules
                       })
df_multiple

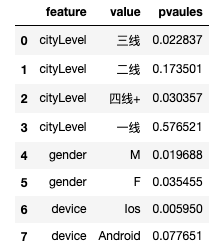
# 多重检验校正
print(multiple_tests_adjust(df_multiple['pvaules']))
df_multiple['pvaules_correct']=multiple_tests_adjust(df_multiple['pvaules'])[1]
df_multiple['reject']=multiple_tests_adjust(df_multiple['pvaules'])[0]
df_multiple

(array([False, False, False, False, False, False,  True, False]), array([0.05672733, 0.19828707, 0.05672733, 0.57652105, 0.05672733,
       0.05672733, 0.04760055, 0.10353442]), 0.00625)

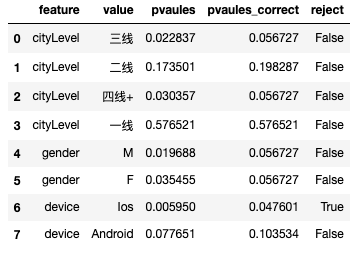
维度下钻发现，只有iOS设备的用户存在显著提升

实验报告

# 关键数据展示

# 样本及均值
print('control:' ,f'sample {control.shape[0]} / mean:{control.pays.mean()}')
print('test:' ,f'sample {test.shape[0]} / mean:{test.pays.mean()}')
# 实验周期
print('times:', test_time)
# diff
print('diff:', test['pays'].mean()-control['pays'].mean())
# p值
print('p-value:', numbers_cal_significant(test['pays'], control['pays'], levene_print=False)[1])
# diff-置信区间
print('diff-ci:', numbers_cal_significant(test['pays'], control['pays'], levene_print=False)[2])
# 维度下钻结果
print('dim-result:')
for i,v in zip(df_multiple.value,df_multiple.reject):
    print(' '*2,f'{i}:{v}')

control: sample 4113 / mean:3000.5565990602113
test: sample 4112 / mean:3060.533884390513
times: 13
diff: 59.977285330301584
p-value: 0.0014365540563265368
diff-ci: [23.101471736420166, 96.85309892416026]
dim-result:
   三线:False
   二线:False
   四线+:False
   一线:False
   M:False
   F:False
   Ios:True
   Android:False

• 实验13天，收集到实验组数据4112，对照组4113，共计8225。
• 实验过程无异常，实验组人均购买金额为3061元，较对照组提高60元
• 整体上，实验组的提升是显著的，且提升范围在[23, 97]元之间
• 通过维度下钻，发现实验组仅在Ios设备用户有显著提升

概率类指标实验模拟

实验前准备

• 背景：某音乐app想通过优化功能提示提高用户功能使用率。

• 实验前设定
  • 实验为双尾检验
  • 实验分流为50%/50%
  • 显著性水平为5%
  • 检验功效为80%

# 实验设定
alpha=0.05
power=0.8
beta=1-power

确定目标和假设

• 目标：提高【把喜欢的音乐加入收藏夹】功能的使用率
• 假设：用户从未使用过这个功能，且播放同一首歌到达4次时，在播放第5次进行弹窗提醒可以把喜欢的音乐加入收藏夹

确定指标

• 评价指标：【把喜欢的音乐加入收藏夹】功能的使用率
• 护栏指标：样本比例、特征分布一致

确定实验单位

• 用户ID

样本量估算

• 模拟历史样本

# 假设用户的购买金额服从正态分布
# 模拟过去一段时间的用户【把喜欢的音乐加入收藏夹】
np.random.seed(1)
collect=stats.bernoulli.rvs(0.02, size=20000, random_state=0)
plt.hist(collect, 30, density=True)
plt.show()

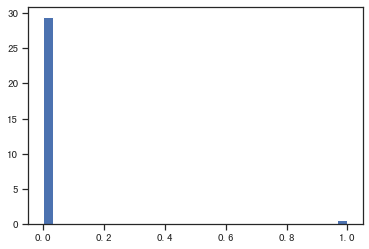
# 输出当前【把喜欢的音乐加入收藏夹】功能的使用率
print(collect.mean())
# 计算历史数据的波动区间，并假设此次提升高于最大波动上限
print(prob_cal_ci(0.02, 20000))

0.0197
[0.01805973464591045, 0.02194026535408955]

• 依据提升情况计算样本量

# 当前转化率为0.02，波动上限为0.0219。
# 假设此次实验能提高使用率至0.022
p1=0.02
p2=0.022

n1=n2=prob_cal_sample_third(p1, p2)
print(2*n1)

161276

随机分组

• CR法

测试时间的估算

# 假设每天符合条件用户流量1.7w，且用户在周终于周末的听音乐行为不一致，因此至少包含一周的时间
test_time=max(math.ceil(2*n1/17000), 7)
print(test_time)

10

实施测试

• 测试过程无明显异常
• 模拟实验数据产生，并在结束时收集数据

# 自定义数据
fake = Faker('zh_CN')
class MyProvider(BaseProvider):
    def myCityLevel(self):
        cl = ["一线", "二线", "三线", "四线+"]
        return cl[randint(0, len(cl) - 1)]
    def myGender(self):
        g = ['F', 'M']
        return g[randint(0, len(g) - 1)]
    def myDevice(self):
        d = ['Ios', 'Android']
        return d[randint(0, len(d) - 1)]
fake.add_provider(MyProvider)

# 构造假数据，模拟实验过程产生的样本数据的特征
uid=[]
cityLevel=[]
gender=[]
device=[]
age=[]
activeDays=[]
for i in range(161280):
    uid.append(i+1)
    cityLevel.append(fake.myCityLevel())
    gender.append(fake.myGender())
    device.append(fake.myDevice())
    age.append(fake.random_int(min=18, max=45)) # 年龄分布
    activeDays.append(fake.random_int(min=0, max=7)) # 近7日活跃分布
    
raw_data= pd.DataFrame({'uid':uid,
                        'cityLevel':cityLevel,
                        'gender':gender,
                        'device':device,
                        'age':age,
                        'activeDays':activeDays,
                       })

raw_data.head()

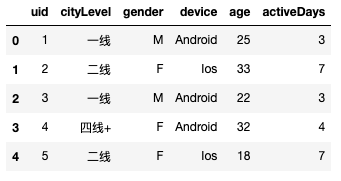
# 数据随机切分，模拟实验分流
test, control= train_test_split(raw_data.copy(), test_size=.5, random_state=0)
# 模拟用户收藏转化率
test['collect']=stats.bernoulli.rvs(0.023, size=test.shape[0], random_state=0)
control['collect']=stats.bernoulli.rvs(0.02, size=control.shape[0], random_state=0)
# 数据拼接,模拟数据收集结果
test['flag'] = 'test'
control['flag'] = 'control'
df = pd.concat([test, control])

分析测试结果

• 样本比例合理性检验

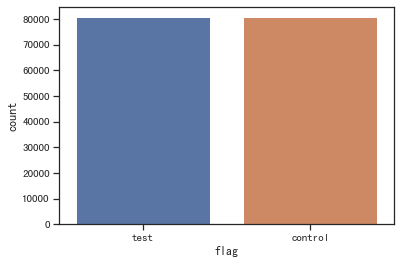
# 查看样本比例
sns.countplot(x='flag', data=df)
plt.show()

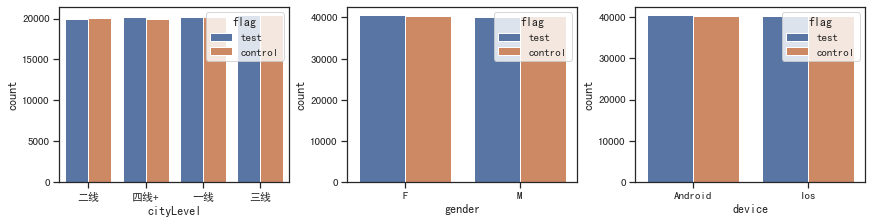
# 查看离散变量的分布
fig, ax =plt.subplots(1, 3, constrained_layout=True, figsize=(12, 3))
for i, x in enumerate(['cityLevel', 'gender', 'device']):
    sns.countplot(x=x, data=df, hue='flag', ax=ax[i])
plt.show()

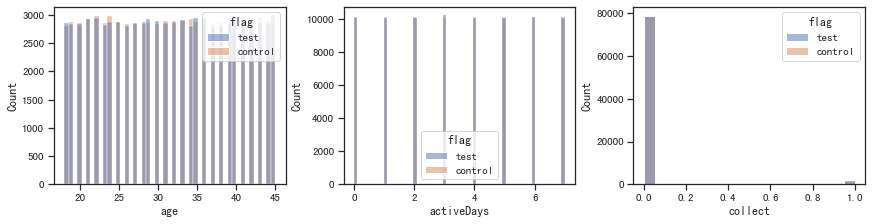
# 查看连续变量的分布
fig, ax =plt.subplots(1, 3, constrained_layout=True, figsize=(12, 3))
for i, x in enumerate(['age', 'activeDays', 'collect']):
    sns.histplot(x=x, data=df, hue='flag', ax=ax[i])
plt.show()

# 检验样本比例一致性
n1=control.size
n2=test.size
p1=p2=0.5
two_sample_proportion_test(n1, n2, p1, p2)

两样本比例校验: 通过

• 样本特征一致性校验

# 检验特征分布一致性
cols=['cityLevel', 'gender', 'device', 'age', 'activeDays']
feature_dist_ks(cols, test, control)

cityLevel: 相似
gender: 相似
device: 相似
age: 相似
activeDays: 相似

• 显著性检验

# 显著性检验
count1=test['collect'].sum()
nobs1=test['collect'].size
count2=control['collect'].sum()
nobs2=control['collect'].size

prob_cal_significant(count1, nobs1, count2, nobs2)

(3.8761435754191123,
 0.00010612507775057984,
 [0.0013796298310413291, 0.004202600259759636])

• p值小于5%，置信区间不包含0。因此整体上可以认为此次优化有助于提高【把喜欢的音乐加入收藏夹】功能的使用率。
• 但是需要注意置信区间最小提升为0.0014，而在自然波动的最大提升是0.0019（0.0219-0.02），所以此次提升有可能在自然波动范围内，可能存在业务不显著，需要额外关注。

• 拓展-维度下钻分析

# 进行维度下钻分析，采用BH法进行多重检验校正
feature=[]
value=[]
pvaules=[]
for x in ['cityLevel', 'gender', 'device']:
    for i in df[x].unique():
        feature.append(x)
        value.append(i)
        # 构造细分维度的样本
        te=test[test[x]==i]
        co=control[control[x]==i]
        # 计算细分维度的p值
        c1=te['collect'].sum()
        n1=te['collect'].size
        c2=co['collect'].sum()
        n2=co['collect'].size
        p=prob_cal_significant(c1, n1, c2, n2)[1]
        pvaules.append(p)
    
df_multiple=pd.DataFrame({'feature':feature,
                        'value':value,
                        'pvaules':pvaules
                       })
df_multiple

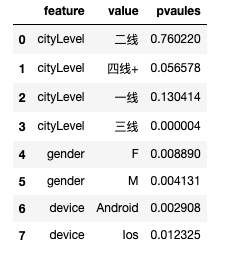
# 多重检验校正
print(multiple_tests_adjust(df_multiple['pvaules']))
df_multiple['pvaules_correct']=multiple_tests_adjust(df_multiple['pvaules'])[1]
df_multiple['reject']=multiple_tests_adjust(df_multiple['pvaules'])[0]
df_multiple

(array([False, False, False,  True,  True,  True,  True,  True]), array([7.60220226e-01, 7.54367218e-02, 1.49044597e-01, 3.53217899e-05,
       1.77798888e-02, 1.10151024e-02, 1.10151024e-02, 1.97199451e-02]), 0.00625)

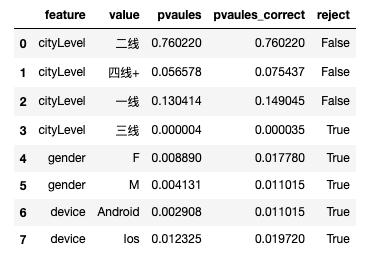
维度下钻发现，一线、二线和四线+城市提升不显著

实验报告

# 关键数据展示

# 样本及均值
print('control:' ,f'sample {control.shape[0]} / mean:{control.collect.mean()}')
print('test:' ,f'sample {test.shape[0]} / mean:{test.collect.mean()}')
# 实验周期
print('times:', test_time)
# diff
print('diff:', test['collect'].mean()-control['collect'].mean())
# p值
print('p-value:', prob_cal_significant(count1, nobs1, count2, nobs2)[1])
# diff-置信区间
print('diff-ci:', prob_cal_significant(count1, nobs1, count2, nobs2)[2])
# 维度下钻结果
print('dim-result:')
for i,v in zip(df_multiple.value,df_multiple.reject):
    print(' '*2,f'{i}:{v}')

control: sample 80640 / mean:0.019952876984126983
test: sample 80640 / mean:0.022743055555555555
times: 10
diff: 0.002790178571428572
p-value: 0.00010612507775057984
diff-ci: [0.0013796298310413291, 0.004202600259759636]
dim-result:
   二线:False
   四线+:False
   一线:False
   三线:True
   F:True
   M:True
   Android:True
   Ios:True

• 实验10天，收集到实验组数据80640，对照组80640，共计161280。
• 实验过程无异常，实验组人均收藏率为0.023，较对照组提高0.003
• 整体上，实验组的提升是显著的，且提升范围在[0.001, 0.004]之间。但可能存在业务不显著，需要额外关注
• 通过维度下钻，发现实验组在一线、二线和四线+城市提升不显著

总结

现在，关于均值类和概率类的所有实验细节和模拟实战都已结束，相信大家对如何科学地进行A/B试验已经了然于胸了吧～

共勉～