目录
目录结构
ls
cd
stat
touch
mkdir
whoami 查看当前帐号是谁

who 查看当前有哪些人在使用

pwd 当前的工作目录

目录结构
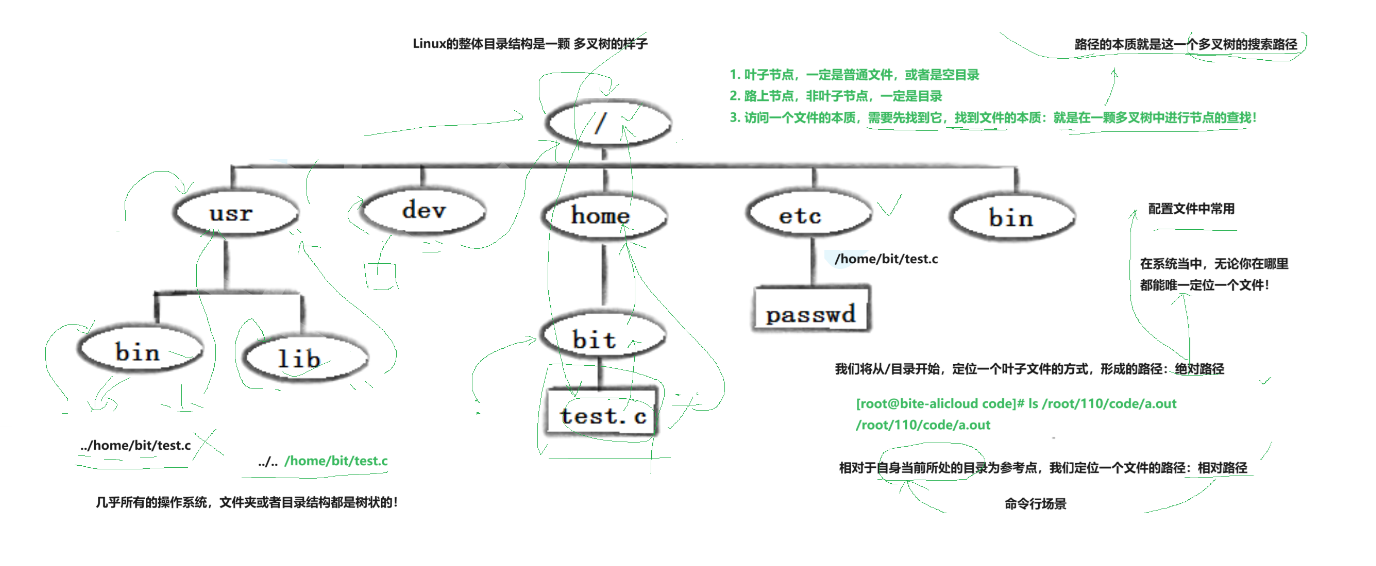
目录结构就是一颗多叉树的样子
路径
![]()
我们从 / 目录开始,定位一个叶子文件的方式,形成的路径称为:绝对路径
我们从当前位置开始,定位一个文件的路径称为:相对路径

ls
ls 查看当前目录下的文件信息

ls -l == ll 查看当前目录下的文件信息,-l 显示文件属性

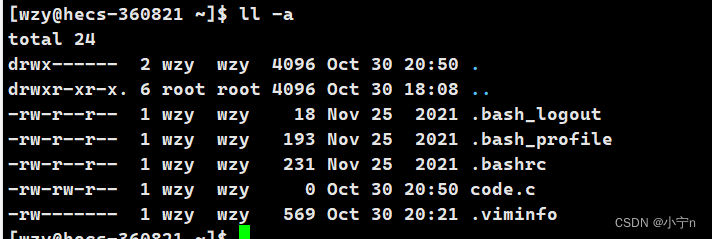
ls -a 显示当前目录下的隐藏文件
隐藏文件在linux中常以 . 开头

ll -a 显示当前目录下的所有文件(包括隐藏文件)
cd
cd命令: cd相对路径或者绝对路径
cd ~ 家目录:用户登陆时的目录称为家目录
cd - 跳转回最近一次所处的目录
cd .. 回到上级目录
stat
查看文件更详细的信息
Access :最后一次读取的时间(访问)
Modfiy :最后一次数据的时间(修改)
Change : 最后一次修改数据权限的时间(改变)

touch
touch +文件名 创建一个普通文件
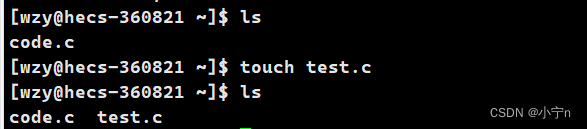
创建一个隐藏文件,在文件名前加 .
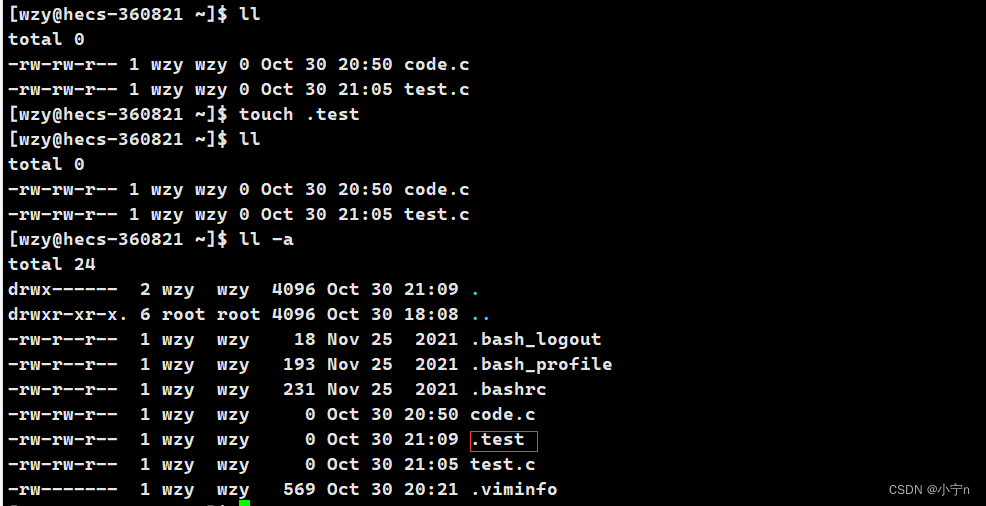
mkdir
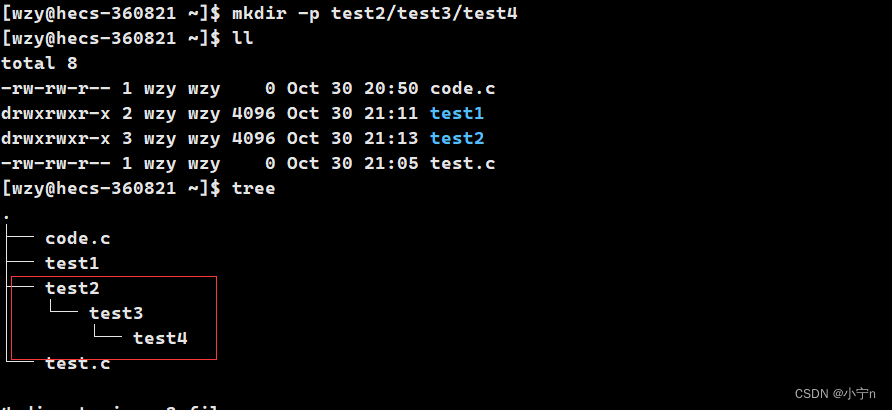
mkdir + 目录名 创建一个目录
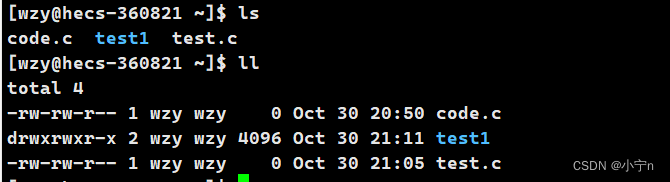
mikdir -p d1/d2/d3/d4 创建一个多级目录