论文:https://arxiv.org/abs/2011.14141
代码:https://github.com/open-mmlab/mmsegmentation/tree/main/projects/Adabins
0、摘要
本文主要解决了从单个RGB输入图像估计高质量密集深度图的问题。我们从一个baseline的encoder-decoder CNN结构出发,提出一个问题:信息的全局处理如何帮助提高整体深度估计?为此,我们提出了一种基于transformer的架构块,它将深度范围划分为多个 bin,而每个bin的中心值是根据每个图像自适应估计的,最终的深度值估计为 bin 中心的线性组合。我们将这种新的构造块称为AdaBins。我们的结果显示,在所有指标上,在几个流行的深度数据集上都比现有技术有了决定性的改进。我们还通过消融研究验证了所提出的块的有效性,并提供了新的最先进模型的代码和相应的预训练权重。
1、引言
本文解决了从单个RGB输入图像估计高质量密集深度图的问题。这是计算机视觉中的一个经典问题,对许多应用至关重要。在这项工作中,我们提出了一种新的架构构建块,称为AdaBins,它为在两个最流行的室内和室外数据集NYU和KITTI上进行深度估计带来了一种最先进的新架构。
我们工作的动机是猜测当前的体系结构没有对输出值进行足够的全局分析。卷积层的一个缺点是,只有当张量在瓶颈处或瓶颈附近达到非常低的空间分辨率时,它们才会处理全局信息。然而,我们相信,在高分辨率下进行全局处理会更加强大。我们的总体想法是对传统编码器-解码器架构的输出执行全局统计分析,并使用以最高分辨率操作的训练过的后处理构建块来细化输出。作为这种思想的一种特殊认识,我们提出分析和修改深度值的分布。
与不同RGB输入相对应的深度分布可以在很大范围内变化(见图1)。一些图像的大多数对象位于非常小的深度值范围内。比如,家具特写图像中包含大部分靠近相机的像素,而其他图像则具有分布在更宽范围上的深度值,比如走廊,深度值的范围从很小的值到网络支持的最大深度值。随着问题的不适定性,深度分布的这种变化使得以端到端的方式进行深度回归变得更加困难。最近的工作已经提出利用关于室内环境的假设,如平面性约束,来指导网络,这可能适用也可能不适用于真实世界的环境,尤其是室外场景。
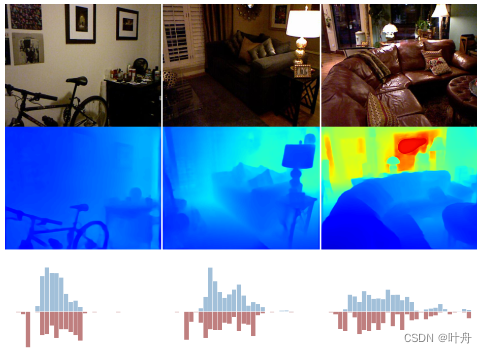
我们没有基于这样的假设继续研究,而是提出了一种新方法,在该方法中,网络学会自适应地关注深度范围内更可能出现在输入图像场景中的区域。
主要贡献如下:
- 提出了一个可以执行场景信息全局处理的构造块,提出将预测的深度范围划分为每个图像的宽度可变的bins。最终的深度估计是bin中心值的线性组合。
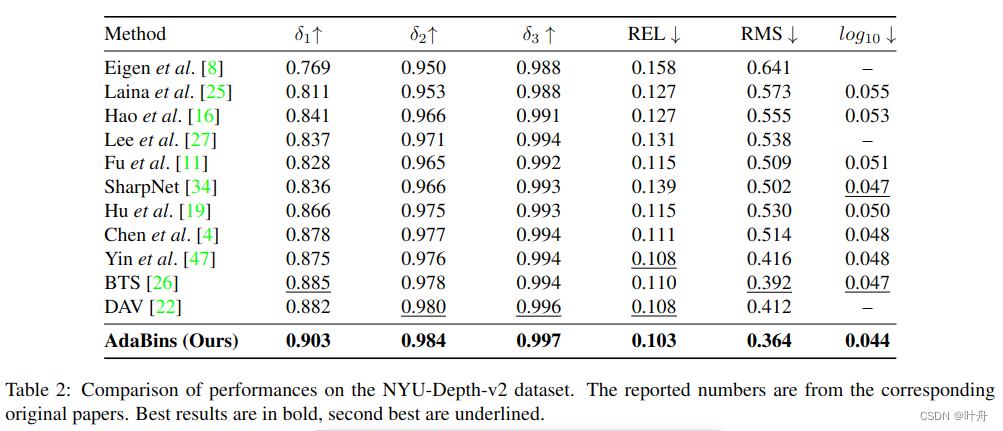
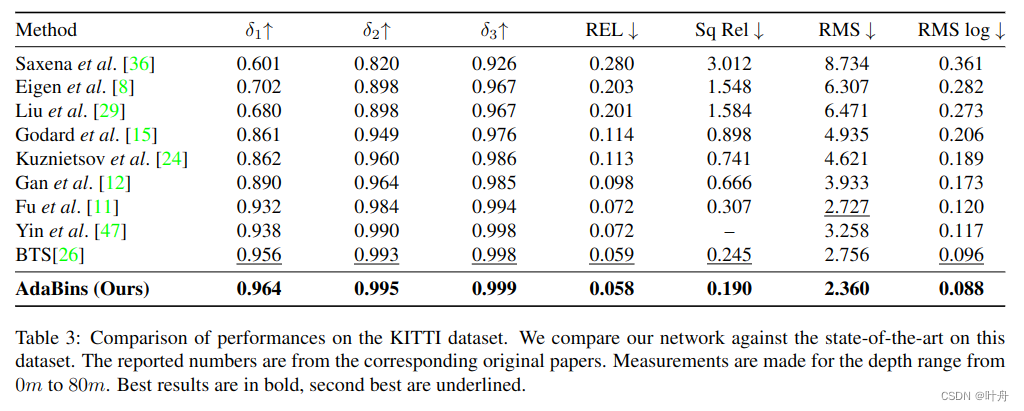
- 在两个最流行的数据集NYU和KITTI的所有指标中,显示了监督单图像深度估计的决定性改进。
- 我们分析了我们的发现,研究了对所提出的AdaBins块的不同修改,并研究了它们对深度估计准确性的影响。
2、相关工作
从RGB图像重建三维场景的问题是一个不适定问题。缺乏场景覆盖、比例模糊、半透明或反射材质等问题都会导致无法从外观中导出几何体的模糊情况。最近,依赖卷积神经网络(CNNs)的方法能够以实时速度从单个RGB输入图像中生成合理的深度图。
单目深度估计(Monocular depth estimation)已经被许多CNN方法认为是从单个RGB图像中的密集深度图的回归。
我们考虑了两个最接近我们方法的工作:BTS和DAV。BTS在解码阶段使用局部平面引导层来将特征引导到全分辨率,而不是标准上采样层。DAV使用标准的编码器-解码器方案,并提出通过关注bottleneck来利用场景中对象的共面性。
编码器-解码器网络在许多与视觉相关的问题上做出了重大贡献,如图像分割[35]、光流估计和图像恢复。近年来,这种架构的使用在深度估计问题的有监督和无监督设置中都取得了巨大成功。这种方法通常使用一个或多个编码器-解码器网络作为其较大网络的子部分。在本文中,我们采用了《High Quality Monocular Depth Estimation via Transfer Learning》使用的baseline编码器网络架构。这使我们能够更明确地研究我们提出的管道扩展的性能归因,这通常是一项困难的任务。
transformer网络作为一种可行的构建块,在NLP任务和计算机视觉任务中的传统使用之外,正受到越来越多的关注。继最近将CNN与Transformer相结合的趋势取得成功之后,我们建议利用Transformer编码器作为CNN输出的non-local处理的构建块。
3、方法
在本节中,我们介绍了这项工作的动机,提供了AdaBins架构的细节,并描述了相应的损失函数的使用。
3.1. 动机
我们的想法可以被视为通过有序回归网络对深度估计的推广,如Fu等人提出的那样,他们观察到,如果将深度回归任务转换为分类任务,则可以实现性能改进,他们建议将深度范围划分为固定数量的预定宽度的bins。我们的推广解决了初始方法的多个局限性。首先,我们提出计算根据输入场景的特征动态变化的自适应bin。其次,分类方法导致深度值的离散化,这导致视觉质量差,具有明显的尖锐深度不连续性。这可能仍然会得到关于标准评估指标的较好结果,但它可能会对下游应用提出挑战,例如计算摄影或3D重建。因此,我们建议将最终深度值预测为bin中心的线性组合。这使我们能够将分类的优势与深度图回归的优势相结合。最后,与其他架构(例如DAV)相比,我们以高分辨率全局的计算信息,而不是在低分辨率的瓶颈部分计算信息。
3.2. AdaBins设计
我们讨论了我们提出的架构的四种设计选择,这些选择对获得的结果最重要。
首先,我们采用自适应分仓策略将深度区间D=(dmin,dmax)离散为N个bin。对于给定的数据集,此间隔是固定的,并由数据集规范确定或手动设置为合理的范围。为了说明我们将深度区间划分为区间的想法,我们想将我们的最终解决方案与我们评估的其他三种可能的设计选择进行对比:
- 具有均匀bin宽的固定bin:深度间隔D被划分为大小相等的N个bin;
- 具有对数刻度bin宽度的固定bin:深度间隔D按对数刻度划分为大小相等的bin;
- 训练过的bin宽度:bin宽度是自适应的,可以针对特定的数据集进行学习。由于bin宽度是通用的,因此所有图像最终共享深度间隔D的相同bin;
- AdaBins:为每个图像自适应地计算bin宽度;
我们推荐AdaBins策略作为最佳选择,我们的消融研究通过显示该设计相对于其替代方案的优势来验证这一选择。bin宽度的四种设计选择如图3所示。
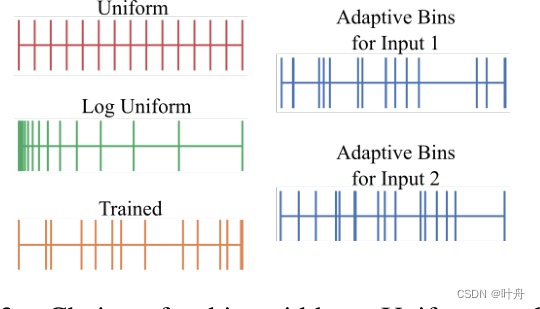
其次,将深度间隔D离散化为多个bin,并将每个像素分配到一个单独的bin中,这导致了深度离散化伪影。因此,我们将最终深度预测为仓中心的线性组合,从而使模型能够估计平滑变化的深度值。
第三,一些前期工作(图像字幕、目标检测等)提出在encoder块之后使用注意力模块来进行全局处理。此外,当前的SOTA深度估计使用了这种策略,这样的体系结构由三个块组成,按顺序排列:编码器、注意力,然后是解码器。我们最初遵循了这种方法,但考虑到在空间上更高分辨率的feature map上使用注意力可以获得更好的结果。因此,我们提出了一种架构,它也有这三个块,但顺序如下:编码器、解码器,最后是注意力。
第四,我们希望建立在尽可能简单的架构上,以强调我们新提出的AdaBins概念的影响。因此,我们在现代编码器的基础上构建编码器,使用EfficientNet B5作为编码器的主干。
在下一小节中,我们将对整个体系结构进行描述。
3.3. 体系结构描述
图2显示了我们提出的深度估计架构的概述。我们的架构由两个主要组件组成:1)建立在预训练的EfficientNet B5[40]编码器和标准特征上采样解码器上的编码器-解码器块;2) 我们提出的自适应bin宽度估计器块称为AdaBins。第一个组成部分主要基于Alhashim和Wonka的简单深度回归网络,并进行了一些修改。两个基本的修改是:从DenseNet改为EfficientNet B5,并为新架构使用不同的损失函数。此外,解码器的输出是张量,而不是表示最终深度值的单通道图像,我们将这个张量称为“decoded features”。第二个组件是本文的一个关键贡献,AdaBins模块。AdaBins模块的输入是大小为h×w×Cd的解码特征,输出张量的大小为h x w×1。由于当前GPU硬件的内存限制,我们使用h=H/2和w=W/2来使用更大的batch size,然后通过简单的双线性上采样到H×W×1来计算最终的深度图。
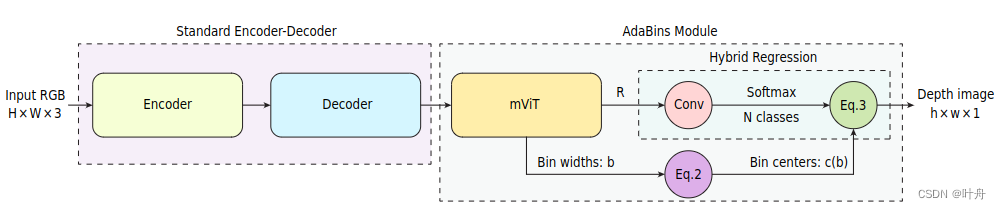
AdaBins模块中的第一个块称为miniViT,该块的概述如图4所示。它是ViT的一个简化版,并做了微小改动。mini-ViT有两个输出:1)bin度的矢量b,它定义了如何为输入图像划分深度间隔D;2)大小为h×w×C的范围注意力映射R,它包含像素级深度计算的有用信息。

Mini-ViT: 估计深度范围D内对于给定图像更有可能发生的子区间将需要同时组合局部结构信息和全局分布信息。我们建议使用全局注意力来计算每个输入图像的bin宽度向量b。全局注意力在内存和计算复杂性方面都是昂贵的,尤其是在更高分辨率下。然而,最近transformer的快速发展提供了一些有效的替代方案。我们在设计带有transformer的AdaBins模块时,从Vision Transformer ViT中获得了灵感。我们还使用了一个小得多的transformer版本,因为我们的数据集更小,并在以下描述中将此transformer称为mini-ViT或mViT。
Bin-widths:我们首先描述如何使用mViT来获得bin宽度向量b。mViT块的输入是解码特征的张量。然而,transformer采用一系列固定大小的矢量作为输入。我们首先将解码的特征通过卷积块,称为嵌入卷积(见图4),核大小为p×p,步长为p,输出通道数为E。因此,这个卷积的结果是大小为h/p×w/p×E的张量(假设h和w都可以被p整除)。其结果中空间维度被拉平,形成向量
,其中S=hw/p^2作为transformer的有效序列长度。我们将这个E维向量序列称为patch嵌入。
根据常见操作,我们在将patch嵌入送到transformer之前,将学习的位置编码添加到patch嵌入中。我们的transformer是一个小型transformer(详见表1),并输出一系列输出嵌入。我们在第一个输出嵌入上使用了MLP头(我们还试验了一个版本,该版本有一个额外的特殊令牌作为第一个输入,但没有看到改进)。MLP头使用ReLU激活并输出N维矢量b′。最后,我们对向量b′进行归一化,使其总和为1,以获得如下的bin宽度向量b:
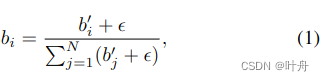
式中,较小的正值可以确保每个bin宽度严格非负。归一化引入了bin宽度之间的竞争,并通过预测D的感兴趣区域的较小仓宽度,在概念上迫使网络关注D内的子区间。
在下一小节中,我们将描述如何从解码的特征和transformer输出嵌入中获得范围注意力映射R。
Range attention maps:在这一点上,解码的特征表示高分辨率的局部像素级信息,而transformer的输出嵌入有效地包含更多的全局信息。如图4所示,来自transformer的输出嵌入第2到C+1的部分被用作1×1卷积核,并且与解码的特征进行卷积(后接3×3卷积层)以获得范围注意力映射R。这相当于计算被视为“keys”的像素特征和被视为‘queries’的transformer输出嵌入之间的点积注意力权重。这种使用输出嵌入作为卷积核的简单设计允许网络将来自transformer的自适应全局信息集成到解码特征的局部信息中。R和b被一起使用以获得最终的深度图。
Hybrid regression:距离-注意力映射R通过1×1卷积层获得N个通道,然后进行Softmax激活。我们将N个Softmax得分pk,k=1...N解释为根据bin宽度向量b计算的N个深度bin中心c(b):={c(b1),c(b2),…,c(bN)}上的概率。bin宽度向量为:
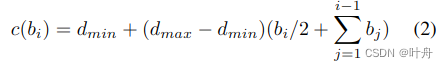
最后,在每个像素处,根据该像素处的Softmax分数和深度bin中心c(b)的线性组合计算最终深度值,如下所示:

与Fu等人相比,我们没有直接将深度预测为最有可能的bin的bin中心。这使我们能够在没有离散化伪影的情况下预测平滑的深度图,如图5所示:

3.4. 损失函数
Pixel-wise depth loss:们使用了Eigen等人引入的比例不变损失(SI)的缩放版本:
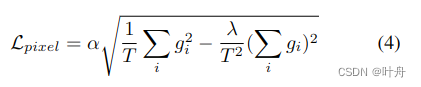
其中,GT深度
和 T表示具有有效GT值的像素的数量。我们在所有实验中使用λ=0.85和α=10。
Bin-center density loss: 该损失项鼓励bin中心的分布遵循GT中深度值的分布。我们希望鼓励bin中心接近GT深度值,反之亦然。我们将bin中心的集合表示为c(b),将GT图像中所有深度值的集合表示为由X,并使用双向切角损失作为正则化子:
![]()
最终,总的损失为:
![]()
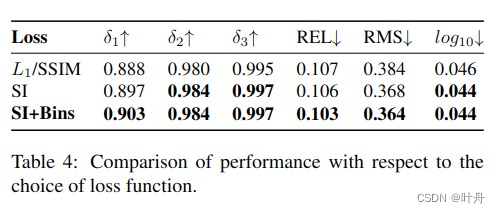
我们为所有实验设置了β=0.1。我们对不同的损失函数进行了实验,包括RMSE损失,以及[1]提出的组合SSIM加L1损失。然而,我们能够通过我们提出的损失获得最佳结果。我们在消融研究中对不同的损失函数及其性能进行了比较。
4、实验结果


5、结论
我们引入了一个新的架构块,称为AdaBinsfor,用于从单个RGB图像进行深度估计。AdaBins在NYU和KITTI这两个最受欢迎的数据集上,相比之前的SOTA取得了决定性的提升。在未来的工作中,我们希望研究高分辨率信息的全局处理是否也能提高其他任务的性能,如分割、法线估计和多幅图像的3D重建。