A Gentle Introduction to Graph Neural Networks
A Gentle Introduction to Graph Neural Networks
GNN简介
图神经网络(GNN)是一种基于图结构数据的深度学习模型,用于处理和分析图数据。图数据由节点(顶点)和边(连接节点的线)组成,它们可以表示为社交网络、推荐系统、生物信息学中的分子结构等。
简介: GNN是一种利用节点和节点之间关系的信息进行学习的模型。与传统的深度学习模型不同,GNN考虑了节点的邻居节点的信息,使得节点可以通过邻居节点的信息进行信息传播和学习。这种模型结构使得GNN在处理图结构数据时非常有效。
重要性: GNN的重要性在于其对非结构化数据(如图数据)进行建模和学习的能力。它扩展了深度学习的范畴,使得能够处理更加复杂的数据结构,并在许多领域取得了重要的成果。GNN能够学习节点间的复杂关系,从而可以用于预测、分类、聚类等任务。
应用领域: GNN在多个领域有着广泛的应用,包括但不限于:
-
社交网络分析: 用于发现社交网络中的社区结构、影响力分析、推荐系统等。
-
推荐系统: 基于用户行为数据和物品关系图,提高个性化推荐的准确性。
-
生物信息学: 分析蛋白质相互作用、药物发现、基因表达等方面,有助于发现模式和相互关系。
-
金融领域: 用于风险管理、欺诈检测和市场预测等,分析复杂的金融交易关系。
-
物联网(IoT): 处理物联网中设备之间的连接和关系,优化网络管理和资源分配。
-
推荐系统: 用于电子商务中的个性化推荐、新闻推荐等领域,结合用户行为和物品关系。
这些仅仅是一些典型的应用领域,随着研究的深入,GNN在更多领域中的应用也在不断扩展。
图的基本组成
图是由节点(或顶点)和边(或连接)组成的一种抽象数学结构。这两个基本组成部分定义了图的基本元素和它们之间的关系。以下是图的基本组成部分:

-
节点(顶点): 节点是图中的基本单元,通常用来表示实体或对象。在图中,节点可以是任何东西,比如一个人的社交网络中的个人、一篇文章、一个城市等。节点用来表示图中的各种实体,有时也带有属性或特征。
-
边(连接): 边是节点之间的连接,用来表示节点之间的关系。边可以是有向的(箭头指示连接的方向)或无向的(连接没有指定方向)。边也可以有权重,表示节点之间连接的强度或相关性。在社交网络中,边可以表示两个人之间的关系,比如朋友关系。
-
图的属性: 图还可以有一些属性,比如图的类型(有向图、无向图)、规模(节点数量、边的数量)、密度(实际边数和可能边数的比例)、连通性等。
总的来说,图由节点和边组成,它们之间的连接关系描述了实体之间的关联或联系。图可以以各种形式出现,并且在不同领域中有着广泛的应用。
GNN可以做什么
为了进一步描述每个节点、边或整个图,我们可以在图的每个部分中存储信息。
利用图神经网络的目的就是整合特征!

图像作为图表:我们通常将图像视为具有图像通道的矩形网格,将它们表示为数组(例如,244x244x3 浮点数)。另一种将图像视为具有规则结构的图,其中每个像素代表一个节点,并通过边缘连接到相邻像素。每个非边界像素正好有 8 个邻居,每个节点存储的信息是表示该像素的 RGB 值的 3 维向量。
可视化图的连通性的一种方法是通过其邻接矩阵。我们对节点进行排序,在本例中,每个节点是一个简单的 5x5 笑脸图像中的 25 个像素,并填充一个矩阵N*N如果两个节点共享一条边,则有一个条目。请注意,下面这三种表示形式都是同一数据的不同视图。
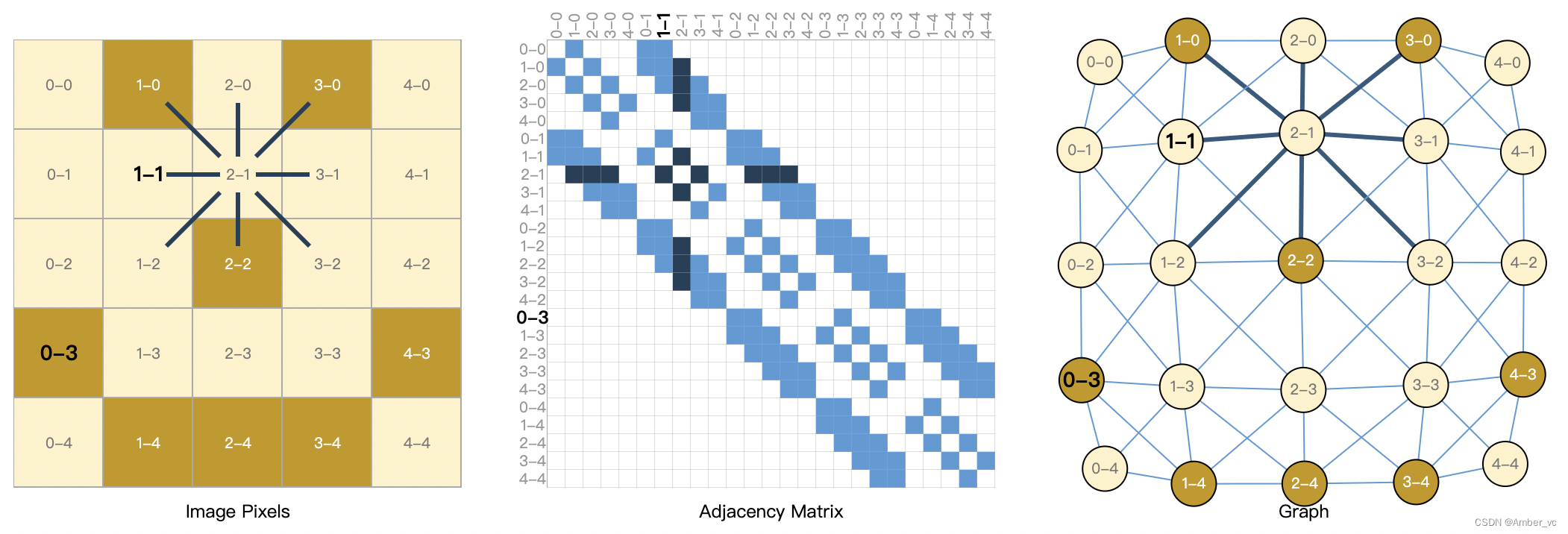
文本作为图表:我们可以通过将索引与每个字符、单词或标记相关联,并将文本表示为这些索引的序列来数字化文本。这将创建一个简单的有向图,其中每个字符或索引都是一个节点,并通过边连接到其后面的节点。

当然,在实践中,这通常不是文本和图像的编码方式:这些图形表示是多余的,因为所有图像和所有文本都将具有非常规则的结构。例如,图像的邻接矩阵具有带状结构,因为所有节点(像素)都连接在网格中。文本的邻接矩阵只是一条对角线,因为每个单词仅连接到前一个单词和下一个单词。
用邻接矩阵A表示邻居之间的关系
GNN的主要任务: Graph级别的任务
在图级任务中,我们的目标是预测整个图的属性。
like:分子结构

GNN的主要任务: Node级别的任务
节点级任务涉及预测图中每个节点的身份或角色。
like:社交网络

构建GNN
1、构建图。第一步是考虑如何表示与神经网络兼容的图。
邻接矩阵的缺点:
1)节点数量可能约为数百万,并且每个节点的边数可能变化很大。通常,这会导致邻接矩阵非常稀疏,空间效率低下。
2)有许多邻接矩阵可以编码相同的连接性,并且不能保证这些不同的矩阵在深度神经网络中会产生相同的结果(也就是说,它们不是排列不变的)。
表示稀疏矩阵的一种优雅且节省内存的方式是邻接表。如下:
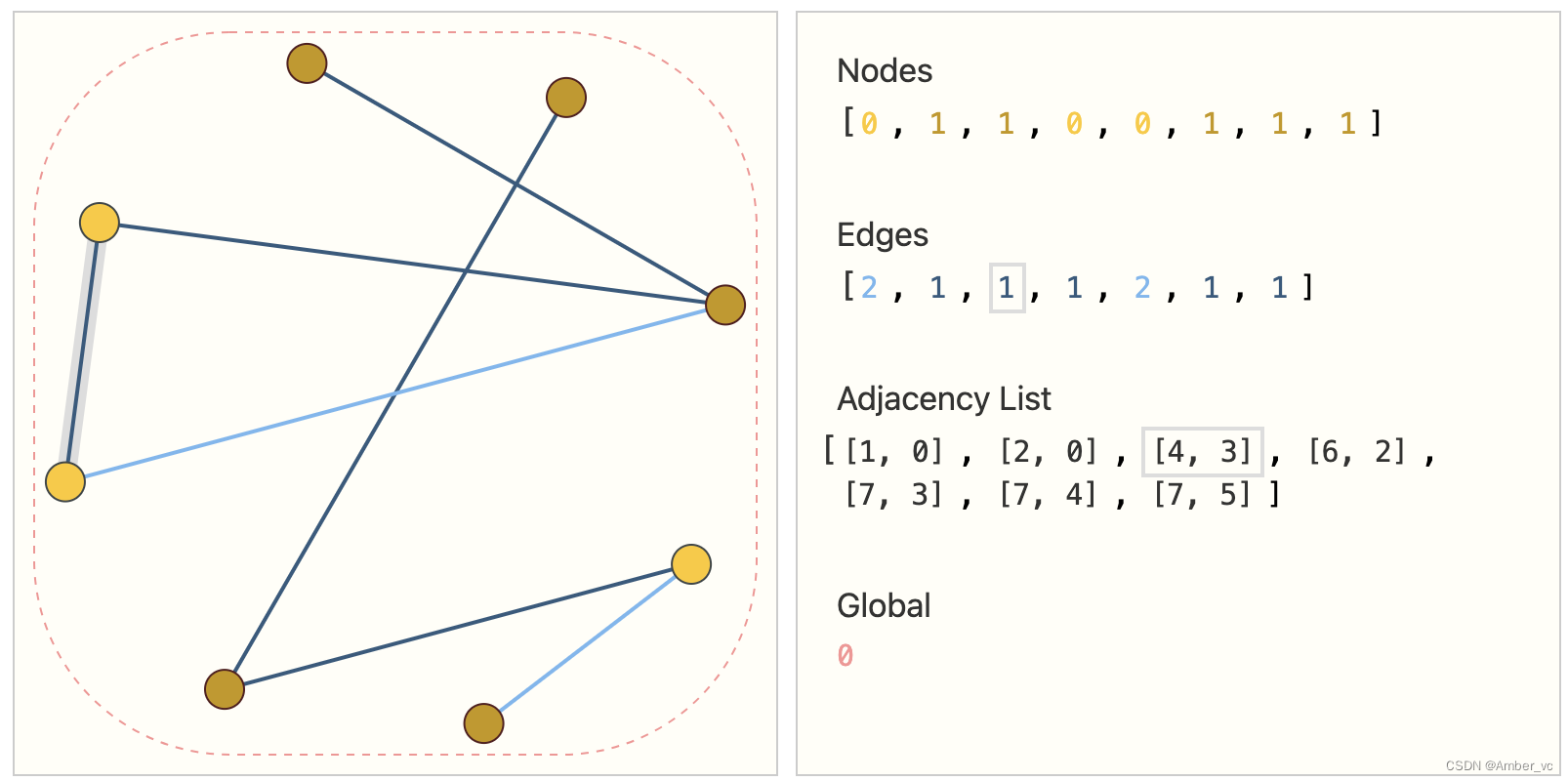
GNN 是对图的所有属性(节点、边、全局上下文)的可优化变换,可保留图对称性(排列不变性)。
该GNN 在图的每个组件上使用单独的多层感知器 (MLP);我们称之为 GNN 层。对于每个节点向量,我们应用 MLP 并获取学习到的节点向量。我们对每条边执行相同的操作,学习每条边的嵌入,并且对全局上下文向量执行相同的操作,学习整个图的单个嵌入。
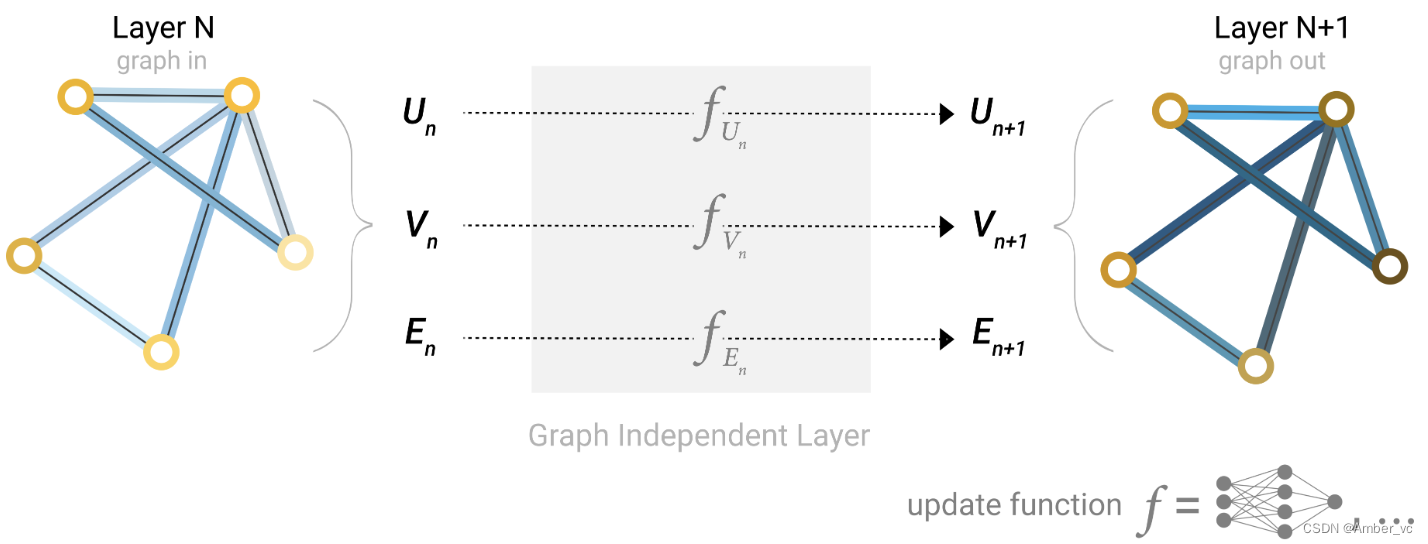
与神经网络模块或层一样,我们可以将这些 GNN 层堆叠在一起。
由于 GNN 不会更新输入图的连通性,因此我们可以使用与输入图相同的邻接表和相同数量的特征向量来描述 GNN 的输出图。但是,输出图已经更新了嵌入,因为 GNN 已经更新了每个节点、边和全局上下文表示。
2、消息传递
消息传递分三个步骤进行:
-
1)对于图中的每个节点,收集所有相邻节点的嵌入(或消息)。
-
2)通过聚合函数(如 sum)聚合所有消息。
-
3)所有汇集的消息都通过更新函数(通常是学习的神经网络)传递。

信息聚合:聚合操作可以当作全连接层。
但是更新的方法有很多,可以自己设置:(与CNN相似)
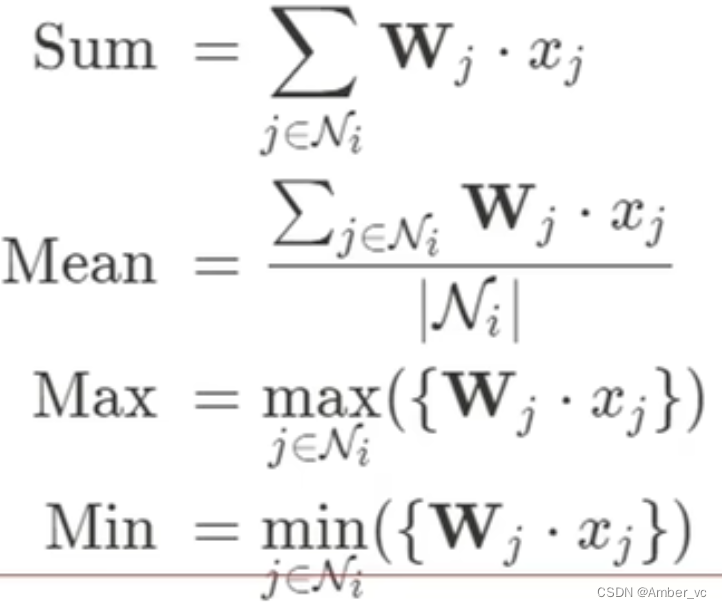

信息更新:每个点的特征该如何更新呢? 考虑自身信息+邻居信息
结合自身与邻居信息:![]()
汇总: ![]()
更新后 = 激活函数(自己的信息+邻居特征)
ps: GNN也可以有多层,GNN的本质就是更新各部分特征

其中输入是特征,输出也是特征,邻接矩阵也不会变的
3、最后预测
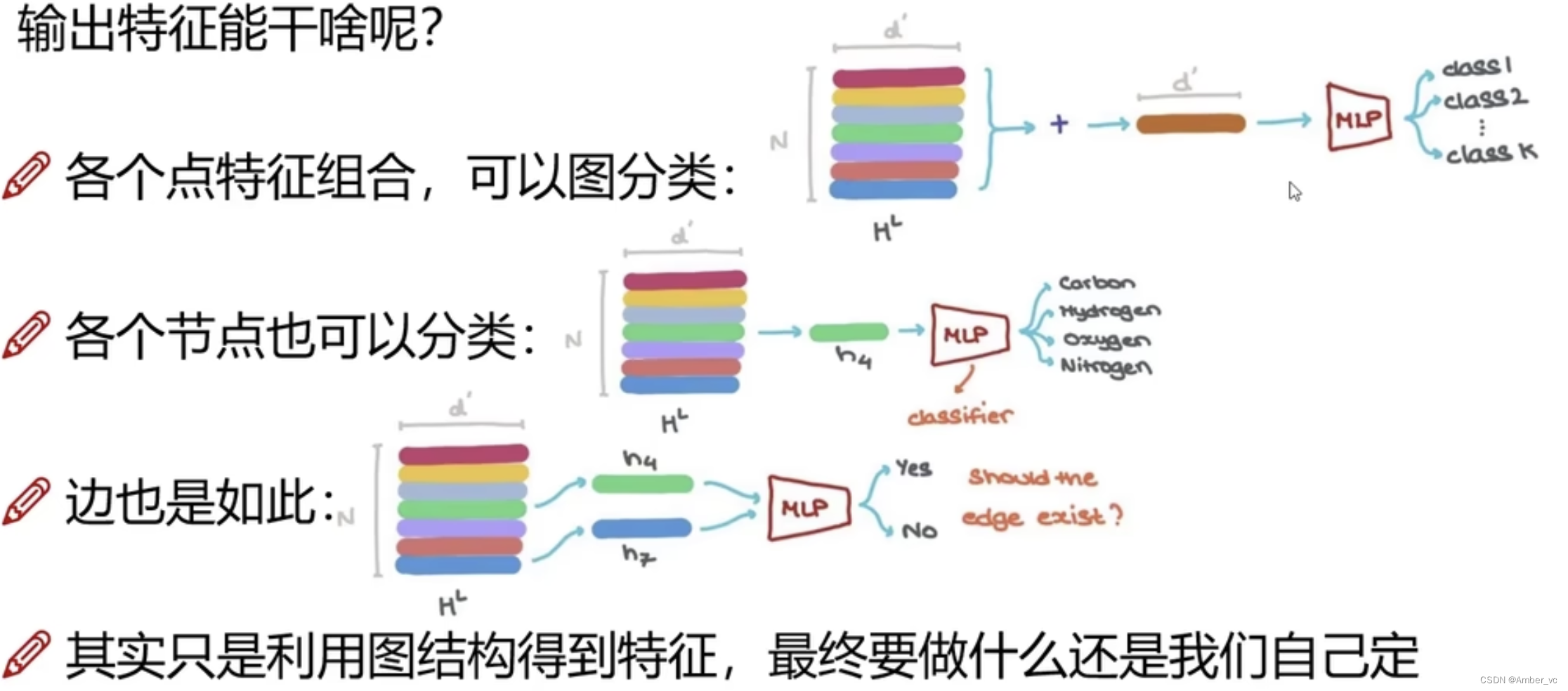
我们已经构建了一个简单的 GNN,但是我们如何在上面描述的任何任务中进行预测呢?
我们将考虑二元分类的情况,但该框架可以轻松扩展到多类或回归情况。如果任务是对节点进行二进制预测,并且图已经包含节点信息,则方法很简单 - 对于每个节点嵌入,应用一个线性分类器。

然而,事情并不总是那么简单。例如,您可能在图中存储了边中的信息,但在节点中没有信息,但仍然需要对节点进行预测。我们需要一种从边缘收集信息并将其提供给节点进行预测的方法。我们可以通过池化来做到这一点。池化分两步进行:
-
1)对于要合并的每个项目,收集它们的每个嵌入并将它们连接成一个矩阵。
-
2)然后,通常通过求和运算来聚合收集到的嵌入。
-
因此,如果我们只有边缘级特征,并且尝试预测二进制节点信息,我们可以使用池化将信息路由(或传递)到需要去的地方。模型看起来像这样。
-
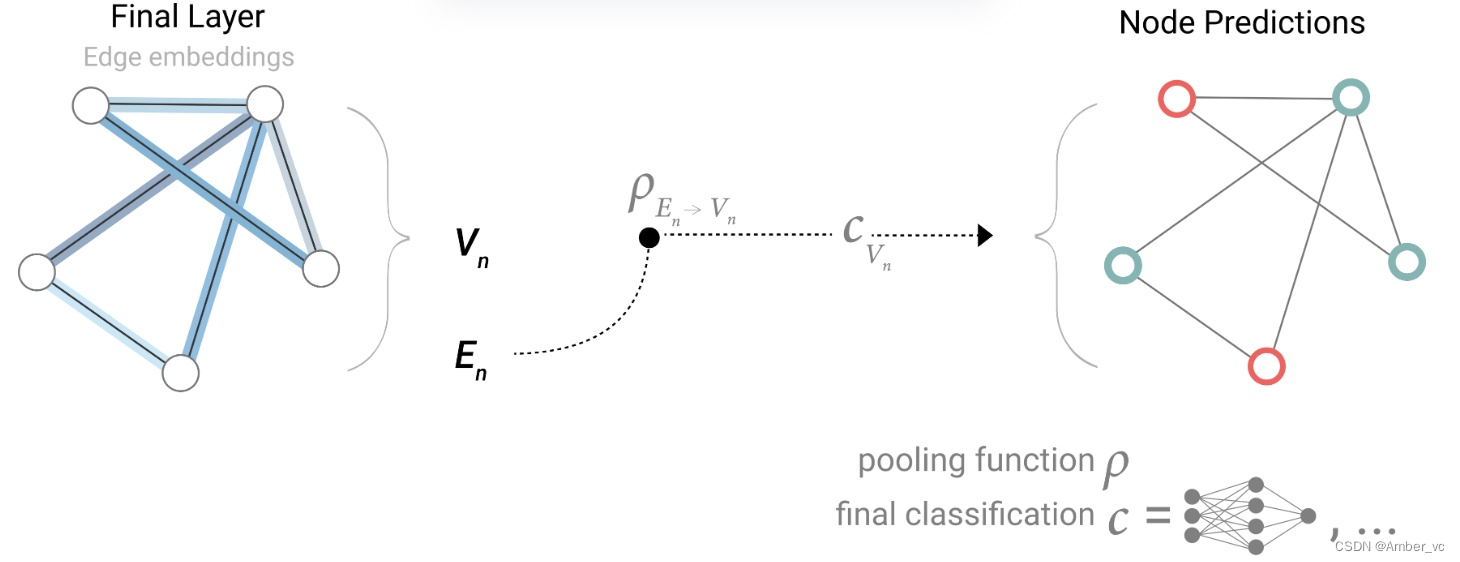
如果我们只有节点级特征,并尝试预测二进制边缘级信息,则模型如下所示。
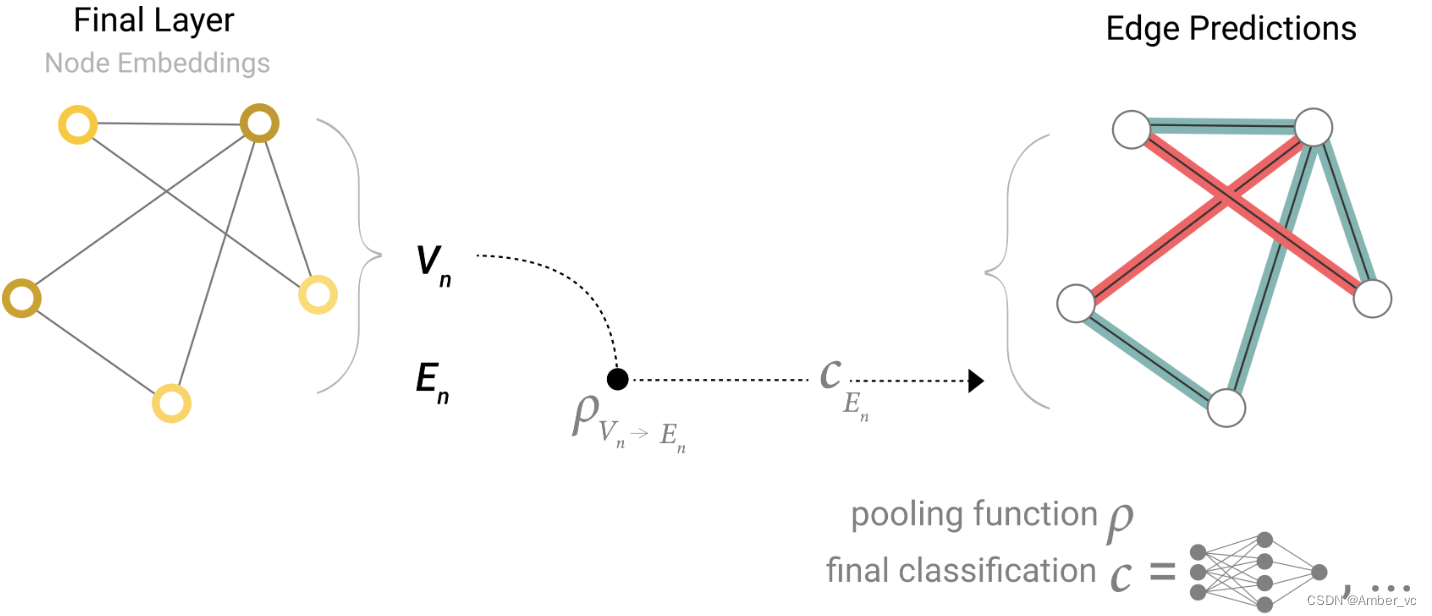
如果我们只有节点级特征,并且需要预测二元全局属性,则需要将所有可用的节点信息收集在一起并聚合它们。这类似于CNN 中的全局平均池层。对于边缘也可以进行同样的操作。
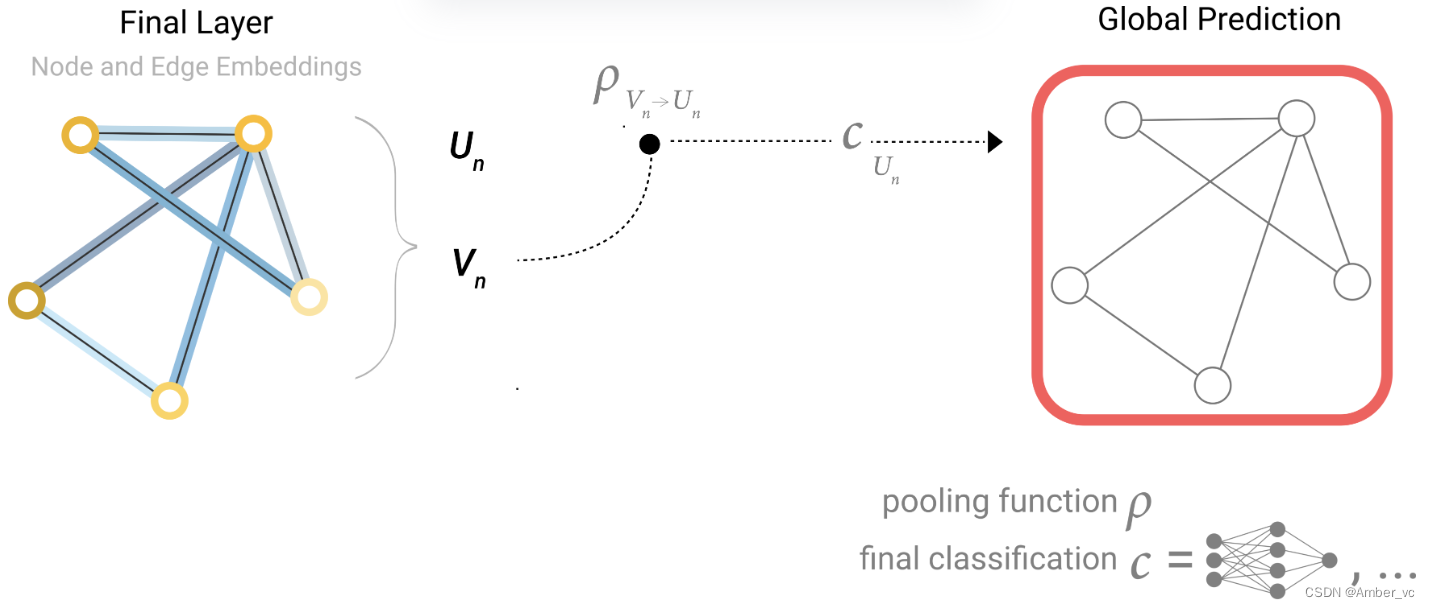
请注意,在这个最简单的 GNN 公式中,我们根本没有在 GNN 层内使用图的连接性。每个节点、每条边以及全局上下文都是独立处理的。我们仅在汇集信息进行预测时使用连接性。