文章目录
- 前言
- 一、OOK
- 1、表达式
- 2、功率谱密度
- 3、调制框图
- 二、2PSK
- 1、表达式
- 2、功率谱密度
- 三、2FSK
- 1、表达式
- 四、MATLAB 仿真
- 1、MATLAB 源码
- 2、仿真及结果
- ①、输入信号及频谱图
- ②、2ASK 调制
- ③、2PSK 调制
- ④、2FSK 调制
- ⑤、随机相位 2FSK 调制
- 五、资源自取
前言
数字频带信号通常也称为数字调制信号,其信号频谱通常是带通型的,适合于在带通型信道中传输。数字调制是将基带数字信号变换成适合带通型信道传输的一种信号处理方式,正如模拟通信中的一样,可以通过对基带信号的频谱搬移来适应信道特性,也到同样的目的可以采用频率调制、相位调制的方式来达到同样的目的。
本文将主要通过 Matlab 来学习二进制的调制解调方式,包括 OOK、2PSK、2FSK,并分析和仿真这些调制系统。
一、OOK
1、表达式
如果将二进制码元 “0” 对应信号 0,“1” 对应信号
A
c
o
s
2
π
f
c
t
Acos2\pi f_ct
Acos2πfct,则 OOK 信号可以写成如下表达式:
s
(
t
)
=
∑
n
a
n
g
(
t
−
n
T
s
)
A
c
o
s
2
π
f
c
t
s(t)={\sum_na_ng(t-nT_s)}Acos2\pi f_ct
s(t)=n∑ang(t−nTs)Acos2πfct
其中,
a
n
∈
a_n\in
an∈ {0,1},
g
(
t
)
=
{
1
0
≤
t
≤
T
s
0
其他
g(t)=\begin{cases} 1& 0\le t \le T_s \\ 0& \text{其他} \end{cases}
g(t)={100≤t≤Ts其他
可以看到,上式是数字基带信号
m
(
t
)
=
∑
n
a
n
g
(
t
−
n
T
s
)
m(t)=\sum_na_ng(t-nT_s)
m(t)=∑nang(t−nTs) 经过 DSB 调制后形成的信号,OOK 信号波形如下图所示:
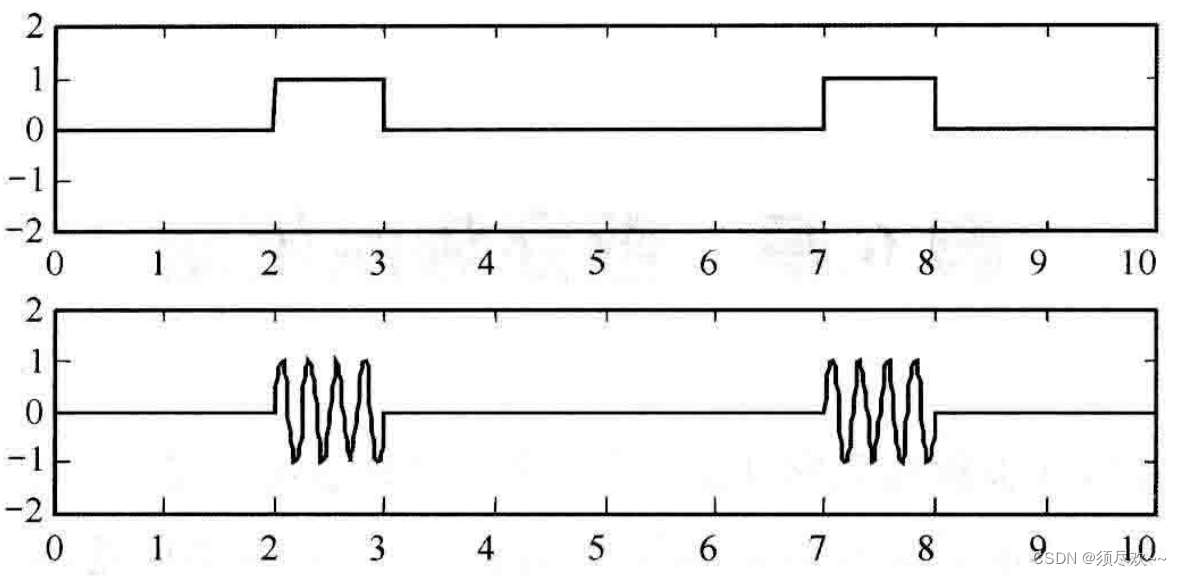
2、功率谱密度
OOK 信号的功率谱密度为:
P
s
(
f
)
=
A
2
4
[
P
m
(
f
−
f
c
)
+
P
m
(
f
+
f
c
)
]
P_s(f)=\frac{A^2}{4}[P_m(f-f_c)+P_m(f+f_c)]
Ps(f)=4A2[Pm(f−fc)+Pm(f+fc)]
3、调制框图
OOK 的调制框图如下图所示:
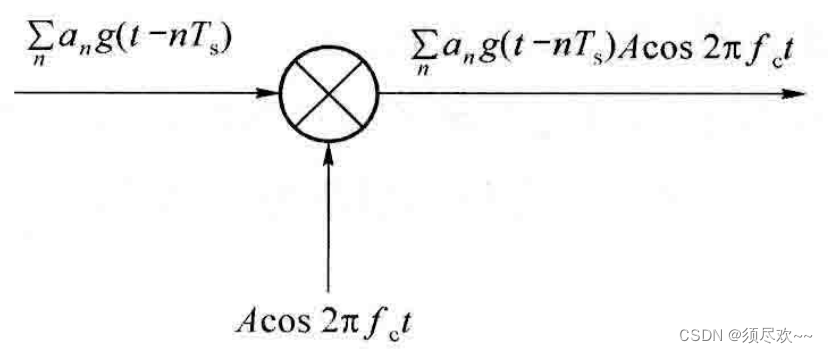
二、2PSK
1、表达式
将二进制码元 “0” 对应相位为
π
\pi
π 的载波
−
A
c
o
s
2
π
f
c
t
-Acos2\pi f_ct
−Acos2πfct,“1” 对应相位为 0 的载波
A
c
o
s
2
π
f
c
t
Acos2 \pi f_ct
Acos2πfct,则 2PSK 信号可以写成如下表达式:
s
(
t
)
=
∑
n
a
n
g
(
t
−
n
T
s
)
A
c
o
s
2
π
f
c
t
s(t)={\sum_na_ng(t-nT_s)}Acos2\pi f_ct
s(t)=n∑ang(t−nTs)Acos2πfct
其中,
a
n
∈
a_n\in
an∈ {+1,-1},
g
(
t
)
=
{
1
0
≤
t
≤
T
s
0
其他
g(t)=\begin{cases} 1& 0\le t \le T_s \\ 0& \text{其他} \end{cases}
g(t)={100≤t≤Ts其他
2PSK 信号波形如下图所示,其实现框图与 OOK 相同,只是输入是双极性的
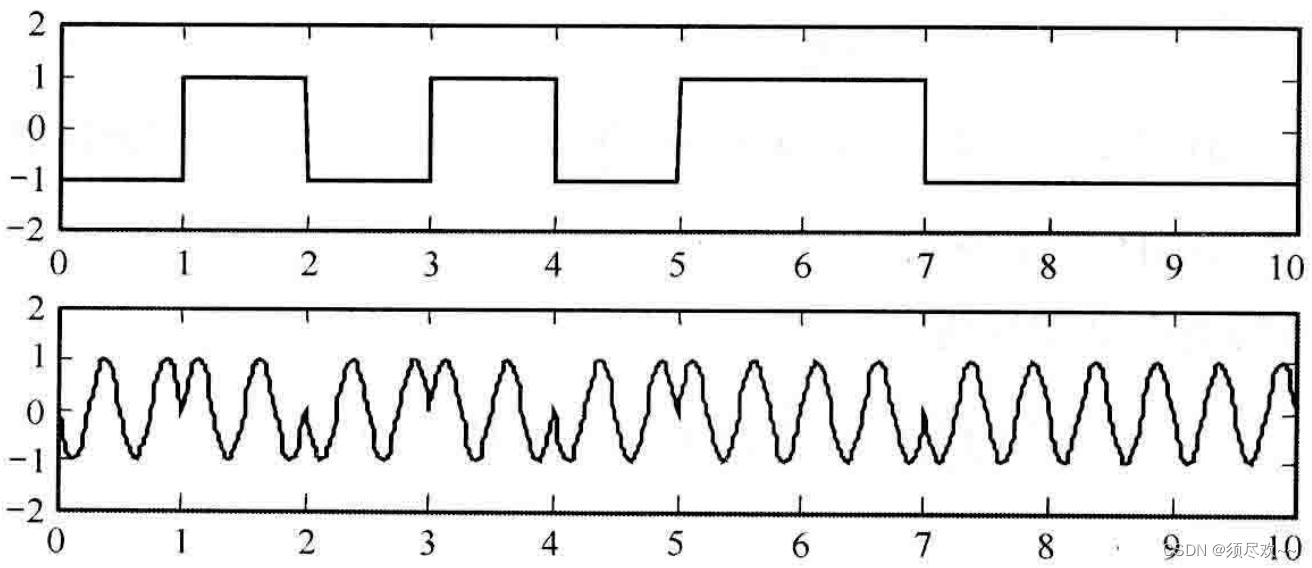
2、功率谱密度
2PSK 信号的功率谱密度为:
P
s
(
f
)
=
A
2
4
[
P
m
(
f
−
f
c
)
+
P
m
(
f
+
f
c
)
]
P_s(f)=\frac{A^2}{4}[P_m(f-f_c)+P_m(f+f_c)]
Ps(f)=4A2[Pm(f−fc)+Pm(f+fc)]
三、2FSK
1、表达式
将二进制码元 “0” 对应载波
A
c
o
s
2
π
f
1
t
Acos2 \pi f_1t
Acos2πf1t,“1” 对应载波
A
c
o
s
2
π
f
2
t
Acos2\pi f_2t
Acos2πf2t,则形成 2FSK 信号,可以写成如下表达式:
s
(
t
)
=
∑
n
a
n
‾
g
(
t
−
n
T
s
)
A
c
o
s
(
2
π
f
1
t
+
φ
n
)
+
∑
n
a
n
g
(
t
−
n
T
s
)
A
c
o
s
(
2
π
f
1
t
+
θ
n
)
s(t)=\sum_n \overline{a_n}g(t-nT_s)Acos(2\pi f_1t+\varphi_n)+\sum_n a_ng(t-nT_s)Acos(2\pi f_1t+\theta_n)
s(t)=n∑ang(t−nTs)Acos(2πf1t+φn)+n∑ang(t−nTs)Acos(2πf1t+θn)
当
a
n
=
1
a_n=1
an=1 时,对应的传输信号频率为
f
2
f_2
f2,当
a
n
=
0
a_n=0
an=0 时,对应的传输信号频率为
f
1
f_1
f1,上式中,
φ
n
\varphi_n
φn、
θ
n
\theta_n
θn 时两个频率波的初相。2FSK 也可以写成另外的形式如下:
s
(
t
)
=
A
c
o
s
[
2
π
f
c
t
+
2
π
h
∑
n
=
−
∞
∞
a
n
g
(
t
−
n
T
s
)
]
s(t)=Acos[2\pi f_ct+2\pi h\sum_{n=-\infty}^{\infty}{a_n}g(t-nT_s)]
s(t)=Acos[2πfct+2πhn=−∞∑∞ang(t−nTs)]
其中,
a
n
∈
a_n\in
an∈ {+1,-1},
f
c
=
(
f
1
+
f
2
)
/
2
f_c=(f_1+f_2)/2
fc=(f1+f2)/2,
g
(
t
)
=
{
1
0
≤
t
≤
T
s
0
其他
g(t)=\begin{cases} 1& 0\le t \le T_s \\ 0& \text{其他} \end{cases}
g(t)={100≤t≤Ts其他,
h
=
∣
f
c
−
f
1
∣
h=|f_c-f_1|
h=∣fc−f1∣ 为频偏,其波形如下图所示:
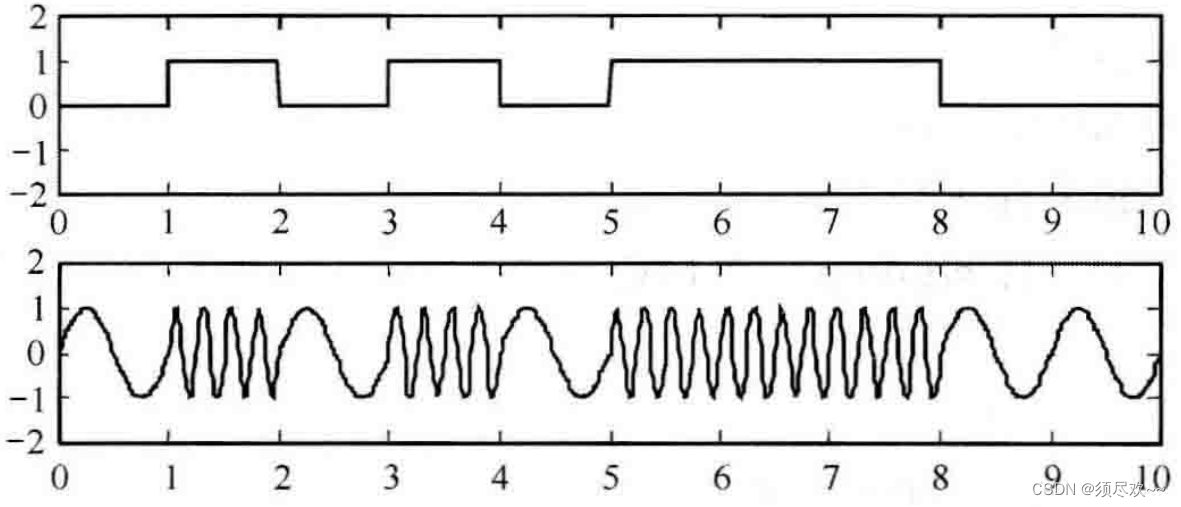
2FSK 信号可以看成是两个不同载波的 OOK 信号的叠加:
s
(
t
)
=
s
1
(
t
)
c
o
s
(
ω
t
+
ϕ
1
)
+
s
2
(
t
)
c
o
s
(
ω
t
+
ϕ
2
)
s(t)=s_1(t)cos(\omega t+\phi_1)+s_2(t)cos(\omega_t+\phi_2)
s(t)=s1(t)cos(ωt+ϕ1)+s2(t)cos(ωt+ϕ2)
当这两项不相关时(如载波之间频率差足够大),它的功率谱密度为:
P
s
=
1
4
[
P
s
1
(
f
+
f
1
)
+
P
s
1
(
f
−
f
1
)
]
+
1
4
[
P
s
2
(
f
+
f
1
)
+
P
s
1
(
f
−
f
2
)
]
P_s=\frac{1}{4}[P_{s1}(f+f_1)+P_{s1}(f-f_1)]+\frac{1}{4}[P_{s2}(f+f_1)+P_{s1}(f-f_2)]
Ps=41[Ps1(f+f1)+Ps1(f−f1)]+41[Ps2(f+f1)+Ps1(f−f2)]
四、MATLAB 仿真
以下代码使用 MATLAB 产生独立等概的二进制信源,并完成了下面三个功能:
- 画出 OOK 信号波形及其功率谱;
- 画出 2PSK 信号波形及其功率谱;
- 画出 2FSK 信号波形及其功率谱(设 ∣ f 1 − f 2 ∣ > > 1 T s |f_1-f_2|>>\frac{1}{T_s} ∣f1−f2∣>>Ts1)。
1、MATLAB 源码
% 2ASK,2PSK
clear all;
close all;
A = 1;
fc = 2; % 2Hz;
N_sample = 8;
N = 500; % 码元数
Ts = 1; % 1 baud/s
dt = Ts/fc/N_sample; % 波形采样间隔
t = 0 : dt : N*Ts-dt;
T = dt * length(t);
Lt = length(t);
% 产生二进制信源
d = sign(randn(1, N));
dd = sigexpand((d+1)/2, fc*N_sample);
gt = ones(1, fc*N_sample); % NRZ 波形
figure(1)
subplot(221); % 输入 NRZ 信号波形(单极性)
d_NRZ = conv(dd, gt);
plot(t, d_NRZ(1:length(t)));
axis([0 10 0 1.2]); xlabel('t/s'); ylabel('输入信号');
subplot(222); % 输入 NRZ 频谱
[f, d_NRZf] = T2F(t, d_NRZ(1:length(t)));
plot(f, 10*log10(abs(d_NRZf).^2/T));
axis([-2 2 -50 10]); xlabel('f/Hz'); ylabel('输入信号功率谱密度(dB/Hz)');
%2ASK信号
ht = A*cos(2*pi*fc*t);
s_2ask = d_NRZ(1:Lt).*ht;
subplot(223)
plot(t,s_2ask);
axis([0 10 -1.2 1.2]); xlabel('t/s'); ylabel('2ASK');
[f, s_2askf]=T2F(t, s_2ask );
subplot(224)
plot(f, 10*log10(abs(s_2askf).^2/T));
axis([-fc-4 fc+4 -50 10]); xlabel('f/Hz'); ylabel('2ASK功率谱密度(dB/Hz)');
figure(2)
%2PSK信号
d_2psk = 2*d_NRZ-1;
s_2psk = d_2psk(1:Lt).*ht;
subplot(221)
plot(t,s_2psk);
axis([0 10 -1.2 1.2]); xlabel('t/s'); ylabel('2PSK');
subplot(222)
[f, s_2pskf] = T2F(t, s_2psk);
plot( f, 10*log10(abs(s_2pskf).^2/T) );
axis([-fc-4 fc+4 -50 10]); xlabel('f/Hz'); ylabel('2PSK功率谱密度(dB/Hz)');
% 2FSK
% s_2fsk = Acos(2*pi*fc*t + int(2*d_NRZ-1) );
sd_2fsk = 2*d_NRZ-1;
s_2fsk = A*cos(2*pi*fc*t + 2*pi*sd_2fsk(1:length(t)).*t );
subplot(223)
plot(t, s_2fsk);
axis([0 10 -1.2 1.2]);xlabel('t/s'); ylabel('2FSK')
subplot(224)
[f, s_2fskf] = T2F(t, s_2fsk);
plot(f, 10*log10(abs(s_2fskf).^2/T));
axis([-fc-4 fc+4 -50 10]); xlabel('f/Hz'); ylabel('2FSK功率谱密度(dB/Hz)');
% 随机相位 2FSK
fai = 2*pi*rand(1, N);
fai_2fsk = sigexpand(fai, fc*N_sample);
fai_2fsk = conv(fai_2fsk, gt);
s_2fskd = A*cos(2*pi*fc*t + 2*pi*sd_2fsk(1:length(t)).*t + fai_2fsk(1:length(t)) );
figure(3)
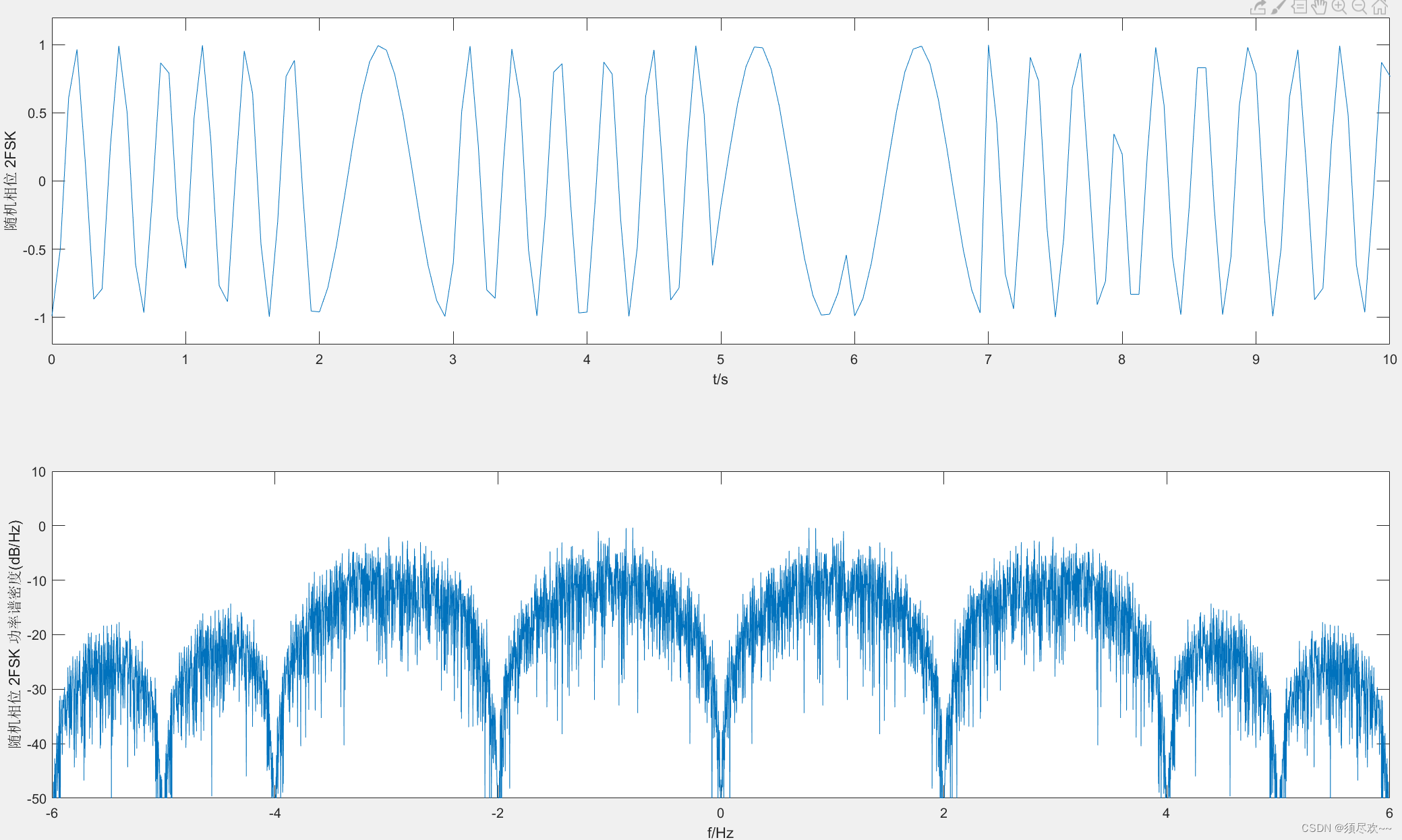
subplot(211);
plot(t, s_2fskd);
axis([0 10 -1.2 1.2]); xlabel('t/s'); ylabel('随机相位 2FSK');
[f, s_2fskdf] = T2F(t, s_2fskd);
subplot(212);
plot(f, 10*log10(abs(s_2fskdf).^2/T));
axis([-fc-4 fc+4 -50 10]); xlabel('f/Hz'); ylabel('随机相位 2FSK 功率谱密度(dB/Hz)');
2、仿真及结果
①、输入信号及频谱图
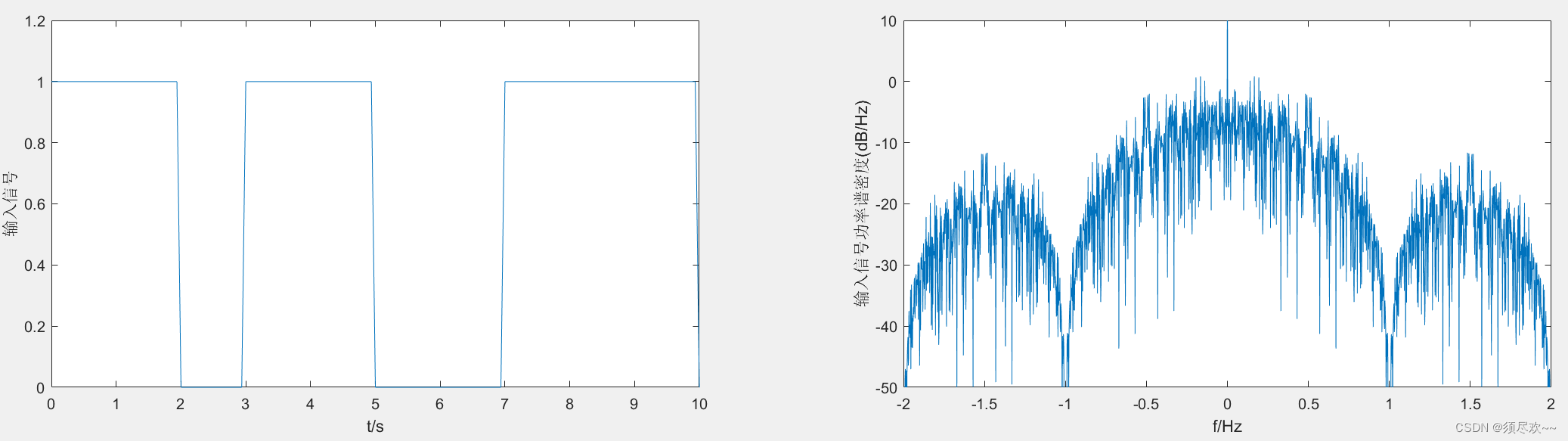
②、2ASK 调制
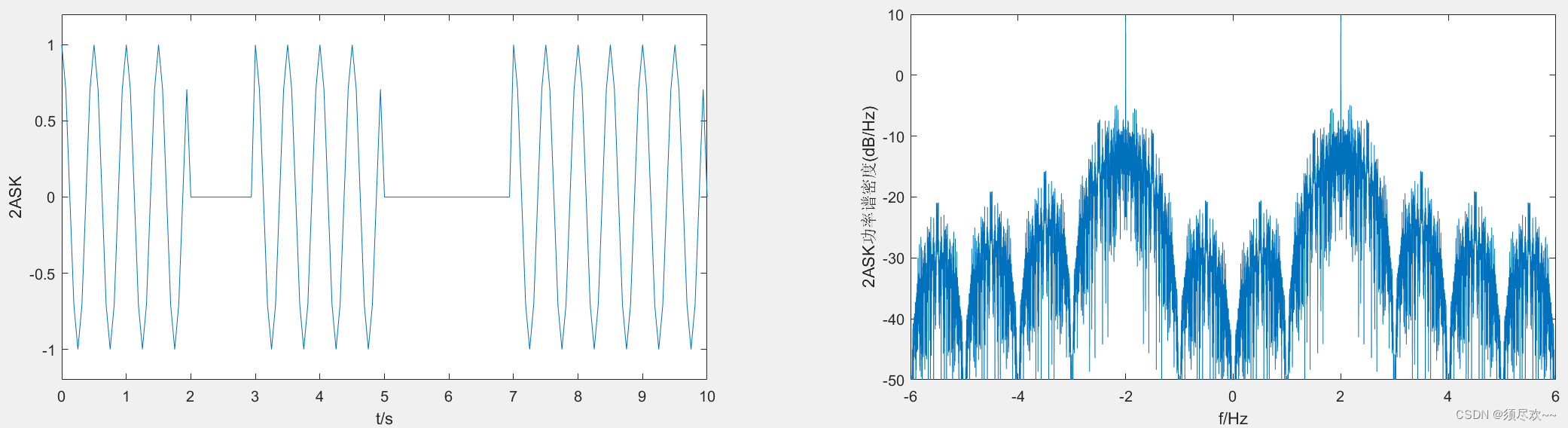
③、2PSK 调制
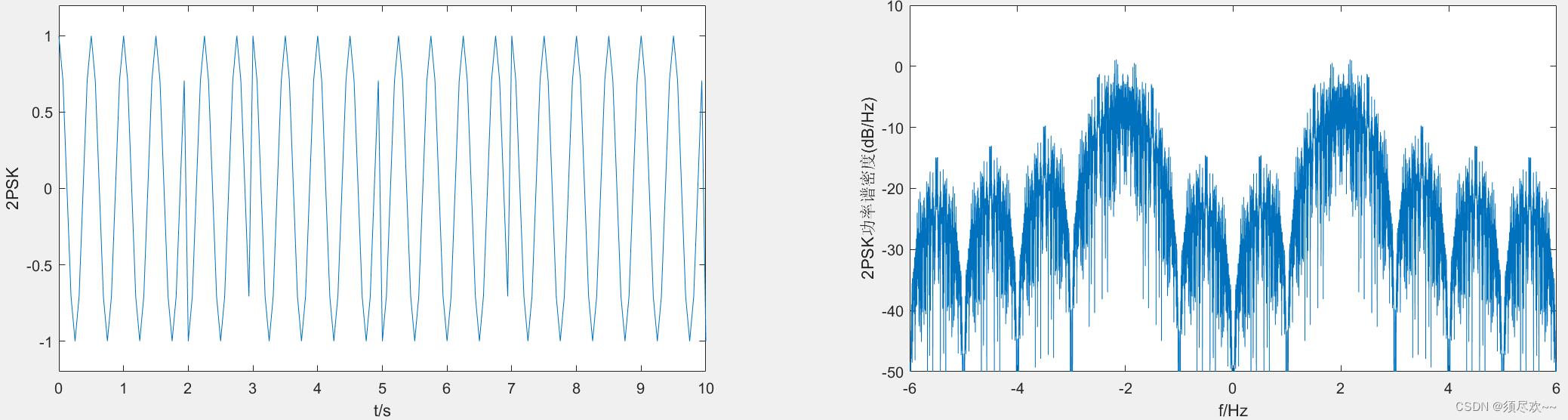
④、2FSK 调制
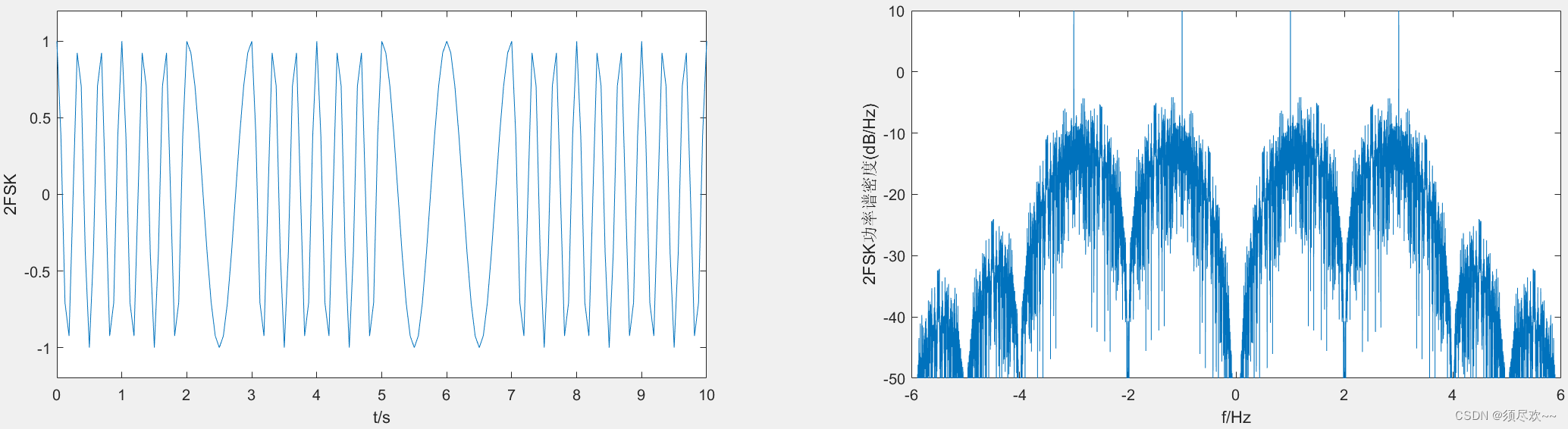
⑤、随机相位 2FSK 调制
五、资源自取
二进制数字调制及MATLAB仿真
我的qq:2442391036,欢迎交流!