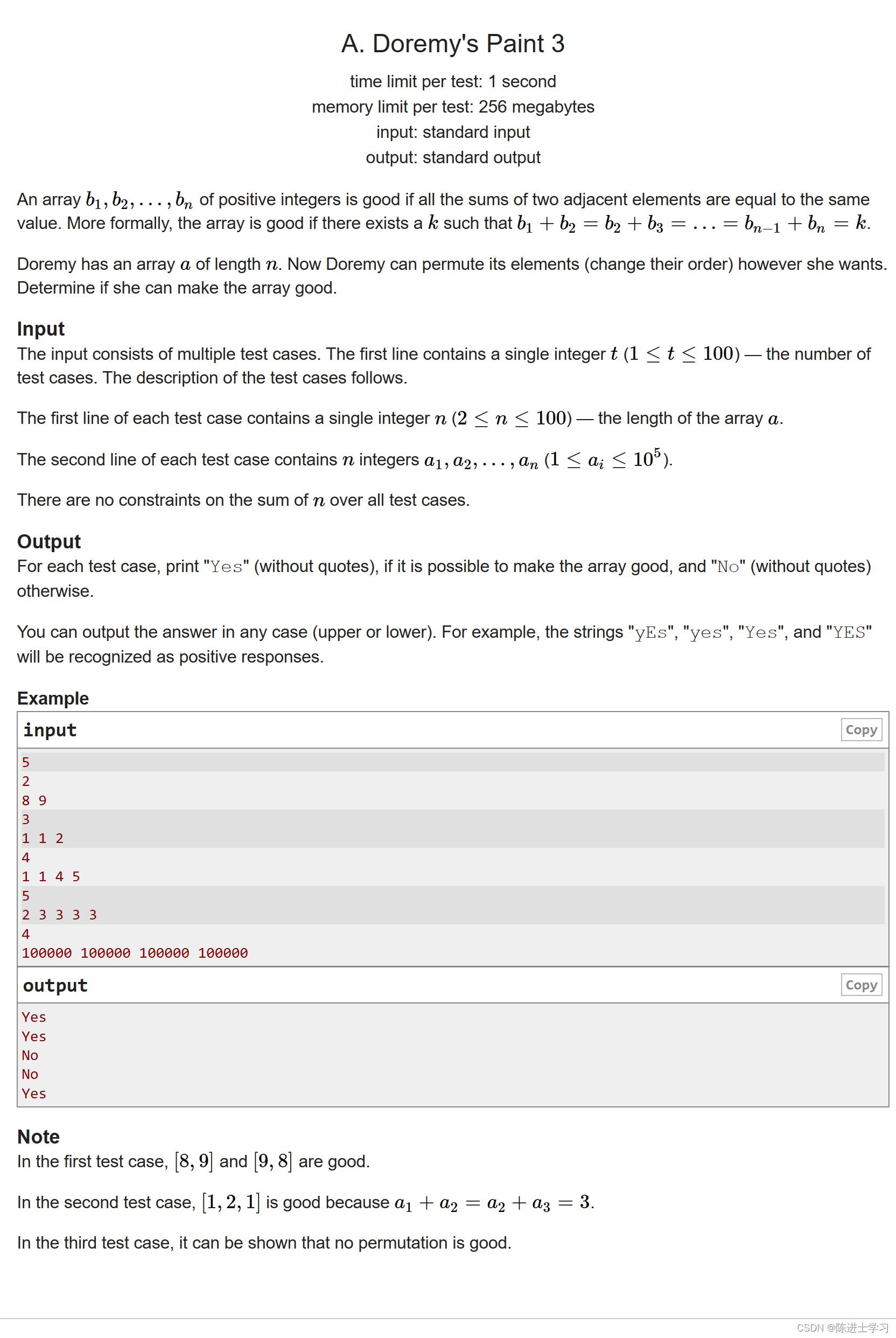
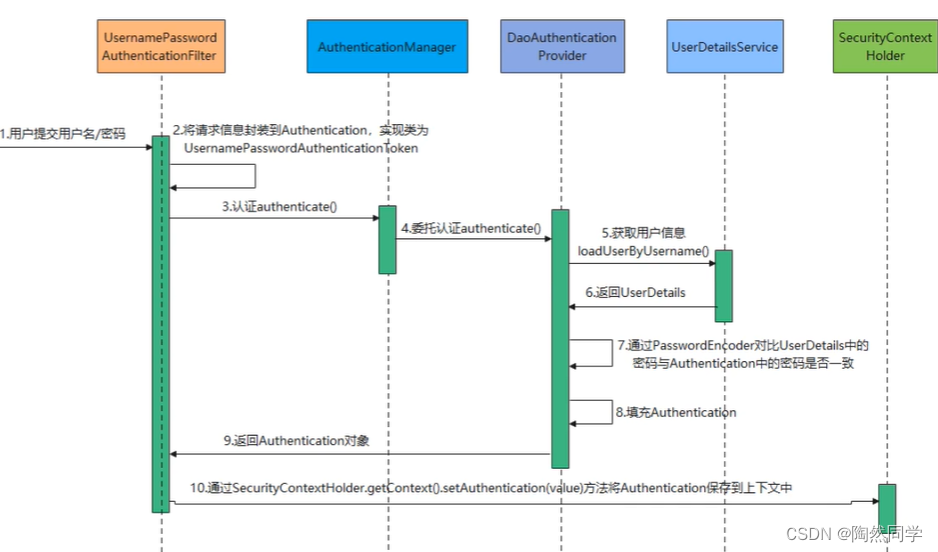
原始 Markdown文档、Visio流程图、XMind思维导图见:https://github.com/LiZhengXiao99/Navigation-Learning

文章目录
- 一、SPP 解算
- 1、spp():单点定位主入口函数
- 2、estpos()
- 3、estpose_()
- 4、valsol():GDOP和卡方检验结果有效性
- 二、卫星位置钟差计算
- 1、satposs_rtklib()
- 2、ephclk()
- 3、ephpos()
- 1. eph2pos():
- 2. var_uraeph():用URA用户测距精度标定卫星位置方差
- 3. geph2pos():由 GLONASS 星历计算卫星位置钟差
- 4. glorbit():龙格库塔迭代
- 5. deq():微分方程计算
- 4、peph2pos():精密星历计算卫星位置、钟差、速度、钟漂
- 1. 精密星历读取流程
- 2. pephpos():精密星历计算卫星位置,钟差
- 3. interppol():Neville 插值
- 4. posWithEarhRotation():
- 5. pephclk():精密钟差计算卫星钟差
- 三、rescode():残差计算、设计矩阵构建
- 1、geodist():计算近似几何距离、接收机到卫星方向的观测矢量,sagnac 效应改正
- 2、satazel():计算方位角高度角
- 3、prange():差分码偏差改正
- 4、gettgd():
- 4、satexclude():排除不可用卫星的观测值
- 5、ionocorr():根据选项模型计算 L1 电离层延迟 I
- 6、ionmodel():克罗布歇模型电离层延迟计算
- 7、tropcorr():对流层改正
- 8、tropmodel():Saastamoinen 模型计算对流层延迟
- 7、varerr():计算伪距量测协方差
- 8、getHVR_spp
- 四、lsqplus():最小二乘估计
一、SPP 解算
1、spp():单点定位主入口函数
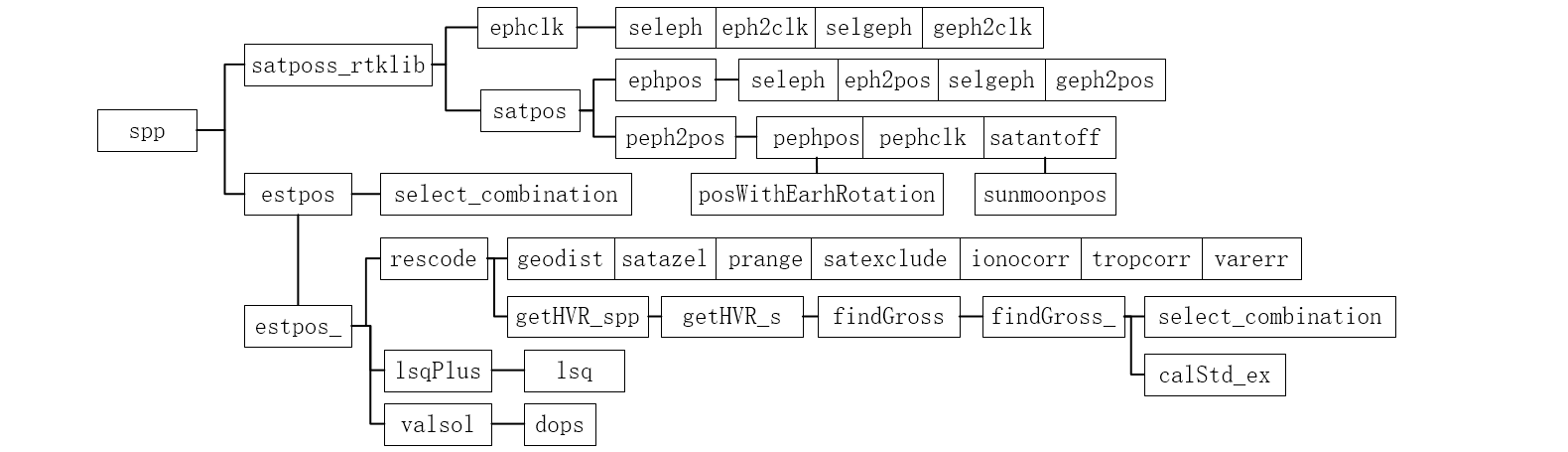
默认使用广播星历计算卫星位置、钟差,使用克罗布歇模型通过广播星历中的参数计算电离层延迟,使用 Saastamoinen 模型计算对流层延迟。
-
调用
satposs_rtklib()计算卫星位置、卫星钟差:rs[(0:2)+i*6]:卫星位置 {x,y,z} (m)rs [(3:5)+i*6]:卫星速度 {vx,vy,vz} (m/s)dts[(0:1)+i*2]:卫星钟差 {bias,drift} (s|s/s)var[i]:卫星位置和钟差的协方差 (m^2)svh[i]:卫星健康标志 (-1:correction not available)
-
调用
estpos()计算接收机位置:加权最小二乘,其中会调用 valsol 进行卡方检验和GDOP检验。 -
存入方位角和俯仰角 ,赋值解算状态结构体 ssat。
2、estpos()
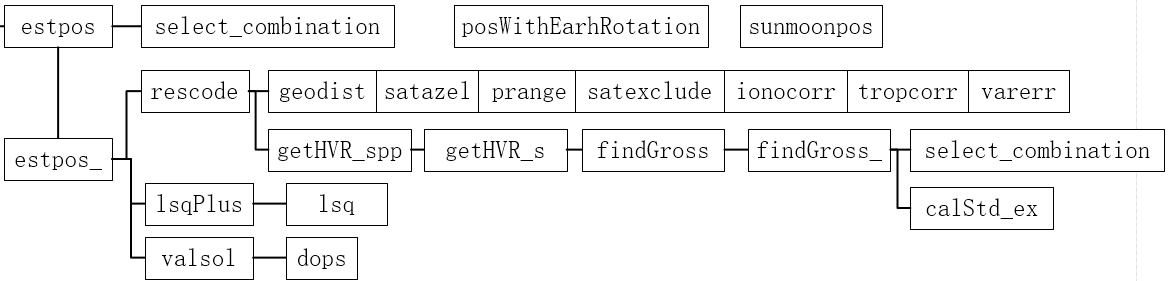
3、estpose_()

先给矩阵开辟内存空间,待估参数 dx 赋值为 0,然后进入最小二乘迭代求解:
-
先调用
rescode()计算当前迭代的伪距残差 v、设计矩阵 H、伪距残差的方差 var、所有观测卫星的方位角和仰角 azel,定位时有效性 vsat、定位后伪距残差 resp、参与定位的卫星个数ns和方程个数nv。 -
然后对 H、V 协方差加权,以 varerr() 计算出的伪距残差的标准差的倒数作为权重,对
H和v分别左乘权重对角阵,得到加权之后的H和v。
W = diag ( σ 1 − 2 , σ 2 − 2 , … , σ m − 2 ) σ 2 = F s R r ( a σ 2 + b σ 2 / sin E l r s ) + σ eph 2 + σ ion 2 + σ trop 2 + σ bias 2 \begin{array}{l}\boldsymbol{W}=\operatorname{diag}\left(\sigma_{1}^{-2}, \sigma_{2}^{-2}, \ldots, \sigma_{m}^{-2}\right) \\ \sigma^{2}=F^{s} R_{r}\left(a_{\sigma}{ }^{2}+b_{\sigma}{ }^{2} / \sin E l_{r}^{s}\right)+{\sigma_{\text {eph }}}^{2}+{\sigma_{\text {ion }}}^{2}+{\sigma_{\text {trop }}}^{2}+{\sigma_{\text {bias }}}^{2}\end{array} W=diag(σ1−2,σ2−2,…,σm−2)σ2=FsRr(aσ2+bσ2/sinElrs)+σeph 2+σion 2+σtrop 2+σbias 2 -
调用
lsqPlus()最小二乘解算,计算状态x的增量dx -
最后状态反馈,把
dx置加到x上
结束迭代有两种情况:
-
最小二乘求解后,dx 的模 d0 小于 1E-4 ,存结果到 sol,调用
valsol()卡方和 GDOP 检验结果有效,结果状态设为单点解。 -
超出迭代次数上限(10次),不存结果,输出迭代发散的消息。
static int estpos_(int *bDeleted, double *x,const obsd_t *obs, int n, const double *rs, const double *dts, const double *vare,
const int *svh, const nav_t *nav, const prcopt_t *opt, sol_t *sol, double *azel, int *vsat, double *resp, char *msg)
{
int i,j,k,info,stat=0,nx,nv,bElevCVG;
double dx[NX_SPP],Q[NX_SPP*NX_SPP],dop[4],*v,*H,*var,sig,d0;
bElevCVG=0;
v=mat(n+5,1); H=mat(NX_SPP,n+5); var=mat(n+5,1);
for (i=0;i<NX_SPP;i++) dx[i]=0.0;
for (i=0;i<MAXITR;i++) {
// 调用 rescode() 计算设计矩阵 H、残差 V
/* pseudorange residuals */
nv=rescode(i,bElevCVG,obs,n,rs,dts,vare,svh,nav,x,opt,v,H,var,azel,vsat,resp,&nx,bDeleted);
if (nv<nx) {
sprintf(msg,"lack of valid sats ns=%d",nv);
break;
}
// H、V 协方差加权
/* weight by variance */
for (j=0;j<nv;j++) {
sig=sqrt(var[j]);
v[j]/=sig;
for (k=0;k<NX_SPP;k++) H[k+j*NX_SPP]/=sig;
}
// 调用 lsqPlus() 最小二乘解算
/* least square estimation */
if ((info=lsqPlus(H,v,NX_SPP,nv,dx,Q))) {
sprintf(msg,"lsq error info=%d",info);
sprintf(PPP_Glo.chMsg, "%s\n",msg);
outDebug(OUTWIN,OUTFIL,OUTTIM);
break;
}
// 状态反馈
for (j=0;j<NX_SPP;j++) x[j]+=dx[j];
d0=norm(dx,NX_SPP);
if (d0<1E4) bElevCVG=1;
else bElevCVG=0;
if (d0<1E-4) {
sol->type=0;
sol->time=timeadd(obs[0].time,-x[3]/CLIGHT); // 加上钟差
sol->dtr[0]=x[3]/CLIGHT; /* receiver clock bias (s) */
sol->dtr[1]=x[4]/CLIGHT; /* glo-gps time offset (s) */
sol->dtr[2]=x[5]/CLIGHT; /* bds-gps time offset (s) */
sol->dtr[3]=x[6]/CLIGHT; /* gal-gps time offset (s) */
sol->dtr[4]=x[7]/CLIGHT; /* qzs-gps time offset (s) */
for (j=0;j<6;j++) sol->rr[j]=j<3?x[j]:0.0;
for (j=0;j<3;j++) sol->qr[j]=(float)Q[j+j*NX_SPP];
sol->qr[3]=(float)Q[1]; /* cov xy */
sol->qr[4]=(float)Q[2+NX_SPP]; /* cov yz */
sol->qr[5]=(float)Q[2]; /* cov zx */
sol->ns[0]=(unsigned char)nv;
sol->rms=sol->dop[0]=sol->dop[1]=sol->dop[2]=sol->dop[3]=0.0;
// 调用 valsol() 卡方和 GDOP 检验结果有效性
/* validate solution */
if ((stat=valsol(azel,vsat,n,opt,v,nv,nx,msg,dop)))
sol->stat=SOLQ_SINGLE;
sol->dop[0]=dop[0];
sol->dop[1]=dop[1];
sol->dop[2]=dop[2];
sol->dop[3]=dop[3];
break;
}
}
if (i>=MAXITR) sprintf(msg,"iteration divergent i=%d",i);
free(v); free(H); free(var);
return stat;
}
4、valsol():GDOP和卡方检验结果有效性
低成本接收机可能通不过检验,可禁用此函数
const double *azel 方位角、高度角
const int *vsat 观测卫星在当前定位时是否有效 (1*n)
int n 观测值个数
const prcopt_t *opt 处理选项
const double *v 定位方程的右端部分,伪距残差
int nv 观测值数
int nx 待估计参数数
char *msg 错误消息
v s = ( P r s − ( ρ ^ r s + c d ^ t r − c d T s + I r s + T r s ) ) σ s v = ( v 1 , v 2 , v 3 , … , v m ) T v T v m − n − 1 < χ α 2 ( m − n − 1 ) G D O P < G D O P thres \begin{array}{l}v_{s}=\frac{\left(P_{r}^{s}-\left(\hat{\rho}_{r}^{s}+c \hat{d} t_{r}-c d T^{s}+I_{r}^{s}+T_{r}^{s}\right)\right)}{\sigma_{s}} \\ \boldsymbol{v}=\left(v_{1}, v_{2}, v_{3}, \ldots, v_{m}\right)^{T} \\ \frac{\boldsymbol{v}^{T} \boldsymbol{v}}{m-n-1}<\chi_{\alpha}^{2}(m-n-1) \\ G D O P<G D O P_{\text {thres }}\end{array} vs=σs(Prs−(ρ^rs+cd^tr−cdTs+Irs+Trs))v=(v1,v2,v3,…,vm)Tm−n−1vTv<χα2(m−n−1)GDOP<GDOPthres
二、卫星位置钟差计算
1、satposs_rtklib()
gtime_t teph I (gpst) 用于选择星历的时刻 (gpst)
obsd_t *obs I OBS观测数据
int n I OBS数
nav_t *nav I NAV导航电文
int ephopt I 星历选项 (EPHOPT_???)
double *rs O 卫星位置和速度,长度为6*n,{x,y,z,vx,vy,vz}(ecef)(m,m/s)
double *dts O 卫星钟差,长度为2*n, {bias,drift} (s|s/s)
double *var O 卫星位置和钟差的协方差 (m^2)
int *svh O 卫星健康标志 (-1:correction not available)

-
遍历观测数据,找伪距观测值,除以光速得到信号传播时间,用数据接收时刻减去伪距信号传播时间得到信号发射时刻。
-
调用
ephclk()函数,由广播星历计算出当前观测卫星与 GPS 时间的钟差dt,此时的钟差是没有考虑相对论效应和 TGD 的 ,dt仅作为satpos()的参数,不作为最终计算的钟差。信号发射时刻减去钟差dt,得到 GPS 时间下的卫星信号发射时刻。 -
调用
satpos()对此观测值进行下一步卫星位置钟差的计算;satpos()函数对星历计算选项进行判断,广播星历模式调用ephpos(),精密星历模式调用peph2pos()。最后检测钟差值,如果没有精密星历,则调用ephclk()用广播星历计算钟差。
extern void satposs_rtklib(gtime_t teph, const obsd_t *obs, int n, const nav_t *nav,
int ephopt, double *rs, double *dts, double *var, int *svh)
{
gtime_t time[MAXOBS]={{0}};
double dt,pr;
int i,j;
for (i=0;i<n&&i<2*MAXOBS;i++) {
for (j=0;j<6;j++) rs [j+i*6]=0.0;
for (j=0;j<2;j++) dts[j+i*2]=0.0;
var[i]=0.0; svh[i]=0;
/* search any psuedorange */
for (j=0,pr=0.0;j<NFREQ;j++) if ((pr=obs[i].P[j])!=0.0) break;
if (j>=NFREQ) {
sprintf(PPP_Glo.chMsg,"*** WARNING: no pseudorange %s sat=%2d\n",
time_str(obs[i].time,3),obs[i].sat);
outDebug(OUTWIN,OUTFIL,0);
continue;
}
/* transmission time by satellite clock */
time[i]=timeadd(obs[i].time,-pr/CLIGHT);
/* satellite clock bias by broadcast ephemeris */
if (!ephclk(time[i],teph,obs[i].sat,nav,&dt)) {
sprintf(PPP_Glo.chMsg,"*** WARNING: no broadcast clock %s sat=%2d\n",
time_str(time[i],3),obs[i].sat);
outDebug(0,OUTFIL,0);
continue;
}
time[i]=timeadd(time[i],-dt);
/* satellite position and clock at transmission time */
if (!satpos(time[i],teph,obs[i].sat,ephopt,nav,rs+i*6,dts+i*2,var+i,
svh+i)) {
sprintf(PPP_Glo.chMsg,"*** WARNING: no ephemeris %s sat=%2d\n",
time_str(time[i],3),obs[i].sat);
outDebug(0,0,0);
continue;
}
/* if no precise clock available, use broadcast clock instead */
if (dts[i*2]==0.0) {
if (!ephclk(time[i],teph,obs[i].sat,nav,dts+i*2)) continue;
dts[1+i*2]=0.0;
*var=SQR(STD_BRDCCLK);
}
}
}
2、ephclk()
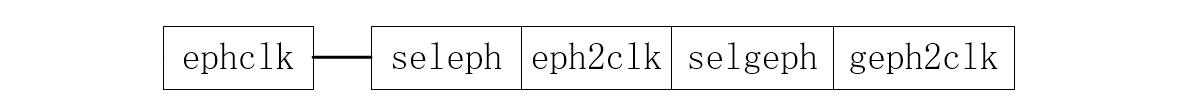
-
单观测值卫星钟差计算。由于 GLONASS 系统的计算和其它的区别较大,先进行判断。
-
如果不是 GLONASS 则调用
seleph()选择与观测值对应的星历,调用eph2clk()根据广播星历参数 a 0 a_0 a0、 a 1 a_1 a1、 a 2 a_2 a2 计算卫星钟差(迭代 3 次); -
如果是 GLONASS 则调用
selgeph()选择与观测值对应的星历,调用geph2clk()根据广播星历参数 t a u n t_aun taun、 g a u n g_aun gaun 计算卫星钟差(迭代 3 次)。
static int ephclk(gtime_t time, gtime_t teph, int sat, const nav_t *nav,
double *dts)
{
eph_t *eph;
geph_t *geph;
int sys;
sys=satsys(sat,NULL);
if (sys==SYS_GPS||sys==SYS_GAL||sys==SYS_QZS||sys==SYS_CMP) {
if (!(eph=seleph(teph,sat,-1,nav))) return 0;
*dts=eph2clk(time,eph);
}
else if (sys==SYS_GLO) {
if (!(geph=selgeph(teph,sat,-1,nav))) return 0;
*dts=geph2clk(time,geph);
}
else return 0;
return 1;
}
1. eph2clk():时钟校正参数( a f 0 、 a f 1 、 a f 2 a_{f0}、a_{f1}、a_{f2} af0、af1、af2)计算卫星钟差
相对于 GPS 时间,卫星上作为时间和频率信号来源的原子钟也存在时间偏差和频率漂移。为确保各颗卫星的时钟与GPS时间同步,GPS地面监控部分通过对卫星信号进行检测,将卫星时钟在GPS时间t的卫星钟差
Δ
t
(
s
)
\Delta t^{(s)}
Δt(s) 描述为如下二项式:
Δ
t
(
s
)
=
a
f
0
+
a
f
1
(
t
−
t
o
c
)
+
a
f
2
(
t
−
t
o
c
)
2
\Delta t^{(s)}=a_{f0}+a_{f1}(t-t_{oc})+a_{f2}(t-t_{oc})^2
Δt(s)=af0+af1(t−toc)+af2(t−toc)2
extern double eph2clk(gtime_t time, const eph_t *eph)
{
double t;
int i;
t=timediff(time,eph->toc); // 计算与星历参考时间的偏差 dt = t-toc
// 利用二项式校正计算出卫星钟差,从 dt中减去这部分,然后再进行一次上述操作,得到最终的 dt
for (i=0;i<2;i++) {
t-=eph->f0+eph->f1*t+eph->f2*t*t;
}
// 使用二项式校正得到最终的钟差
return eph->f0+eph->f1*t+eph->f2*t*t;
}
除此以外,卫星钟差一般还需考虑相对论效应校正、群波延迟校正、钟漂校正:
相对论效应校正 Δ t r \Delta t_r Δtr
综合狭义相对论和广义相对论,在高空中高速运行的卫星原子钟比地面上一模一样的原子钟每天要快 38000ns ,每秒快 0.44ns 。如果不考虑相对论效应,GPS 发上天两分钟内,卫星原子钟就会失去定位作用。在地面上设计原子钟时可以减小一点点它的频率,上天以后其时钟频率在地面上看来正好等于设计值。同时因为GPS运行轨道是椭圆而不是圆,地面上计算机还有根据卫星当前位置做相对论效应的校如下:
Δ
t
r
=
F
e
s
a
s
sin
E
k
\Delta t_r=Fe_s\sqrt{a_s} \sin E_k
Δtr=FesassinEk
群波延迟校正 T G D T_{GD} TGD
由第一数据块给出,只适用于单频。这样对于 L1 单频接收机,卫星时钟总钟差值如下:
δ
t
(
s
)
=
Δ
t
(
s
)
+
Δ
t
r
−
T
G
D
\delta t^{(s)}=\Delta t^{(s)}+\Delta t_{r}-T_{G D}
δt(s)=Δt(s)+Δtr−TGD
钟漂校正
对上面卫星时钟总钟差值求导得:
δ
f
(
s
)
=
a
f
1
+
2
a
f
2
(
t
−
t
o
c
)
+
Δ
t
˙
r
\delta f^{(s)}=a_{f 1}+2 a_{f 2}\left(t-t_{o c}\right)+\Delta \dot{t}_r
δf(s)=af1+2af2(t−toc)+Δt˙r
群波延迟校正
T
G
D
T_{GD}
TGD 的导数为 0,相对论效应校正
Δ
t
r
\Delta t_r
Δtr 如下:
Δ
t
˙
r
=
F
e
s
a
s
E
˙
k
cos
E
k
\Delta \dot{t}_r=F e_s \sqrt{a_s} \dot{E}_k \cos E_k
Δt˙r=FesasE˙kcosEk
2. geph2clk():时钟校正参数( τ n 、 γ n \tau_{n}、\gamma_{n} τn、γn)计算 GLONASS 卫星钟差
d T s ( t ) = − τ n + γ n ( t − t b ) d T^{s}(t)=-\tau_{n}+\gamma_{n}\left(t-t_{b}\right) dTs(t)=−τn+γn(t−tb)
extern double geph2clk(gtime_t time, const geph_t *geph)
{
double t;
int i;
t=timediff(time,geph->toe);
for (i=0;i<2;i++) {
t-=-geph->taun+geph->gamn*t;
}
return -geph->taun+geph->gamn*t;
}
用( τ n 、 γ n \tau_{n}、\gamma_{n} τn、γn)计算 GLONASS 卫星钟差的时候已经考虑了相对论效应了,无需再改正。
3、ephpos()
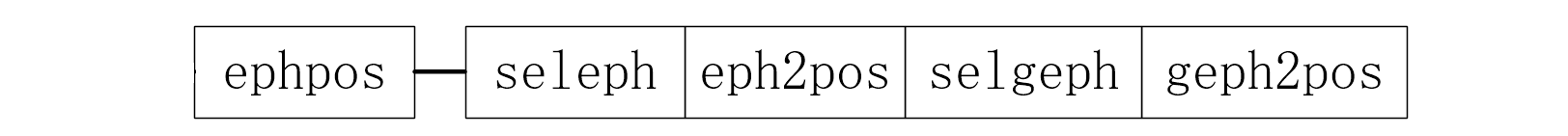
-
与
ephclk()同理,由于 GLONASS 系统的计算和其它的区别较大,先进行判断。 -
如果不是 GLONASS 则调用
seleph()选择与观测值对应的星历,调用eph2pos()根据广播星历中的开普勒轨道参数和摄动改正计算卫星位置(对北斗 MEO、IGSO 卫星会进行特殊处理)、校正卫星钟差的相对论效应、调用var_uraeph()用 URA 值来标定方差。 -
如果是 GLONASS 则调用
selgeph()选择与观测值对应的星历,调用geph2pos()根据广播星历中 PZ-90 坐标系下卫星状态向量四阶龙格库塔迭代计算卫星位置。 -
计算完一次位置之后,加上一个极小的时间,再计算一次位置,两次计算出的时间作差求得卫星速度钟漂。
static int ephpos(gtime_t time, gtime_t teph, int sat, const nav_t *nav,
int iode, double *rs, double *dts, double *var, int *svh)
{
eph_t *eph;
geph_t *geph;
seph_t *seph;
double rst[3],dtst[1],tt=1E-3;
int i,sys;
trace(4,"ephpos : time=%s sat=%2d iode=%d\n",time_str(time,3),sat,iode);
sys=satsys(sat,NULL); //调用 satsys 函数,确定该卫星所属的导航系统。
*svh=-1;
if (sys==SYS_GPS||sys==SYS_GAL||sys==SYS_QZS||sys==SYS_CMP||sys==SYS_IRN) {
if (!(eph=seleph(teph,sat,iode,nav))) return 0; //调用 seleph 函数来选择广播星历。
eph2pos(time,eph,rs,dts,var); //根据选中的广播星历,调用 eph2pos 函数来计算信号发射时刻卫星的 位置、钟差和相应结果的误差。
time=timeadd(time,tt);
eph2pos(time,eph,rst,dtst,var);
*svh=eph->svh;
}
else if (sys==SYS_GLO) {
if (!(geph=selgeph(teph,sat,iode,nav))) return 0;
geph2pos(time,geph,rs,dts,var);
time=timeadd(time,tt);
geph2pos(time,geph,rst,dtst,var);
*svh=geph->svh;
}
else if (sys==SYS_SBS) {
if (!(seph=selseph(teph,sat,nav))) return 0;
seph2pos(time,seph,rs,dts,var);
time=timeadd(time,tt);
seph2pos(time,seph,rst,dtst,var);
*svh=seph->svh;
}
else return 0;
// 在信号发射时刻的基础上给定一个微小的时间间隔,再次计算新时刻的 P、V、C。与3结合,通过扰动法计算出卫星的速度和频漂。
// 并没有使用那些位置和钟差公式对时间求导的结果
/* satellite velocity and clock drift by differential approx */
for (i=0;i<3;i++) rs[i+3]=(rst[i]-rs[i])/tt; // 卫星速度rs[i+3]
dts[1]=(dtst[0]-dts[0])/tt; // 钟漂dts[1]
return 1;
}
1. eph2pos():
extern void eph2pos(gtime_t time, const eph_t *eph, double *rs, double *dts,
double *var)
{
double tk,M,E,Ek,sinE,cosE,u,r,i,O,sin2u,cos2u,x,y,sinO,cosO,cosi,mu,omge;
double xg,yg,zg,sino,coso;
int n,sys,prn;
trace(4,"eph2pos : time=%s sat=%2d\n",time_str(time,3),eph->sat);
if (eph->A<=0.0) { //通过卫星轨道半长轴 A 判断星历是否有效,无效则返回
rs[0]=rs[1]=rs[2]=*dts=*var=0.0;
return;
}
tk=timediff(time,eph->toe); //计算规化时间 tk (E.4.2)
switch ((sys=satsys(eph->sat,&prn))) { //根据不同卫星系统设置相应的地球引力常数 mu 和 地球自转角速度 omge
case SYS_GAL: mu=MU_GAL; omge=OMGE_GAL; break;
case SYS_CMP: mu=MU_CMP; omge=OMGE_CMP; break;
default: mu=MU_GPS; omge=OMGE; break;
}
M=eph->M0+(sqrt(mu/(eph->A*eph->A*eph->A))+eph->deln)*tk; //计算平近点角 M (E.4.3)
//用牛顿迭代法来计算偏近点角 E。参考 RTKLIB manual P145 (E.4.19) (E.4.4)
for (n=0,E=M,Ek=0.0;fabs(E-Ek)>RTOL_KEPLER&&n<MAX_ITER_KEPLER;n++) {
Ek=E; E-=(E-eph->e*sin(E)-M)/(1.0-eph->e*cos(E));
}
if (n>=MAX_ITER_KEPLER) {
trace(2,"eph2pos: kepler iteration overflow sat=%2d\n",eph->sat);
return;
}
sinE=sin(E); cosE=cos(E);
trace(4,"kepler: sat=%2d e=%8.5f n=%2d del=%10.3e\n",eph->sat,eph->e,n,E-Ek);
//计算摄动改正后的 升交点角距u 卫星矢径长度r 轨道倾角i
u=atan2(sqrt(1.0-eph->e*eph->e)*sinE,cosE-eph->e)+eph->omg; //(E.4.5) (E.4.6) (E.4.10)
r=eph->A*(1.0-eph->e*cosE); //(E.4.11)
i=eph->i0+eph->idot*tk; //(E.4.12)
sin2u=sin(2.0*u); cos2u=cos(2.0*u);
u+=eph->cus*sin2u+eph->cuc*cos2u; //(E.4.7)
r+=eph->crs*sin2u+eph->crc*cos2u; //(E.4.8)
i+=eph->cis*sin2u+eph->cic*cos2u; //(E.4.9)
x=r*cos(u); y=r*sin(u);
cosi=cos(i);
// 北斗的MEO、IGSO卫星计算方法与GPS, Galileo and QZSS相同,只是一些参数不同
// GEO卫星的 O 和最后位置的计算稍有不同
/* beidou geo satellite */
if (sys==SYS_CMP&&(prn<=5||prn>=59)) { /* ref [9] table 4-1 */
O=eph->OMG0+eph->OMGd*tk-omge*eph->toes; //(E.4.29)
sinO=sin(O); cosO=cos(O);
xg=x*cosO-y*cosi*sinO;
yg=x*sinO+y*cosi*cosO;
zg=y*sin(i);
sino=sin(omge*tk); coso=cos(omge*tk);
rs[0]= xg*coso + yg*sino*COS_5 + zg*sino*SIN_5; //ECEF位置(E.4.30)
rs[1]=-xg*sino + yg*coso*COS_5 + zg*coso*SIN_5;
rs[2]=-yg*SIN_5 + zg*COS_5;
}
else {
O=eph->OMG0+(eph->OMGd-omge)*tk-omge*eph->toes; //计算升交点赤经O (E.4.13)
sinO=sin(O); cosO=cos(O);
rs[0]=x*cosO-y*cosi*sinO; //计算卫星ECEF位置存入 rs 中 (E.4.14)
rs[1]=x*sinO+y*cosi*cosO;
rs[2]=y*sin(i);
}
tk=timediff(time,eph->toc); //(E.4.15)
*dts=eph->f0+eph->f1*tk+eph->f2*tk*tk; //利用三个二项式模型系数 af0、af1、af2计算卫星钟差
/* relativity correction */
*dts-=2.0*sqrt(mu*eph->A)*eph->e*sinE/SQR(CLIGHT); //相对论效应改正卫星钟差
/* position and clock error variance */
*var=var_uraeph(sys,eph->sva); //用 URA 值来标定方差
}
2. var_uraeph():用URA用户测距精度标定卫星位置方差
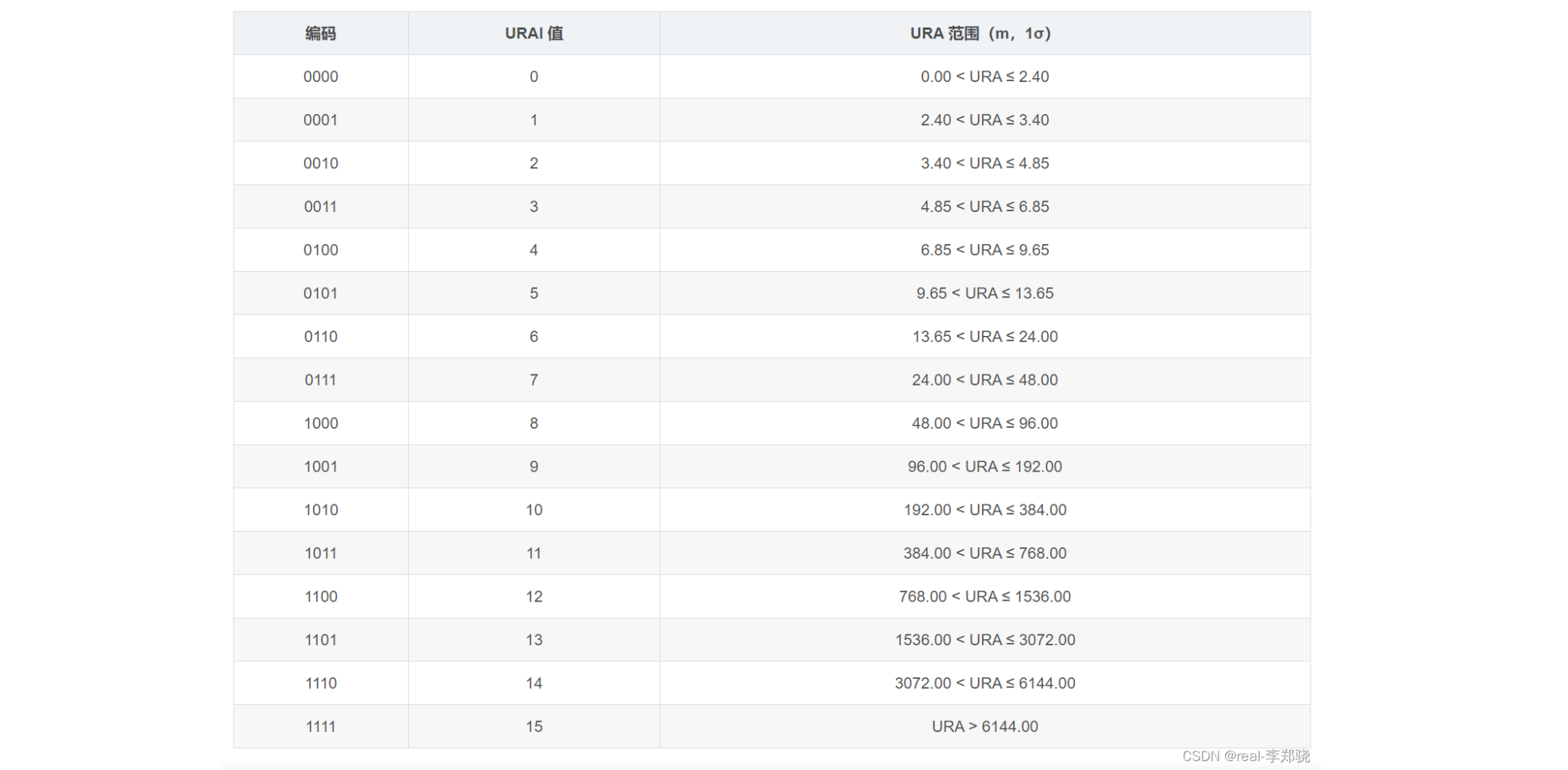
GLONASS 不计算,直接定位 5*5
static double var_uraeph(int sys, int ura)
{
const double ura_value[]={
2.4,3.4,4.85,6.85,9.65,13.65,24.0,48.0,96.0,192.0,384.0,768.0,1536.0,
3072.0,6144.0
};
if (sys==SYS_GAL) { /* galileo sisa (ref [7] 5.1.11) */
if (ura<= 49) return SQR(ura*0.01);
if (ura<= 74) return SQR(0.5+(ura- 50)*0.02);
if (ura<= 99) return SQR(1.0+(ura- 75)*0.04);
if (ura<=125) return SQR(2.0+(ura-100)*0.16);
return SQR(STD_GAL_NAPA);
}
else { /* gps ura (ref [1] 20.3.3.3.1.1) */
return ura<0||14<ura?SQR(6144.0):SQR(ura_value[ura]);
}
}
3. geph2pos():由 GLONASS 星历计算卫星位置钟差
GLONASS 卫星播发的是 PZ-90 坐标系下参考时刻的卫星状态向量,每半个小时广播一次。如果需要得到某个时间的卫星位置必须通过运动模型积分得到。
extern void geph2pos(gtime_t time, const geph_t *geph, double *rs, double *dts,
double *var)
{
double t,tt,x[6];
int i;
trace(4,"geph2pos: time=%s sat=%2d\n",time_str(time,3),geph->sat);
t=timediff(time,geph->toe);
*dts=-geph->taun+geph->gamn*t; // 计算钟差dts(E.4.26)
for (i=0;i<3;i++) {
x[i ]=geph->pos[i];
x[i+3]=geph->vel[i];
}
//步长 TSTEP:60s
for (tt=t<0.0?-TSTEP:TSTEP;fabs(t)>1E-9;t-=tt) {
if (fabs(t)<TSTEP) tt=t;
glorbit(tt,x,geph->acc);
}
for (i=0;i<3;i++) rs[i]=x[i];
*var=SQR(ERREPH_GLO); // glonass卫星的方差直接定为 5*5
}
4. glorbit():龙格库塔迭代
y n + 1 = y n + h 6 ( k 1 + 2 k 2 + 2 k 3 + k 4 ) k 1 = f ( y n ) k 2 = f ( y n + k 1 h 2 ) k 3 = f ( y n + k 2 h 2 ) k 4 = f ( y n + k 3 h ) \begin{aligned} \mathrm{y}_{\mathrm{n}+1} & =\mathrm{y}_{\mathrm{n}}+\frac{\mathrm{h}}{6}\left(\mathrm{k}_{1}+2 \mathrm{k}_{2}+2 \mathrm{k}_{3}+\mathrm{k}_{4}\right) \\ \mathrm{k}_{1} & =\mathrm{f}\left(\mathrm{y}_{\mathrm{n}}\right) \\ \mathrm{k}_{2} & =\mathrm{f}\left(\mathrm{y}_{\mathrm{n}}+\mathrm{k}_{1} \frac{\mathrm{h}}{2}\right) \\ \mathrm{k}_{3} & =\mathrm{f}\left(\mathrm{y}_{\mathrm{n}}+\mathrm{k}_{2} \frac{\mathrm{h}}{2}\right) \\ \mathrm{k}_{4} & =\mathrm{f}\left(\mathrm{y}_{\mathrm{n}}+\mathrm{k}_{3} \mathrm{~h}\right)\end{aligned} yn+1k1k2k3k4=yn+6h(k1+2k2+2k3+k4)=f(yn)=f(yn+k12h)=f(yn+k22h)=f(yn+k3 h)
5. deq():微分方程计算
d x d t = v x , d y d t = v y , d z d t = v z d v x d t = − μ r 3 x − 3 2 J 2 μ a e 2 r 5 x ( 1 − 5 z 2 r 2 ) + ω e 2 x + 2 ω e v y + a x d v y d t = − μ r 3 y − 3 2 J 2 μ a e 2 r 5 y ( 1 − 5 z 2 r 2 ) + ω e 2 y − 2 ω e v x + a y d v z d t = − μ r 3 z − 3 2 J 2 μ a e 2 r 5 z ( 3 − 5 z 2 r 2 ) + a z \begin{array}{l}\frac{d x}{d t}=v_{x}, \frac{d y}{d t}=v_{y}, \frac{d z}{d t}=v_{z} \\ \frac{d v_{x}}{d t}=-\frac{\mu}{r^{3}} x-\frac{3}{2} J_{2} \frac{\mu a_{e}^{2}}{r^{5}} x\left(1-\frac{5 z^{2}}{r^{2}}\right)+\omega_{e}^{2} x+2 \omega_{e} v_{y}+a_{x} \\ \frac{d v_{y}}{d t}=-\frac{\mu}{r^{3}} y-\frac{3}{2} J_{2} \frac{\mu a_{e}^{2}}{r^{5}} y\left(1-\frac{5 z^{2}}{r^{2}}\right)+\omega_{e}^{2} y-2 \omega_{e} v_{x}+a_{y} \\ \frac{d v_{z}}{d t}=-\frac{\mu}{r^{3}} z-\frac{3}{2} J_{2} \frac{\mu a_{e}^{2}}{r^{5}} z\left(3-\frac{5 z^{2}}{r^{2}}\right)+a_{z}\end{array} dtdx=vx,dtdy=vy,dtdz=vzdtdvx=−r3μx−23J2r5μae2x(1−r25z2)+ωe2x+2ωevy+axdtdvy=−r3μy−23J2r5μae2y(1−r25z2)+ωe2y−2ωevx+aydtdvz=−r3μz−23J2r5μae2z(3−r25z2)+az
其中:
- a e a_{e} ae : earth semi-major axis ( 6378136.0 m ) (6378136.0 \mathrm{~m}) (6378136.0 m)
- μ \mu μ : earth gravitational constant ( 398600.44 × 1 0 9 m 3 / s 2 ) \left(398600.44 \times 10^{9} \mathrm{~m}^{3} / \mathrm{s}^{2}\right) (398600.44×109 m3/s2)
- ω e \omega_{e} ωe : earth angular velocity ( 7.292115 × 1 0 − 5 r a d / s ) \left(7.292115 \times 10^{-5} \mathrm{rad} / \mathrm{s}\right) (7.292115×10−5rad/s)
- J 2 J_{2} J2 : second zonal harmonic of the geopotential ( 1082625.7 × 1 0 − 9 ) \left(1082625.7 \times 10^{-9}\right) (1082625.7×10−9)
- r = x 2 + y 2 + z 2 r=\sqrt{x^{2}+y^{2}+z^{2}} r=x2+y2+z2
4、peph2pos():精密星历计算卫星位置、钟差、速度、钟漂

-
调用
pephpos()根据精密星历计算卫星位置,其中先二分查找时间最接近的精密星历,然后地球自转改正,调用interppol()内维尔插值获取卫星位置、线性插值获取钟差,最后计算标准差。 -
调用
pephclk()根据精密星历计算卫星钟差,其中先二分查找时间最接近的精密钟差,再线性插值获取钟差、计算标准差。 -
计算相对论效应改正量,调用
satantoff()计算卫星天线相位偏差改正。加上改正量得到卫星位置钟差。 -
加上一个极小的时间,再计算一次位置,两次计算出的时间作差求得卫星速度钟飘。
-
调用
satantoff()天线相位中心改正。 -
钟差做相对论效应改正:
d T s ( t ) = ( t i + 1 − t ) d T s ( t i ) + ( t − t i ) d T s ( t i + 1 ) t i + 1 − t i − 2 r s ( t ) T v s ( t ) c 2 d T^{s}(t)=\frac{\left(t_{i+1}-t\right) d T^{s}\left(t_{i}\right)+\left(t-t_{i}\right) d T^{s}\left(t_{i+1}\right)}{t_{i+1}-t_{i}}-2 \frac{\boldsymbol{r}^{s}(t)^{T} \boldsymbol{v}^{s}(t)}{c^{2}} dTs(t)=ti+1−ti(ti+1−t)dTs(ti)+(t−ti)dTs(ti+1)−2c2rs(t)Tvs(t)
extern int peph2pos(gtime_t time, int sat, const nav_t *nav, int opt,
double *rs, double *dts, double *var)
{
double rss[3],rst[3],dtss[1],dtst[1],dant[3]={0},vare=0.0,varc=0.0,tt=1E-3;
int i;
if (sat<=0||MAXSAT<sat) return 0;
// 调用 pephpos() 根据精密星历计算卫星位置
// 调用 pephclk() 根据精密星历计算卫星钟差
/* satellite position and clock bias */
if (!pephpos(time,sat,nav,rss,dtss,&vare,&varc)||
!pephclk(time,sat,nav,dtss,&varc)) return 0;
// 加上一个极小的时间,再计算一次位置,两次计算出的时间作差求得卫星速度钟飘
time=timeadd(time,tt);
if (!pephpos(time,sat,nav,rst,dtst,NULL,NULL)||
!pephclk(time,sat,nav,dtst,NULL)) return 0;
// 调用 satantoff() 天线相位中心改正
/* satellite antenna offset correction */
if (opt) {
satantoff(time,rss,sat,nav,dant);
}
for (i=0;i<3;i++) {
rs[i ]=rss[i]+dant[i];
rs[i+3]=(rst[i]-rss[i])/tt;
}
// 钟差做相对论效应改正
/* relativistic effect correction */
if (dtss[0]!=0.0) {
dts[0]=dtss[0]-2.0*dot(rs,rs+3,3)/CLIGHT/CLIGHT;
dts[1]=(dtst[0]-dtss[0])/tt;
}
else /* no precise clock */
dts[0]=dts[1]=0.0;
*var=vare+varc;
return 1;
}
1. 精密星历读取流程
nav->peph[]存精密星历数据,nav->ne精密钟差数量。
nav->pclk[]存精密钟差数据,nav->nc精密钟差数量。
- execses_b() 中调用
readpreceph()。 - readpreceph() 中:
readsp3()读取精密星历,readrnxc()读取精密钟差 - readsp3() 中:
readsp3h()读文件头,readsp3b()读文件体,combpeph()对精密星历按时间、index 排序,再将相同星历合并。 - readrnxc() 中:
readrnxfile()读取精密星历文件,combpclk()排序合并精密钟差。
2. pephpos():精密星历计算卫星位置,钟差
执行流程如下:
3. interppol():Neville 插值
Neville 算法是一种计算插值多项式方法,由给定的 n+1个节点,存在一个唯一的幂次 ≤n 的多项式存在,并且通过给定点;所以可以由两个 n-1 次插值多项式构造一个 n 次多项式的线性逐次插值。给定
n
+
1
\mathrm{n}+1
n+1 个节点及其对应函数值
(
x
i
,
y
i
)
\left(x_{i}, y_{i}\right)
(xi,yi) ,假设
P
i
,
j
P_{i, j}
Pi,j 表示
j
−
i
j-i
j−i 阶多项式,并且满足通过节点
(
x
k
,
y
k
)
k
=
i
,
i
+
1
,
⋯
,
j
\left(x_{k}, y_{k}\right) \quad k=i, i+1, \cdots, j
(xk,yk)k=i,i+1,⋯,j 。
P
i
,
j
P_{i, j}
Pi,j 满足以下迭代关系:
p
i
,
i
(
x
)
=
y
i
P
i
,
j
(
x
)
=
(
x
j
−
x
)
p
i
,
j
−
1
(
x
)
+
(
x
−
x
i
)
p
i
+
1
,
j
(
x
)
x
j
−
x
i
,
0
≤
i
≤
j
≤
n
\begin{array}{l} p_{i, i}(x)=y_{i} \\ P_{i, j}(x)=\frac{\left(x_{j}-x\right) p_{i, j-1}(x)+\left(x-x_{i}\right) p_{i+1, j}(x)}{x_{j}-x_{i}}, \quad 0 \leq i \leq j \leq n \end{array}
pi,i(x)=yiPi,j(x)=xj−xi(xj−x)pi,j−1(x)+(x−xi)pi+1,j(x),0≤i≤j≤n
以
n
=
4
n=4
n=4 的节点举例,其迭代过程为:
p
1
,
1
(
x
)
=
y
1
p
2
,
2
(
x
)
=
y
2
,
p
1
,
2
(
x
)
p
3
,
3
(
x
)
=
y
3
,
p
2
,
3
(
x
)
,
p
1
,
3
(
x
)
p
4
,
4
(
x
)
=
y
4
,
p
3
,
4
(
x
)
,
p
2
,
4
(
x
)
,
p
1
,
4
(
x
)
\begin{array}{l} p_{1,1}(x)=y_{1} \\ p_{2,2}(x)=y_{2}, p_{1,2}(x) \\ p_{3,3}(x)=y_{3}, p_{2,3}(x), p_{1,3}(x) \\ p_{4,4}(x)=y_{4}, p_{3,4}(x), p_{2,4}(x), p_{1,4}(x) \end{array}
p1,1(x)=y1p2,2(x)=y2,p1,2(x)p3,3(x)=y3,p2,3(x),p1,3(x)p4,4(x)=y4,p3,4(x),p2,4(x),p1,4(x)
static double interppol(const double *x, double *y, int n)
{
int i,j;
for (j=1;j<n;j++) {
for (i=0;i<n-j;i++) {
y[i]=(x[i+j]*y[i]-x[i]*y[i+1])/(x[i+j]-x[i]);
}
}
return y[0];
}
4. posWithEarhRotation():
static void posWithEarhRotation(const int k, double pos[3], double p[3][NMAX+1], double dt)
{
double sinl,cosl;
#if 0
p[0][k]=pos[0];
p[1][k]=pos[1];
#else
/* correciton for earh rotation ver.2.4.0 */
sinl=sin(OMGE*dt);
cosl=cos(OMGE*dt);
p[0][k]=cosl*pos[0]-sinl*pos[1];
p[1][k]=sinl*pos[0]+cosl*pos[1];
#endif
p[2][k]=pos[2];
}
5. pephclk():精密钟差计算卫星钟差
简单的线性插值:
d
T
s
(
t
)
=
(
t
i
+
1
−
t
)
d
T
s
(
t
i
)
+
(
t
−
t
i
)
d
T
s
(
t
i
+
1
)
t
i
+
1
−
t
i
d T^{s}(t)=\frac{\left(t_{i+1}-t\right) d T^{s}\left(t_{i}\right)+\left(t-t_{i}\right) d T^{s}\left(t_{i+1}\right)}{t_{i+1}-t_{i}}
dTs(t)=ti+1−ti(ti+1−t)dTs(ti)+(t−ti)dTs(ti+1)
IGS 的精密钟差计算完之后,需要考虑相对论效应的影响:
d
T
s
(
t
)
=
(
t
i
+
1
−
t
)
d
T
s
(
t
i
)
+
(
t
−
t
i
)
d
T
s
(
t
i
+
1
)
t
i
+
1
−
t
i
−
2
r
s
(
t
)
T
v
s
(
t
)
c
2
d T^{s}(t)=\frac{\left(t_{i+1}-t\right) d T^{s}\left(t_{i}\right)+\left(t-t_{i}\right) d T^{s}\left(t_{i+1}\right)}{t_{i+1}-t_{i}}-2 \frac{\boldsymbol{r}^{s}(t)^{T} \boldsymbol{v}^{s}(t)}{c^{2}}
dTs(t)=ti+1−ti(ti+1−t)dTs(ti)+(t−ti)dTs(ti+1)−2c2rs(t)Tvs(t)
三、rescode():残差计算、设计矩阵构建
计算当前迭代的伪距残差 v、设计矩阵 H、伪距残差的方差 var、所有观测卫星的方位角和仰角 azel,定位时有效性 vsat、定位后伪距残差 resp、参与定位的卫星个数 ns 和方程个数 nv
int iter I 迭代次数,在estpos()里迭代调用,第i次迭代就传i
int bElevCVG I
obsd_t *obs I 观测量数据
int n I 观测量数据的数量
double *rs I 卫星位置和速度,长度为6*n,{x,y,z,vx,vy,vz}(ecef)(m,m/s)
double *dts I 卫星钟差,长度为2*n, {bias,drift} (s|s/s)
double *vare I 卫星位置和钟差的协方差 (m^2)
int *svh I 卫星健康标志 (-1:correction not available)
nav_t *nav I 导航数据
double *x I 本次迭代开始之前的定位值,7*1,前3个是本次迭代开始之前的定位值,第4个是钟差,后三个分别是gps系统与glonass、galileo、bds系统的钟差。
prcopt_t *opt I 处理过程选项
double *v O 定位方程的右端部分,伪距残差
double *H O 定位方程中的几何矩阵
double *var O 参与定位的伪距残差的方差
double *azel O 对于当前定位值,所有观测卫星的 {方位角、高度角} (2*n)
int *vsat O 所有观测卫星在当前定位时是否有效 (1*n)
double *resp O 所有观测卫星的伪距残差,(P-(r+c*dtr-c*dts+I+T)) (1*n)
int *ns O 参与定位的卫星的个数
int *bDeleted O

-
将之前得到的定位解信息赋值给
rr和dtr数组。 -
调用
ecef2pos()将将接收机位置rr由 ECEF-XYZ 转换为大地坐标系LLHpos -
遍历当前历元所有
OBS[],即遍历每颗卫星:-
将
vsat[]、azel[]和resp[]数组置 0,因为在前后两次定位结果中,每颗卫星的上述信息都会发生变化。time赋值OBS的时间,sat赋值OBS的卫星。 -
检测当前观测卫星是否和下一个相邻数据重复;重复则不处理这一条,continue去处理下一条。
-
调用
satexclude()函数判断卫星是否需要排除,如果排除则continue去处理下一个卫星。 -
调用
geodist()函数,计算卫星和当前接收机位置之间的几何距离r和接收机到卫星的方向向量e。 -
调用
satazel()函数,计算在接收机位置处的站心坐标系中卫星的方位角和仰角;若仰角低于截断值opt->elmin,continue不处理此数据。 -
调用
snrmask(),根据接收机高度角和信号频率来检测该信号是否可用。 -
调用
ionocorr()函数,计算电离层延时I,所得的电离层延时是建立在 L1 信号上的,当使用其它频率信号时,依据所用信号频组中第一个频率的波长与 L1 波长的比率,对上一步得到的电离层延时进行修正。 -
调用
tropcorr()函数,计算对流层延时T。 -
调用
prange()函数,计算经过DCB校正后的伪距值p。 -
计算伪距残差
v[nv],即经过钟差,对流层,电离层改正后的伪距。 -
组装设计矩阵
H
h ( x ) = ( ρ r 1 + c d t r − c d T 1 + I r 1 + T r 1 ρ r 2 + c d t r − c d T 2 + I r 2 + T r 2 ρ r 3 + c d t r − c d T 3 + I r 3 + T r s 3 ⋮ ρ r m + c d t r − c d T m + I r m + T r m ) H = ( − e r 1 T 1 − e r 2 T 1 − e r 3 T 1 ⋮ ⋮ − e r m T 1 ) \boldsymbol{h}(\boldsymbol{x})=\left(\begin{array}{c}\rho_{r}^{1}+c d t_{r}-c d T^{1}+I_{r}^{1}+T_{r}^{1} \\ \rho_{r}^{2}+c d t_{r}-c d T^{2}+I_{r}^{2}+T_{r}^{2} \\ \rho_{r}^{3}+c d t_{r}-c d T^{3}+I_{r}^{3}+T_{r}^{s 3} \\ \vdots \\ \rho_{r}^{m}+c d t_{r}-c d T^{m}+I_{r}^{m}+T_{r}^{m}\end{array}\right) \boldsymbol{H}=\left(\begin{array}{cc}-e_{r}^{1 T} & 1 \\ -e_{r}^{2 T} & 1 \\ -e_{r}^{3 T} & 1 \\ \vdots & \vdots \\ -e_{r}^{m T} & 1\end{array}\right) h(x)= ρr1+cdtr−cdT1+Ir1+Tr1ρr2+cdtr−cdT2+Ir2+Tr2ρr3+cdtr−cdT3+Ir3+Trs3⋮ρrm+cdtr−cdTm+Irm+Trm H= −er1T−er2T−er3T⋮−ermT111⋮1 -
处理不同系统(GPS、GLO、GAL、CMP)之间的时间偏差,修改矩阵
H。 -
调用
varerr()函数,计算此时的导航系统误差 -
为了防止不满秩的情况,把矩阵
H补满秩了,H[j+nv*NX]=j==i+3?1.0:0.0;
-
static int rescode(const int iter, int bElevCVG, const obsd_t *obs, int n, const double *rs, const double *dts,
const double *vare, const int *svh, const nav_t *nav, const double *x, const prcopt_t *opt,
double *v, double *H, double *var, double *azel, int *vsat, double *resp, int *nx, int *bDeleted)
{
int bObserved[5];
int i,j,nv=0,ns[5]={0},sys,satsn[MAXOBS],sat;
double r,dion,dtrp,vion,vtrp,rr[3],pos[3],dtr,e[3],P,elev_t[MAXSAT],vmeas,lam_L1;
double elmin;
int bMulGNSS;
*nx=NX_SPP;
for (i=0;i<5;i++) {bObserved[i]=0; ns[i]=0;}
for (i=0;i<n;i++) v[i]=var[i]=0.0;
for (i=0;i<NX_SPP*(n+5);i++) H[i]=0.0;
for (i=0;i<MAXSAT;i++) elev_t[i]=0.0;
//将之前得到的定位解信息赋值给 rr 和 dtr 数组,以进行关于当前解的伪距残差的相关计算
for (i=0;i<3;i++) rr[i]=x[i]; dtr=x[3];
// rr{x,y,z}->pos{lat,lon,h}
ecef2pos(rr,pos);
// 遍历当前历元观测值
for (i=0;i<n&&i<MAXOBS;i++) {
sat=obs[i].sat; // sat 赋值 OBS 的卫星
vsat[i]=0; azel[i*2]=azel[1+i*2]=resp[i]=0.0;
sys=PPP_Glo.sFlag[sat-1].sys;
// 如果这颗卫星 bDeleted 被排除了,或者卫星系统没使用,跳过当前观测值不处理
if (bDeleted[sat-1]==0) continue;
if (!(sys&opt->navsys)) continue;
// 去除重复观测值
/* reject duplicated observation data */
if (i<n-1&&i<MAXOBS-1&&obs[i].sat==obs[i+1].sat) {
sprintf(PPP_Glo.chMsg,"*** WARNING: duplicated observation data %s sat=%2d\n",
time_str(obs[i].time,3),obs[i].sat);
outDebug(OUTWIN,OUTFIL,0);
i++;
continue;
}
// 调用 geodist() 计算近似几何距离
// 调用 satazel() 计算方位角高度角,剔除高度角过低的卫星观测值
/* geometric distance/azimuth/elevation angle */
if ((r=geodist(rs+i*6,rr,e))<=0.0) continue; // 近似几何距离小于 0,排除
satazel(pos,e,azel+i*2);
if (bElevCVG) {
if (PPP_Glo.prcOpt_Ex.bElevCheckEx) { // 如果启用了高度角检查,截止高度角不能小于两度
elmin=0.0;
elmin=MIN(opt->elmin,2.0*D2R);
elmin=MAX(opt->elmin/3.0,elmin);
if (azel[1+i*2]<elmin) continue; // 高度角小于设截止高度角,排除
}
else {
if (azel[1+i*2]<opt->elmin) continue;
}
}
else {
if (azel[1+i*2]<=0.0)
azel[1+i*2]=MIN(3.0*D2R,opt->elmin*0.75);
if (iter>=1) {
if (azel[1+i*2]<opt->elmin) continue;
}
}
// 调用 prange() 码偏差改正,得到改正后的伪距 P,如果设置了消电离层组合直接得到组合后的伪距 P
/* psudorange with code bias correction */
if ((P=prange(obs+i,nav,azel+i*2,opt,&vmeas))==0.0) continue;
// 调用 satexclude() 排除不可用卫星的观测值
/* excluded satellite */
if (satexclude(obs[i].sat,svh[i],opt)) continue;
// 调用 ionocorr() 克罗布歇电离层改正,计算 L1 信号上计算电离层延时 I
// 当使用其它频率信号时,依据所用信号频组中第一个频率的波长与 L1 波长的关系,对上一步得到的电离层延时进行修正
/* ionospheric corrections */
if (!ionocorr(obs[i].time,sys,nav,pos,azel+i*2,opt,&dion,&vion)) continue;
/* GPS-L1 -> L1/B1 */
if ((lam_L1=nav->lam[obs[i].sat-1][0])>0.0) {
dion*=SQR(lam_L1/lam_carr[0]);
}
// 调用 tropcorr() Saastamoinen 对流层改正
/* tropospheric corrections */
if (!tropcorr(obs[i].time,nav,pos,azel+i*2,opt,&dtrp,&vtrp)) continue;
// 构建残差向量 V = P-(r+c*dtr-c*dts+I+T) (E.6.31)
/* pseudorange residual */
v[nv]=resp[i]=P-(r+dtr-CLIGHT*dts[i*2]+dion+dtrp);
// 构建设计矩阵 H,前 3 行为中计算得到的视线向,第 4 行为 1,其它行为 0
/* design matrix */
for (j=0;j<4;j++) H[j+nv*NX_SPP]=j<3?-e[j]:1.0;
// 修改矩阵 H,处理不同系统(GPS、GLO、GAL、CMP)之间的时间偏差
/* time system and receiver bias offset */
if (sys==SYS_GLO) {v[nv]-=x[4]; H[4+nv*NX_SPP]=1.0; ns[1]++; bObserved[1]=1;}
else if (sys==SYS_CMP) {v[nv]-=x[5]; H[5+nv*NX_SPP]=1.0; ns[2]++; bObserved[2]=1;}
else if (sys==SYS_GAL) {v[nv]-=x[6]; H[6+nv*NX_SPP]=1.0; ns[3]++; bObserved[3]=1;}
else if (sys==SYS_QZS) {v[nv]-=x[7]; H[7+nv*NX_SPP]=1.0; ns[4]++; bObserved[4]=1;}
else {H[4+nv*NX_SPP]=H[5+nv*NX_SPP]=0.0; ns[0]++; bObserved[0]=1;}
vsat[i]=1; resp[i]=v[nv];
satsn[nv]=obs[i].sat;
elev_t[sat-1]=azel[1+i*2]*R2D;
// 调用 varerr() 函数,计算此时的导航系统误差,然后累加计算用户测距误差(URE)
/* error variance */
var[nv]=varerr(opt,azel[1+i*2],sys)+vare[i]+vion+vtrp;
if (azel[1+i*2]<opt->elmin) var[nv]*=100.0;
nv++;
}
for (i=j=0;i<5;i++) {
if (bObserved[i]) j++;
}
bMulGNSS=0;
if (j>=2) bMulGNSS=1;
// 调用 getHVR_spp(),获取 HVR
i=nv;
nv=getHVR_spp(bMulGNSS,iter,opt->navsys,bElevCVG,bDeleted,satsn,H,v,var,elev_t,nv,*nx);
for (i=0;i<5;i++) {
if (ns[i]>0) continue;
for (j=0;j<nv;j++)
H[(3+i)+j*(*nx)]=0.0;
}
for (i=0;i<5;i++) {
if (ns[i]==0) *nx=*nx-1;
}
//*nx=*nx-1;
return nv;
// v 和 resp 的主要区别在于长度不一致
// v 是需要参与定位方程组的解算的,维度为 nv*1;
// resp 仅表示所有观测卫星的伪距残余,维度为 n*1,对于没有参与定位的卫星,该值为 0
}
1、geodist():计算近似几何距离、接收机到卫星方向的观测矢量,sagnac 效应改正
地球自转引起的误差是信号传输过程中 GNSS 卫星信号发射时刻和接收机接收到信号的时刻之间地球自转对 GNSS 观测值产生的影响。相当于地球自转使得卫星空间位置在信号播发、收到的过程中接收机在地固系坐标轴上相对于 Z \mathrm{Z} Z 轴发生了一定角度的旋转,使得 GNSS 卫星的在信号发射时刻的位置发生了变化,也称为 Sagnac 效应。
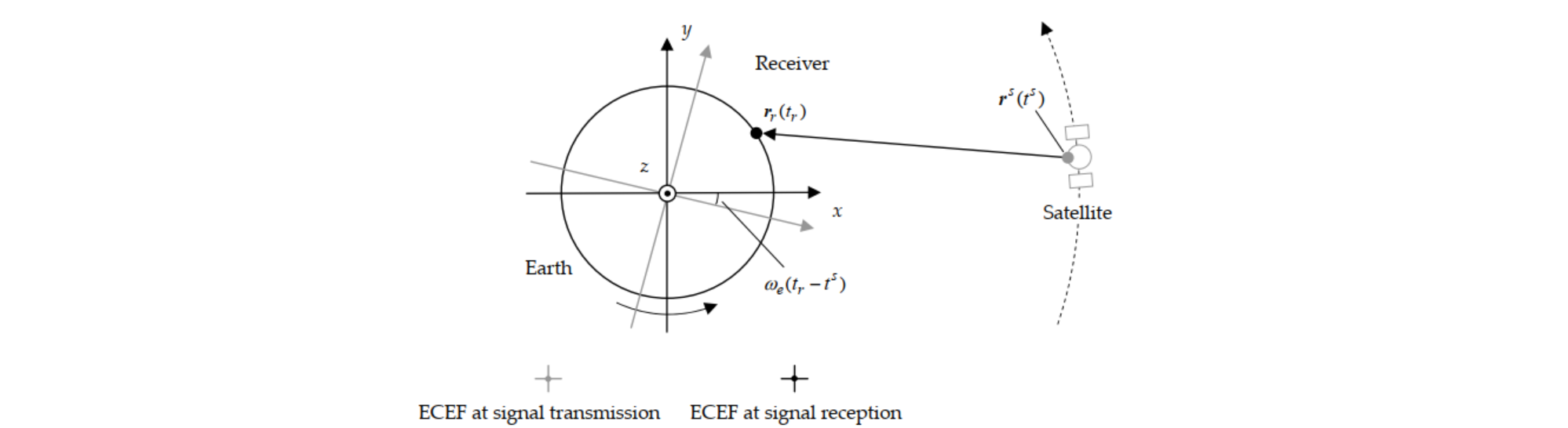
地球自转引起的距离改正公式如下:
[
x
s
′
y
s
s
′
z
s
′
]
=
[
cos
ω
τ
sin
ω
τ
0
−
sin
ω
τ
cos
ω
τ
0
0
0
1
]
[
x
s
y
s
z
s
]
δ
sagnac,
r
,
j
=
ω
e
c
(
x
s
y
r
−
y
s
x
r
)
\begin{array}{c}{\left[\begin{array}{l}x^{s^{\prime}} \\ y^{s^{s^{\prime}}} \\ z^{s^{\prime}}\end{array}\right]=\left[\begin{array}{ccc}\cos \omega \tau & \sin \omega \tau & 0 \\ -\sin \omega \tau & \cos \omega \tau & 0 \\ 0 & 0 & 1\end{array}\right]\left[\begin{array}{l}x^{s} \\ y^{s} \\ z^{s}\end{array}\right]} \\ \delta_{\text {sagnac, } r, j}=\frac{\omega_{e}}{c}\left(x^{s} y_{r}-y^{s} x_{r}\right)\end{array}
xs′yss′zs′
=
cosωτ−sinωτ0sinωτcosωτ0001
xsyszs
δsagnac, r,j=cωe(xsyr−ysxr)
上式中
(
x
s
′
,
y
s
′
,
z
s
′
)
\left(x^{s^\prime}, y^{s^{\prime}}, z^{s^{\prime}}\right)
(xs′,ys′,zs′) 为地球自旋转后卫星的坐标值,
(
x
s
,
y
s
,
z
s
)
\left(x^{s}, y^{s}, z^{s}\right)
(xs,ys,zs) 为地球自旋转前卫星的坐标值,
ω
e
\omega_{e}
ωe 代表地球自传角速度值,
τ
\tau
τ 为卫星发射信号时刻到接收机接收卫星时刻的历元数。
改正地球自转后的近似几何距离近似几何距离如下:
ρ
r
s
≈
∥
r
r
(
t
r
)
−
r
s
(
t
s
)
∥
+
ω
e
c
(
x
s
y
r
−
y
s
x
r
)
\begin{array}{l} \rho_{r}^{s} \approx\left\|\boldsymbol{r}_{r}\left(t_{r}\right)-\boldsymbol{r}^{s}\left(t^{s}\right)\right\|+\frac{\omega_{e}}{c}\left(x^{s} y_{r}-y^{s} x_{r}\right) \end{array}
ρrs≈∥rr(tr)−rs(ts)∥+cωe(xsyr−ysxr)
接收机到卫星方向的观测矢量计算公式如下:
e
r
s
=
r
s
(
t
s
)
−
r
r
(
t
r
)
∥
r
s
(
t
s
)
−
r
r
(
t
r
)
∥
\boldsymbol{e}_{r}^{s}=\frac{\boldsymbol{r}^{s}\left(t^{s}\right)-\boldsymbol{r}_{r}\left(t_{r}\right)}{\left\|\boldsymbol{r}^{s}\left(t^{s}\right)-\boldsymbol{r}_{r}\left(t_{r}\right)\right\|}
ers=∥rs(ts)−rr(tr)∥rs(ts)−rr(tr)
对应的代码如下,传入 ECEF 卫星坐标 rs、接收机近似 ECEF 坐标 rr,计算之后近似几何距离做返回值返回,观测矢量做参数三 e 返回:
extern double geodist(const double *rs, const double *rr, double *e)
{
double r;
int i;
if (norm(rs,3)<RE_WGS84) return -1.0; // 检查卫星到 WGS84坐标系原点的距离是否大于基准椭球体的长半径。
for (i=0;i<3;i++) e[i]=rs[i]-rr[i]; // 求卫星和接收机坐标差e[]
r=norm(e,3); // 求未经萨格纳克效应改正的距离
for (i=0;i<3;i++) e[i]/=r; // 接收机到卫星的单位向量e[] (E.3.9)
return r+OMGE*(rs[0]*rr[1]-rs[1]*rr[0])/CLIGHT; //(E.3.8b)
}
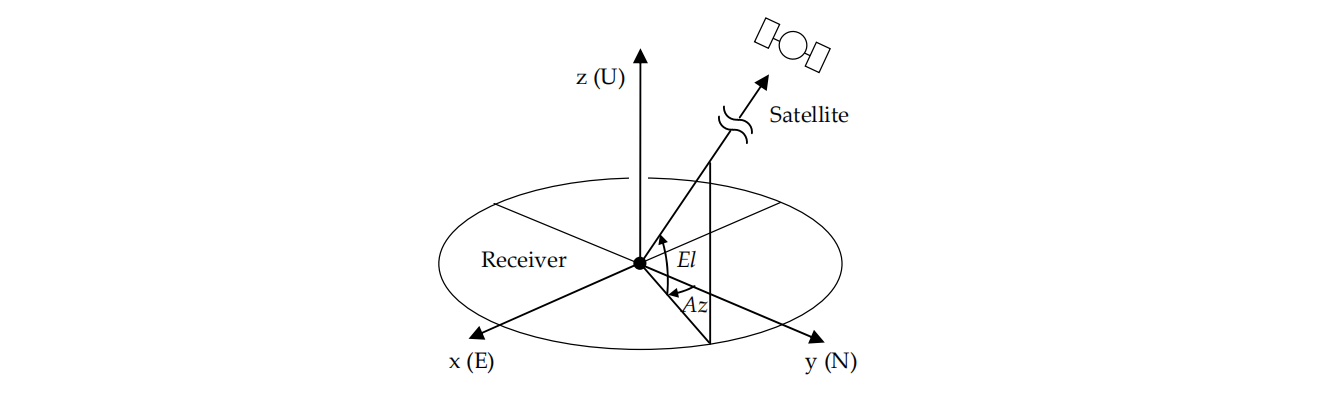
2、satazel():计算方位角高度角
方位角范围在
[
0
,
2
π
]
[0,2 \pi]
[0,2π],高度角范围在
[
−
π
2
,
π
2
]
[-\frac{\pi}{2},\frac{\pi}{2}]
[−2π,2π];以接收机为原点,建立站心坐标系 ENU,根据卫星 ENU 下方向矢量可以得到高度角、方位角,公式如下:
e
r
,
enu
s
=
E
r
e
r
s
=
(
e
e
,
e
n
,
e
u
)
T
A
z
r
s
=
ATAN
2
(
e
e
,
e
n
)
E
l
r
s
=
arcsin
(
e
u
)
\begin{array}{l}\boldsymbol{e}_{r, \text { enu }}^{s}=\boldsymbol{E}_{r} \boldsymbol{e}_{r}^{s}=\left(e_{e}, e_{n}, e_{u}\right)^{T} \\ A z_{r}^{s}=\operatorname{ATAN} 2\left(e_{e}, e_{n}\right) \\ E l_{r}^{s}=\arcsin \left(e_{u}\right)\end{array}
er, enu s=Erers=(ee,en,eu)TAzrs=ATAN2(ee,en)Elrs=arcsin(eu)
对应的代码如下,传入接收机 LLH 坐标 pos、接收机到卫星方向的观测矢量 e,计算之后返回弧度制的高度角,如果传了参三 azel,那么 azel[0] 是方位角、azel[1] 是高度角。
extern double satazel(const double *pos, const double *e, double *azel)
{
double az=0.0,el=PI/2.0,enu[3];
if (pos[2]>-RE_WGS84) {
ecef2enu(pos,e,enu);
az=dot(enu,enu,2)<1E-12?0.0:atan2(enu[0],enu[1]);
if (az<0.0) az+=2*PI;
el=asin(enu[2]);
}
if (azel) {azel[0]=az; azel[1]=el;}
return el;
}
3、prange():差分码偏差改正
DCB 差分码偏差,针对伪距,是由不同类型的 GNSS 信号在卫星和接收机不同通道产生的时间延迟(硬件延迟/码偏差)差异 。由于卫星播发的测距码类型很多, C1、 P1、 P2 等 ,不同的测距信号虽然在同一台卫星钟的驱动下生成的,因而花费的时间也不同。我们把卫星钟脉冲驱动下开始生成测距信号至信号生成并最终离开卫星发射天线相位中心之间所花费的时间称为信号在卫星内部的时延。DCB 体现的就是不同码信号时延的差。分为:
- 频内偏差:相同频率不同码之间存在的偏差(如 P1-C1、P2-C2 等)
- 频间偏差:不同频率之间存在的偏差(如 P1-P2)
一般来说接收机端的DCB被接收机钟差所吸收,可以跟接收机钟差一起解算。若需提高定位精度,卫星端的码偏差需进行校正。目前,码偏差产品主要分为 2 类:① 广播星历播发的时间群延迟(time group delay,TGD)产品;② IGS分析中心提供的高精度后处理差分码偏差(differential code bias,DCB)产品。因此,TGD 产品相比于 DCB 产品,精度低于 DCB 产品且适用于实时场景。DCB 与 TGD 直接计算的关系如下:
T
G
D
=
1
1
−
γ
D
C
B
12
T G D=\frac{1}{1-\gamma} D C B_{12}
TGD=1−γ1DCB12
D C B 12 = ( 1 − γ ) × T G D D C B_{12}=(1-\gamma) \times T G D DCB12=(1−γ)×TGD
对于 GPS 而言,其广播星历及精密星历是采用 P1、P2 无电离层组合进行卫星钟差估计。因此,广播星历钟差及精密星历钟差均包含 P1、P2 无电离层组合的硬件延迟。当用户基于 P1、P2 无电离层组合定位解算时,无需考虑硬件延迟;反之,若用户使用 P1、P2 单频或其他组合时,均需要考虑硬件延迟的影响,否则会影响定位解算的精度。
若用户使用 C/A 码,用户需借助外部文件获取 P-C 将 C/A 码归化到 P 码,然后再进行 TGD/DCB 改正。
与 GPS 不同,BDS 广播星历的钟差基准参考 B3 频点,多数机构的精密钟差基准是 B1/B3 无电离层组合。
4、gettgd():
static double gettgd(int sat, const nav_t *nav, double *tgd1, double *tgd2)
{
int i;
for (i=0;i<nav->n;i++) {
if (nav->eph[i].sat!=sat) continue;
// 如果是北斗
if (PPP_Glo.sFlag[sat-1].sys==SYS_CMP) {
if (tgd1) *tgd1=CLIGHT*nav->eph[i].tgd[0];
if (tgd2) *tgd2=CLIGHT*nav->eph[i].tgd[1];
return CLIGHT*(nav->eph[i].tgd[0]);
}
// 群波延迟参数 * 光速
return CLIGHT*nav->eph[i].tgd[0];
}
return 0.0;
}
4、satexclude():排除不可用卫星的观测值
- 卫星健康标志
svh< 0,排除。 - 根据
opt->exsats[sat-1]判断是否使用了该卫星。 - 根据
opt->navsys判断是否使用了该卫星系统。
extern int satexclude(int sat, int svh, const prcopt_t *opt)
{
int sys=PPP_Glo.sFlag[sat-1].sys;
// 卫星健康标志 svh < 0:排除
if (svh<0) return 1; /* ephemeris unavailable */
if (opt) {
// 根据 opt->exsats[sat-1] 判断是否使用了该卫星
if (opt->exsats[sat-1]==1) return 1; /* excluded satellite */
if (opt->exsats[sat-1]==2) return 0; /* included satellite */
// 根据 opt->navsys 判断是否使用了该卫星系统
if (!(sys&opt->navsys)) return 1; /* unselected sat sys */
}
if (sys==SYS_QZS) svh&=0xFE; /* mask QZSS LEX health */
if (svh) {
sprintf(PPP_Glo.chMsg,"*** WARNING: unhealthy satellite: sat=%3d svh=%02X\n",sat,svh);
outDebug(0,0,0);
return 1;
}
return 0;
}
5、ionocorr():根据选项模型计算 L1 电离层延迟 I
受太阳辐射的影响,距地面 60km 以上的大气层处于部分电离或完全电离状态,该区域被称为电离层。当电磁波信号通过电离层时,传播速度和传播路径会发生改变,给 GNSS 观测值带来误差,即电离层延迟。电离层延迟大小由电子密度和信号频率决定,影响可达数十米。电离层延迟与单位面积的横截面在信号传播路径上拦截的电子总量
N
e
N_e
Ne 成正比,且与载波频率
f
f
f 的平方成反比,弥散性的电离层降低了测距码的传播速度,而加快了载波相位的传播速度,如下所示:
I
=
I
ρ
=
−
I
ϕ
=
40.28
N
e
f
2
I=I_ \rho=-I_\phi=40.28\frac{N_e}{f^2}
I=Iρ=−Iϕ=40.28f2Ne
在一些条件下,可使用经验模型改正或约束观测值中的电离层延迟,常用的电离层延迟经验模型有 Klobuchar 模型、Bent 模型和电离层格网模型等。
可以总结出电离层几个对于解算有用的特点:
- 对伪距和载波影响相反:UOFC 组合,但伪距载波之间延迟
- 与频率有关:消电离层组合,但放大噪声
- 延迟与电子总量 TEC 成正比:建立电离层格网模型 TEC 文件电离层改正,或者将 STEC 作为参数估计。
static int ionocorr(gtime_t time, const int sys, const nav_t *nav, const double *pos,
const double *azel, const prcopt_t *opt, double *ion,
double *var)
{
// 克罗布歇模型(广播星历模型)
/* broadcast model */
if (opt->ionoopt==IONOOPT_BRDC) {
//*ion=ionmodel(time,nav->ion_gps,pos,azel);
if (sys==SYS_GPS) *ion=ionmodel(time,nav->ion_gps,pos,azel);
//else if ( SYS_CMP==sys ) *ion=ionmodel(time,nav->ion_cmp,pos,azel);
else *ion=ionmodel(time,nav->ion_gps,pos,azel);
*var=SQR(*ion*ERR_BRDCI);
return 1;
}
// 电离层格网模型
/* ionex tec model */
else if (opt->ionoopt==IONOOPT_TEC) {
return iontec(time,nav,pos,azel,3,ion,var);
}
// IF 消电离层组合
else if (opt->ionoopt==IONOOPT_IF12) {
*ion=0.0;
*var=SQR(0.02);
return 1;
}
*ion=0.0;
*var=opt->ionoopt==IONOOPT_OFF?SQR(ERR_ION):0.0;
return 1;
}
6、ionmodel():克罗布歇模型电离层延迟计算
SPP 中使用克罗布歇模型计算 L1 的电离层改正量,将晚间的电离层时延视为常数,取值为 5ns,把白天的时延看成是余弦函数中正的部分。于是天顶方向调制在 L1 载波上的测距码的电离层时延可表示为:
T
g
=
5
×
1
0
−
9
+
A
cos
2
π
P
(
t
−
1
4
h
)
T_{g}=5 \times 10^{-9}+A \cos \frac{2 \pi}{P}\left(t-14^{h}\right)
Tg=5×10−9+AcosP2π(t−14h)
振幅
A
A
A 和周期
P
P
P 分别为:
A
=
∑
i
=
0
3
α
i
(
φ
m
)
i
P
=
∑
i
=
0
3
β
i
(
φ
m
)
i
\begin{array}{l} A=\sum_{i=0}^{3} \alpha_{i}\left(\varphi_{m}\right)^{i} \\ P=\sum_{i=0}^{3} \beta_{i}\left(\varphi_{m}\right)^{i} \end{array}
A=∑i=03αi(φm)iP=∑i=03βi(φm)i
全球定位系统向单频接收机用户提供的电离层延迟改正时就采用上述模型。其中
α
i
\alpha_i
αi 和
β
i
\beta_i
βi 是地面控制系统根据该天为一年中的第几天(将一年分为 37 个区间)以及前 5 天太阳的平均辐射流量(共分10档)从 370 组常数中选取的,然后编入星导航电文播发给用户。卫星在其播发的导航电文中提供了这 8 个电离层延迟参数:
p
ion
=
(
α
0
,
α
1
,
α
2
,
α
3
,
β
0
,
β
1
,
β
2
,
β
3
)
T
p_{\text {ion }}=\left(\alpha_{0}, \alpha_{1}, \alpha_{2}, \alpha_{3}, \beta_{0}, \beta_{1}, \beta_{2}, \beta_{3}\right)^{T}
pion =(α0,α1,α2,α3,β0,β1,β2,β3)T
根据根据参数
α
0
,
α
1
,
α
2
,
α
3
\alpha_0,\alpha_1,\alpha_2,\alpha_3
α0,α1,α2,α3 确定振幅
A
A
A,根据根据参数
β
0
,
β
1
,
β
2
,
β
3
\beta_0,\beta_1,\beta_2,\beta_3
β0,β1,β2,β3 确定周期
T
T
T,再给定一个以秒为单位的当地时间
t
t
t,就能算出天顶电离层延迟。再由天顶对流层延迟根据倾斜率转为卫星方向对流层延迟。
电离层分布在离地面 60-1000km 的区域内。当卫星不在测站的天顶时,信号传播路径上每点的地方时和纬度均不相同,为了简化计算,我们将整个电离层压缩为一个单层,将整个电离层中的自由电子都集中在该单层上,用它来代替整个电离层。这个电离层就称为中心电离层。中心电离层离地面的高度通常取 350km。式中的参数 t t t 和式中的参数 φ m \varphi_{m} φm 分别为卫星言号传播路径与中心电离层的交点 P ′ P^{\prime} P′ 的时角和地磁纬度,因为只有 P ′ P^{\prime} P′ 才能反映卫星信号所受到的电离层延迟的总的情况。
综上,已知大地经度、 大地纬度、卫星的高度角和卫星测站的方位角,电离层延迟计算方法如下:
计算测站
P
P
P 和
P
′
P^{\prime}
P′ 在地心的夹角:
ψ
=
0.0137
/
(
E
l
+
0.11
)
−
0.022
\psi=0.0137 /(E l+0.11)-0.022
ψ=0.0137/(El+0.11)−0.022
计算交点
P
′
P^{\prime}
P′ 的地心纬度:
φ
i
=
φ
+
ψ
cos
A
z
\varphi_{i}=\varphi+\psi \cos A z
φi=φ+ψcosAz
{ φ l > + 0.416 φ l = + 0.416 φ l > − 0.416 φ l = − 0.416 \left\{\begin{array}{ll}\varphi_{l}>+0.416 & \varphi_{l}=+0.416 \\ \varphi{l}>-0.416 & \varphi_{l}=-0.416\end{array}\right. {φl>+0.416φl>−0.416φl=+0.416φl=−0.416
计算交点
P
′
P^{\prime}
P′ 的地心经度:
λ
i
=
λ
+
ψ
sin
A
z
/
cos
φ
i
\lambda_{i}=\lambda+\psi \sin A z / \cos \varphi_{i}
λi=λ+ψsinAz/cosφi
计算地磁纬度:
φ
m
=
φ
i
+
0.064
cos
(
λ
i
−
1.617
)
\varphi_{m}=\varphi_{i}+0.064 \cos \left(\lambda_{i}-1.617\right)
φm=φi+0.064cos(λi−1.617)
计算观测瞬间交点
P
′
P^{\prime}
P′ 处的地方时:
t
=
4.32
×
1
0
4
λ
i
+
t
t=4.32 \times 10^{4} \lambda_{i}+t
t=4.32×104λi+t
{ t > 86400 t = t − 86400 t < 0 t = t + 86400 \left\{\begin{array}{ll}t>86400 & t=t-86400 \\ t<0 & t=t+86400\end{array}\right. {t>86400t<0t=t−86400t=t+86400
计算倾斜因子:
F
=
1.0
+
16.0
×
(
0.53
−
E
l
)
3
F=1.0+16.0 \times(0.53-E l)^{3}
F=1.0+16.0×(0.53−El)3
计算电离层时间延迟:
x
=
2
π
(
t
−
50400
)
/
∑
n
=
0
3
β
n
φ
m
n
I
r
s
=
{
F
×
5
×
1
0
−
9
F
×
(
5
×
1
0
−
9
+
∑
n
=
1
4
α
n
φ
m
n
×
(
1
−
x
2
2
+
x
4
24
)
)
(
∣
x
∣
>
1.57
)
\begin{array}{l}x=2 \pi(t-50400) / \sum_{n=0}^{3} \beta_{n} \varphi_{m}{ }^{n} \\ I_{r}^{s}=\left\{\begin{array}{cc}F \times 5 \times 10^{-9} \\ F \times\left(5 \times 10^{-9}+\sum_{n=1}^{4} \alpha_{n} \varphi_{m}{ }^{n} \times\left(1-\frac{x^{2}}{2}+\frac{x^{4}}{24}\right)\right) & (|x|>1.57)\end{array}\right.\end{array}
x=2π(t−50400)/∑n=03βnφmnIrs={F×5×10−9F×(5×10−9+∑n=14αnφmn×(1−2x2+24x4))(∣x∣>1.57)
计算的是 L1 信号的电离层延时 I ,当使用其它频率信号时,依据所用信号频组中第一个频率的波长与 L1 波长的比例关系,对上一步得到的电离层延时进行修正,不考虑模糊度情况下改正公式为:
I
=
Φ
2
−
Φ
1
1
−
(
f
1
/
f
2
)
2
I=\frac{\Phi_{2}-\Phi_{1}}{1-\left(f_{1} / f_{2}\right)^{2}}
I=1−(f1/f2)2Φ2−Φ1
extern double ionmodel(gtime_t t, const double *ion, const double *pos,
const double *azel)
{
const double ion_default[]={ /* 2004/1/1 */
0.1118E-07,-0.7451E-08,-0.5961E-07, 0.1192E-06,
0.1167E+06,-0.2294E+06,-0.1311E+06, 0.1049E+07
};
double tt,f,psi,phi,lam,amp,per,x;
int week;
if (pos[2]<-1E3||azel[1]<=0) return 0.0;
if (norm(ion,8)<=0.0) ion=ion_default; //若没有电离层参数,用默认参数
/* earth centered angle (semi-circle) */ //地球中心角
psi=0.0137/(azel[1]/PI+0.11)-0.022; //计算地心角(E.5.6)
/* subionospheric latitude/longitude (semi-circle) */
phi=pos[0]/PI+psi*cos(azel[0]); //计算穿刺点地理纬度(E.5.7)
if (phi> 0.416) phi= 0.416; //phi不超出(-0.416,0.416)范围
else if (phi<-0.416) phi=-0.416;
lam=pos[1]/PI+psi*sin(azel[0])/cos(phi*PI); //计算穿刺点地理经度(E.5.8)
/* geomagnetic latitude (semi-circle) */
phi+=0.064*cos((lam-1.617)*PI); //计算穿刺点地磁纬度(E.5.9)
/* local time (s) */
tt=43200.0*lam+time2gpst(t,&week); //计算穿刺点地方时(E.5.10)
tt-=floor(tt/86400.0)*86400.0; /* 0<=tt<86400 */
/* slant factor */
f=1.0+16.0*pow(0.53-azel[1]/PI,3.0); //计算投影系数(E.5.11)
/* ionospheric delay */
amp=ion[0]+phi*(ion[1]+phi*(ion[2]+phi*ion[3]));
per=ion[4]+phi*(ion[5]+phi*(ion[6]+phi*ion[7]));
amp=amp< 0.0? 0.0:amp;
per=per<72000.0?72000.0:per;
x=2.0*PI*(tt-50400.0)/per; //(E.5.12)
return CLIGHT*f*(fabs(x)<1.57?5E-9+amp*(1.0+x*x*(-0.5+x*x/24.0)):5E-9); //(E.5.13)
}
7、tropcorr():对流层改正
对流层一般指距离地面 50km 内的大气层,是大气层质量的主要部分。当导航信号穿过对流层时,由于传播介质密度的增加,信号传播路径和传播速度会发生改变,由此引起的 GNSS 观测值误差称为对流层延迟。对流层延迟一般可分为干延迟和湿延迟,对于载波相位和伪距完全相同,一般在米级大小,可通过模型改正和参数估计的方法来削弱其影响。修正模型如下:
T
=
M
d
r
y
T
d
r
y
+
M
w
e
t
T
w
e
t
T=M_{d r y} T_{d r y}+M_{w e t} T_{w e t}
T=MdryTdry+MwetTwet
式中,
T
d
r
y
,
T
w
e
t
T_{d r y}, T_{w e t}
Tdry,Twet 分别表示接收机天顶对流层的干延迟和湿延迟;
M
d
r
y
,
M
w
e
t
M_{d r y}, M_{w e t}
Mdry,Mwet 分别表示干延迟和湿延迟的投影函数。对流层干延迟比较稳定,主要与测站高度、大气温度和大气压相关,可通过模型改正,常用模型有 Saastamoninen 模型、Hopfield 模型等。湿延迟不同于干延迟,变化较大,主要与水汽含量相关,一般估计天顶对流层湿延迟,通过投影函数计算各卫星的电离层湿延迟,常用的投影函数有全球投影函数(Global Mapping Function,GMF)、Niell 投影函数(NMF)和 Vienna投影函数(Vienna Mapping Function,VMF)等。
可以总结出电离层几个对于解算有用的特点:
-
非弥散介质:对所有卫星的信号影响相同。
-
分干湿延迟:
8、tropmodel():Saastamoinen 模型计算对流层延迟
p = 1013.25 × ( 1 − 2.2557 × 1 0 − 5 h ) 5.2568 T = 15.0 − 6.5 × 1 0 − 3 h + 273.15 e = 6.108 × exp { 17.15 T − 4684.0 T − 38.45 } × h r e l 100 \begin{array}{l}p=1013.25 \times\left(1-2.2557 \times 10^{-5} h\right)^{5.2568} \\ T=15.0-6.5 \times 10^{-3} h+273.15 \\ e=6.108 \times \exp \left\{\frac{17.15 T-4684.0}{T-38.45}\right\} \times \frac{h_{r e l}}{100}\end{array} p=1013.25×(1−2.2557×10−5h)5.2568T=15.0−6.5×10−3h+273.15e=6.108×exp{T−38.4517.15T−4684.0}×100hrel
T r s = 0.002277 cos z { p + ( 1255 T + 0.05 ) e − tan 2 z } T_{r}^{s}=\frac{0.002277}{\cos z}\left\{p+\left(\frac{1255}{T}+0.05\right) e-\tan ^{2} z\right\} Trs=cosz0.002277{p+(T1255+0.05)e−tan2z}
其中 z z z 是天顶角,与高度角互余: z = π / 2 − E l r s z=\pi / 2-E l_{r}^{s} z=π/2−Elrs
7、varerr():计算伪距量测协方差
σ 2 = F s R r ( a σ 2 + b σ 2 / sin E l r s ) + σ eph 2 + σ ion 2 + σ trop 2 + σ bias 2 \begin{array}{l} \sigma^{2}=F^{s} R_{r}\left(a_{\sigma}{ }^{2}+b_{\sigma}{ }^{2} / \sin E l_{r}^{s}\right)+{\sigma_{\text {eph }}}^{2}+{\sigma_{\text {ion }}}^{2}+{\sigma_{\text {trop }}}^{2}+{\sigma_{\text {bias }}}^{2}\end{array} σ2=FsRr(aσ2+bσ2/sinElrs)+σeph 2+σion 2+σtrop 2+σbias 2
其中:
- F s F^{s} Fs:卫星系统误差因子,GLONASS 1.5,SBAS fact 3,其它 1。
- R r R_{r} Rr:
- a σ , b σ a_{\sigma}, b_{\sigma} aσ,bσ:
- σ e p h \sigma_{e p h} σeph:
- σ ion \sigma_{\text {ion }} σion :
- σ trop \sigma_{\text {trop }} σtrop :
- σ bias \sigma_{\text {bias }} σbias :
varerr() 函数只计算了第一项:
static double varerr(const prcopt_t *opt, double el, int sys)
{
double fact,varr;
fact=sys==SYS_GLO?PPP_Glo.prcOpt_Ex.errRatioGLO:(sys==SYS_CMP?PPP_Glo.prcOpt_Ex.errRatioBDS:
(sys==SYS_GAL?PPP_Glo.prcOpt_Ex.errRatioGAL:(sys==SYS_QZS?PPP_Glo.prcOpt_Ex.errRatioQZS:opt->err[0])));
varr=(SQR(opt->err[1])+SQR(opt->err[2])/sin(el)); // sin(el) 多了方,疑似bug
if (opt->ionoopt==IONOOPT_IF12) varr*=SQR(3.0); /* iono-free */ //消电离层组合,方差*3*3
return SQR(fact)*varr;
}
后面的对流层、电离层、星历误差在 rescode() 中加入:
var[nv]=varerr(opt,azel[1+i*2],sys)+vare[i]+vion+vtrp;
8、getHVR_spp
四、lsqplus():最小二乘估计
最小二乘准则为:
V
T
P
V
=
min
V^{T} P V=\min
VTPV=min
最小二乘的一般观测模型和误差方程如下所示:
{
L
n
×
1
=
B
n
×
t
X
t
×
1
+
d
n
×
1
x
t
×
1
=
X
t
×
1
−
X
0
,
t
×
1
l
n
×
1
=
L
n
×
1
−
(
B
n
×
t
X
0
,
t
×
1
+
d
n
×
1
)
V
n
×
1
=
B
n
×
1
x
t
×
1
−
l
n
×
1
,
P
n
×
n
\left\{\begin{array}{l} L_{n \times 1}=B_{n \times t} X_{t \times 1}+d_{n \times 1} \\ x_{t \times 1}=X_{t \times 1}-X_{0, t \times 1} \\ l_{n \times 1}=L_{n \times 1}-\left(B_{n \times t} X_{0, t \times 1}+d_{n \times 1}\right) \\ V_{n \times 1}=B_{n \times 1} x_{t \times 1}-l_{n \times 1}, P_{n \times n} \end{array}\right.
⎩
⎨
⎧Ln×1=Bn×tXt×1+dn×1xt×1=Xt×1−X0,t×1ln×1=Ln×1−(Bn×tX0,t×1+dn×1)Vn×1=Bn×1xt×1−ln×1,Pn×n