【面试经典150 | 栈】逆波兰表达式求值

文章目录

写在前面
Tag
题目来源
题目解读
解题思路
- 方法一：栈
- 方法二：使用数组模拟栈
知识点拨
- 两个概念
- 中缀表达式转后缀表达式
- 后缀表达式计算四则运算表达式
- 例题
写在最后

写在前面

本专栏专注于分析与讲解【面试经典150】算法，两到三天更新一篇文章，欢迎催更……

专栏内容以分析题目为主，并附带一些对于本题涉及到的数据结构等内容进行回顾与总结，文章结构大致如下，部分内容会有增删：

Tag：介绍本题牵涉到的知识点、数据结构；
题目来源：贴上题目的链接，方便大家查找题目并完成练习；
题目解读：复述题目（确保自己真的理解题目意思），并强调一些题目重点信息；
解题思路：介绍一些解题思路，每种解题思路包括思路讲解、实现代码以及复杂度分析；
知识回忆：针对今天介绍的题目中的重点内容、数据结构进行回顾总结。

Tag

【逆波兰】【后缀表达式】【栈】

题目来源

150. 逆波兰表达式求值

题目解读

计算逆波兰表达式表示的算术表达式的结果。

解题思路

逆波兰表达式是一种后缀表达式，所谓后缀就是指算符写在后面。

平常使用的算式则是一种中缀表达式，如 ( 1 + 2 ) * ( 3 + 4 ) 。
该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。

逆波兰表达式主要有以下两个优点：

去掉括号后表达式无歧义，上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
适合用栈操作运算：遇到数字则入栈；遇到运算符则取出栈顶两个数字进行计算，并将结果压入栈中。

以下将介绍两种方法来解决本题，本质上都是使用栈操作，方法一中直接使用栈，方法二我们利用数组模拟栈。

方法一：栈

定义一个栈 stk，栈中存放 int 整型数字。遍历字符串数组：

遇到数字字符将数字字符转化成 int 整型数字存放在栈中；
遇到运算符，就将栈顶两个数字出栈，执行相应的运算符操作。

我们在遍历字符串数组的时候，需要将字符型数字转化成整型数字，在 C++ 中有两种方法：

stoi()：将字符串型数字转化成整型数字；
atoi()：将字符型数字转化成整型数字。

实现代码

class Solution {
public:
    bool isNumber(string& str) {
        return !(str == "+" || str == "-" || str == "*" || str == "/");
    }

    int evalRPN(vector<string>& tokens) {
        stack<int> stk;
        for (auto token : tokens) {
            if (isNumber(token)) {
                stk.push(atoi(token.c_str()));
            }
            else {
                int num2 = stk.top(); stk.pop();
                int num1 = stk.top(); stk.pop();
                switch(token[0]) {
                    case '+':
                        stk.push(num1 + num2);
                        break;
                    case '-':
                        stk.push(num1 - num2);
                        break;
                    case '*':
                        stk.push(num1 * num2);
                        break;
                    case '/':
                        stk.push(num1 / num2);
                        break;
                }
            }
        }
        return stk.top();
    }
};

复杂度分析

时间复杂度： $O (n)$ ， $n$ 为字符串数组的长度。

空间复杂度： $O (n)$ 。

方法二：使用数组模拟栈

我们可以使用数组来模拟栈。本方法参考自。

使用数组的话需要首先定义数组的长度。对于长度为 $n$ 的逆波兰表达式， $n$ 一定为奇数，表达式中的操作数的个数一定比运算符多一个，即操作数有 $\frac{n+1}{2}$ 个，运算符有 $\frac{n-1}{2}$ 个。我们遍历逆波兰表达式：

如果遇到操作数，则将操作数入栈，因此栈内元素增加 1 个；
如果遇到运算符，则将两个操作数出栈，然后将一个新操作数入栈，因此栈内元素先减少 2 个再增加 1 个，结果是栈内元素减少 1 个。

具体实现中，我们创建一个数组 stack 模拟栈，数组下标 0 的位置对应栈底，定义 idx 对应栈顶元素的下标，初始时栈为空，idx = -1。遇到操作数和运算符时，进行如下操作：

如果遇到操作符，则 idx 加一，然后将操作数赋值给 stack[idx]；
如果遇到运算符，则 idx 减一，此时的 stack[idx] 和 stack[idx+1] 分别是左操作数和右操作数，使用运算符对两个操作数进行运算，将运算得到的新操作数赋给 stack[idx]。

遍历完整个逆波兰表达式后，栈中只剩下一个元素，表现在数组 stack 中就是 idx = 0，最后返回 stack[idx] 即为逆波兰表达式的值。

实现代码

class Solution {
public:
    int evalRPN(vector<string>& tokens) {
        int n = tokens.size();
        vector<int> stack((n + 1) / 2);
        int idx = -1;
        for (auto token : tokens) {
            if (token.size() > 1 || isdigit(token[0])) {
                ++idx;
                stack[idx] = atoi(token.c_str());
            }
            else {
                switch(token[0]) {
                    case '+':
                        --idx;
                        stack[idx] += stack[idx + 1];
                        break;
                    case '-':
                        --idx;
                        stack[idx] -= stack[idx + 1];
                        break;
                    case '*':
                        --idx;
                        stack[idx] *= stack[idx + 1];
                        break;
                    case '/':
                        --idx;
                        stack[idx] /= stack[idx + 1];
                        break;
                }
            }        
        }
        return stack[idx];
    }
};

复杂度分析

时间复杂度： $O (n)$ ，其中 $n$ 是数组 tokens 的长度。需要遍历数组 tokens 一次，计算逆波兰表达式的值。

空间复杂度： $O (n)$ 。需要创建长度为 $\frac{n+1}{2}$ 的数组模拟栈操作。

知识点拨

我们来看一下如何使用栈来计算四则运算表达式，通常利用栈来计算四则运算表达式需要先将四则元素表达式即中缀表达式转化成后缀表达式，然后利用后缀表达式来求计算结果。

我们先来看一个中缀表达式和后缀表达式的概念。

两个概念

中缀表达式，中缀表达式就是我们平常所说的 “四则运算表达式” ，形象的说明就是运算符号分布在两个数字中间。
后缀表达式，后缀表达式就是，形如 “9 3 1 - 3 * + 10 2 / +” 这样形式的，运算符号都出现在运算数字之后的形式。

中缀表达式转后缀表达式

在明确了一些基本的概念之后，我们就可以来看看如何将中缀表达式转后缀表达式。

维护一个栈作为辅助工具，维护一个字符串数组作为输出的后缀表达式。从左到右依次遍历中缀表达式中的字符：

若是数字就是直接输出到数组中，成为后缀表达式的一部分；
若是符号则进行如下判断：
- 当前符号是右括号则栈顶元素依次出栈；
- 当前符号优先级低于栈顶符号，或者一致，则出栈；
- 当前符号入栈。
重复上述，过程直至最后输出后缀表达式。

后缀表达式计算四则运算表达式

这个问题，在题目中已经详细讲解过了，这里就不再解释了。

例题

用栈来计算标准四则运算表达式 $(12 - 3) /3 + 2 * 3$ 的值。

一般来说，不会让你求一个中缀表达式的后缀表达式，更多的考察形式是给你一个后缀表达式让你对应对应中缀表达式的值。

接下来将以图解的形式来看一下中缀转后缀和利用后缀计算表达式值的过程。

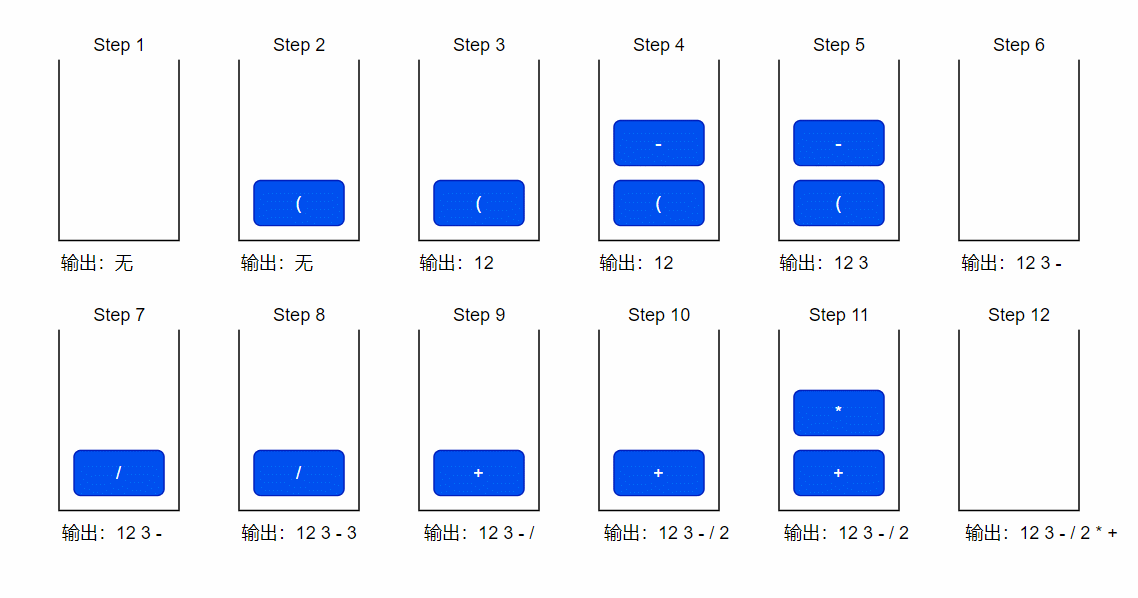
中缀表达式转后缀表达式

中缀转后缀用栈示意图

1 初始化一个空栈，用来运算符号进出栈使用

2 开始遍历中缀表达式，第一个符号是左括号直接入栈

3 当前字符是 “12” 是数字，直接输出

4 第三个字符是 ”-“ 是运算符号，入栈

5 第四个字符是运算数字，直接输出

6 接着的字符是右括号，匹配前面的左括号，因此将栈顶依次出栈直至遇到左括号为止，将出栈的符号依次输出

7 栈空了， $\div$ 直接入栈

8 遇到运算数字，直接输出

9 当前符号是运算符号 “+” ，优先级低于栈顶元素， $\div$ 出栈并输出，”+“ 入栈

10 遇到数字，直接输出

11 当前符号是运算符号 $\times$ ，优先级并不比栈顶符号优先级低或者等于，符号直接入栈

12 遇到数字直接入栈，中缀表达式遍历完毕，栈内符号依次出栈，最终输出后缀表达式 $\space 3 - 3 \space \div \space 2 \space 3 \space \times \space +$ .

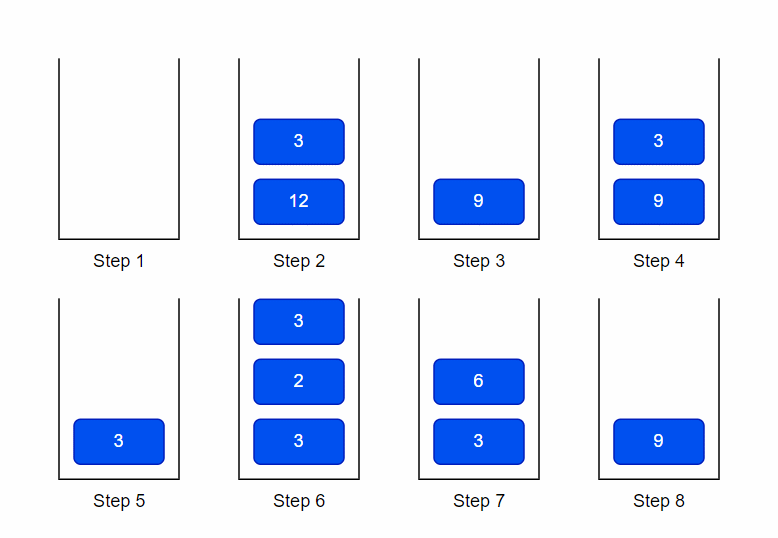
利用后缀表达式计算

后缀计算用栈示意图

1 维护一个空栈，用来存放运算数字

2 遇到数字直接入栈

3 遇到运算符号 $-$ ，出栈得到减数 3 ，再次出栈得到被减数 12 ，两数相减得到 9，入栈

4 遇到数字直接入栈

5 遇到运算符号 $\div$ ，出栈得到除数 3 ，再次出栈得到被除数 9 ，两数相除得到 3，入栈

6 遇到数字直接入栈

7 遇到运算符号 $\times$ ，出栈得到乘数 3 ，再次出栈得到乘数 2 ，两数乘得到 6，入栈

8 遇到运算符号 $+$ ，所以将 6 与 3 出栈并相加，得到 9，并入栈

结果为 9 出栈，栈为空。