C++哈希表：一种快速查找和插入的方法

文章目录

1、前言
2、unordered系列关联式容器
- 2.1、 unordered_map
- - 2.1.1、unordered_map的文档介绍
  - 2.1.2、unordered_map的接口说明
- 2.2、 unordered_set
3. 底层结构
- 3.1 哈希概念
- 3.2 哈希冲突
- 2.3 哈希函数
- 2.4 哈希冲突解决
- - 2.4.1 闭散列
  - 2.4.2 开散列
4. 模拟实现
- 4.1 哈希表的改造
- 4.2 unordered_map
5、哈希的应用
- 5.1 位图
- - 5.1.1 位图概念
  - 5.1.2 位图的实现
  - 5.1.3 位图的应用
- 5.2 布隆过滤器
- - 5.2.1 布隆过滤器提出
  - 5.2.2布隆过滤器概念
  - 5.2.3 布隆过滤器的插入
  - 5.2.4 布隆过滤器的查找
  - 5.2.5 布隆过滤器删除
  - 5.2.6 布隆过滤器优点
  - 5.2.7 布隆过滤器缺陷

1、前言

哈希表是一种非常重要的数据结构，它在各种场合中都有广泛的应用。在C++中，哈希表通常是通过标准模板库(STL)中的unordered_map或unordered_set来实现的。本篇文章将向读者介绍哈希表的基本概念、原理、实现方法以及优化策略。通过掌握哈希表，我们可以实现高效的查找和插入操作。

2、unordered系列关联式容器

在C++98标准中，STL提供了底层数据结构为红黑树的一系列关联式容器，例如map、set、multimap和multiset等。这些关联式容器在查询操作中的效率可以达到 $log_2 N$ ，也就是说，在最坏的情况下，我们只需要比较红黑树的高度次就可以找到目标元素。然而，当树中的节点数量非常多时，查询效率可能会变得不太理想。为了追求更高的查询效率，C++11标准中引入了四个unordered系列的关联式容器，分别是unordered_map、unordered_set、unordered_multimap和unordered_multiset。这些容器与红黑树结构的关联式容器在使用方式上基本类似，但是底层实现的数据结构不同。在本篇文章中，我们主要对unordered_map和unordered_set进行介绍。

2.1、 unordered_map

2.1.1、unordered_map的文档介绍

unordered_map的在线文档说明
要点：

unordered_map是存储<key, value>键值对的关联式容器，其允许通过keys快速的索引到与
其对应的value。
在unordered_map中，键值通常用于唯一地标识元素，而映射值是一个对象，其内容与此
键关联。键和映射值的类型可能不同。
在内部,unordered_map没有对<kye, value>按照任何特定的顺序排序, 为了能在常数范围内
找到key所对应的value，unordered_map将相同哈希值的键值对放在相同的桶中。
unordered_map容器通过key访问单个元素要比map快，但它通常在遍历元素子集的范围迭
代方面效率较低。
unordered_maps实现了直接访问操作符(operator[])，它允许使用key作为参数直接访问
value。
它的迭代器至少是前向迭代器。

2.1.2、unordered_map的接口说明

unordered_map的构造

函数声明	功能介绍
unordered_map	构造不同格式的unordered_map对象

unordered_map的容量

函数声明	功能介绍
bool empty() const	检测unordered_map是否为空
size_t size() const	获取unordered_map的有效元素个数

unordered_map的迭代器

函数声明	功能介绍
begin	返回unordered_map第一个元素的迭代器
end	返回unordered_map最后一个元素下一个位置的迭代器
cbegin	返回unordered_map第一个元素的const迭代器
cend	返回unordered_map最后一个元素下一个位置的const迭代器

unordered_map的元素访问

函数声明	功能介绍
operator[]	返回与key对应的value，没有一个默认值

注意：该函数中实际调用哈希桶的插入操作，用参数key与V()构造一个默认值往底层哈希桶中插入，如果key不在哈希桶中，插入成功，返回V()，插入失败，说明key已经在哈希桶中，将key对应的value返回。

unordered_map的查询

函数声明	功能介绍
iterator find(const K& key)	返回key在哈希桶中的位置
size_t count(const K& key)	返回哈希桶中关键码为key的键值对的个数

注意：unordered_map中key是不能重复的，因此count函数的返回值最大为1。

unordered_map的修改操作

函数声明	功能介绍
insert	向容器中插入键值对
erase	删除容器中的键值对
void clear()	清空容器中有效元素个数
void swap(unordered_map&)	交换两个容器中的元素

unordered_map的桶操作

函数声明	功能介绍
size_t bucket_count()const	返回哈希桶中桶的总个数
size_t bucket_size(size_t n)const	返回n号桶中有效元素的总个数
size_t bucket(const K& key)	返回元素key所在的桶号

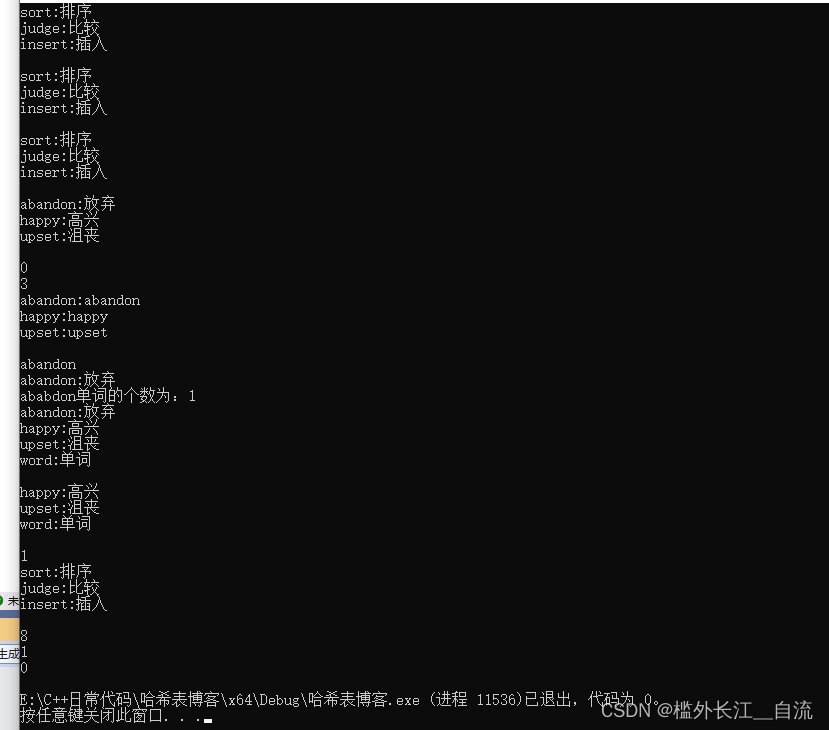
代码演示如下：

#include<iostream>
#include<unordered_map>
#include<string>
using namespace std;

int main()
{
	unordered_map<string, string> mp1;
	mp1["sort"] = "排序";//operator["xxx"]="yyy" :如果xxx存在，插入失败，返回已经存在的yyy,否则插入后再返回yyy
	mp1["judge"] = "比较";
	mp1["insert"] = "插入";
	unordered_map<string, string> mp2(mp1.begin(), mp1.end());
	unordered_map<string, string> mp3 = mp2;
	unordered_map<string, string> mp4 = { {"abandon","放弃"},{"happy","高兴"},{"upset","沮丧"} };
	for (auto& e : mp1)
	{
		cout << e.first << ":" << e.second << endl;
	}
	cout << endl;
	for (auto& e : mp2)
	{
		cout << e.first << ":" << e.second << endl;
	}
	cout << endl;
	for (auto& e : mp3)
	{
		cout << e.first << ":" << e.second << endl;
	}
	cout << endl;
	for (auto& e : mp4)
	{
		cout << e.first << ":" << e.second << endl;
	}
	cout << endl;

	cout << mp1.empty() << endl;//bool empty() const
	cout << mp4.size() << endl; //获取unordered_map的有效元素个数
	auto it = mp4.begin();//begin()
	while (it != mp4.end())//end()
	{
		cout << it->first << ":" << it->first << endl;
		++it;
	}
	cout << endl;
	string input;
	getline(cin, input);
	auto fit = mp4.find(input);
	if (fit != mp4.end())
	{
		cout << fit->first << ":" << fit->second << endl;
	}
	cout << "ababdon单词的个数为：" << mp4.count("abandon") << endl;
	mp4.insert({ "word","单词" });
	for (auto& e : mp4)
	{
		cout << e.first << ":" << e.second << endl;
	}
	cout << endl;
	mp4.erase("abandon");
	for (auto& e : mp4)
	{
		cout << e.first << ":" << e.second << endl;
	}
	cout << endl;

	mp4.clear();
	cout << mp4.empty() << endl;
	mp4.swap(mp1);
	for (auto& e : mp4)
	{
		cout << e.first << ":" << e.second << endl;
	}
	cout << endl;
	cout << mp4.bucket_count() << endl;
	cout << mp4.bucket_size(1) << endl;
	cout << mp4.bucket("insert") << endl;

	return 0;
}

在这里插入图片描述

2.2、 unordered_set

参见 unordered_set在线文档说明

3. 底层结构

unordered系列的关联式容器之所以效率比较高，是因为其底层使用了哈希结构。哈希表是一种使用哈希函数将键（key）映射到桶（bucket）中的数据结构。这个映射过程可以在常数时间内完成，因此哈希表提供了非常快速的插入、删除和查找操作。

3.1 哈希概念

顺序结构以及平衡树中，元素关键码与其存储位置之间没有对应的关系，因此在查找一个元素
时，必须要经过关键码的多次比较。顺序查找时间复杂度为O(N)，平衡树中为树的高度，即
O( $log_2 N$ )，搜索的效率取决于搜索过程中元素的比较次数。
理想的搜索方法：可以不经过任何比较，一次直接从表中得到要搜索的元素。如果构造一种存储结构，通过某种函数(hashFunc)使元素的存储位置与它的关键码之间能够建立一一映射的关系，那么在查找时通过该函数可以很快找到该元素。
当向该结构中：
插入元素：
根据待插入元素的关键码，以此函数计算出该元素的存储位置并按此位置进行存放。

搜索元素：
对元素的关键码进行同样的计算，把求得的函数值当做元素的存储位置，在结构中按此位置
取元素比较，若关键码相等，则搜索成功。
该方式即为哈希(散列)方法，哈希方法中使用的转换函数称为哈希(散列)函数，构造出来的结构称
为哈希表(Hash Table)(或者称散列表)。
例如：数据集合{1，7，6，4，5，9}；
哈希函数设置为：hash(key) = key % capacity; capacity为存储元素底层空间总的大小。
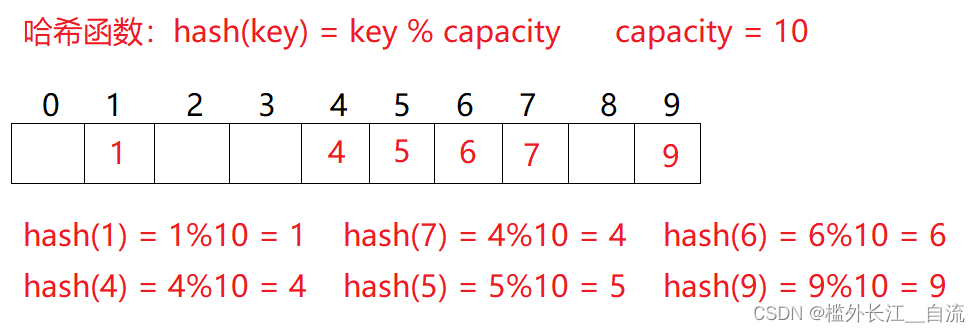
在这里插入图片描述
用该方法进行搜索不必进行多次关键码的比较，因此搜索的速度比较快。
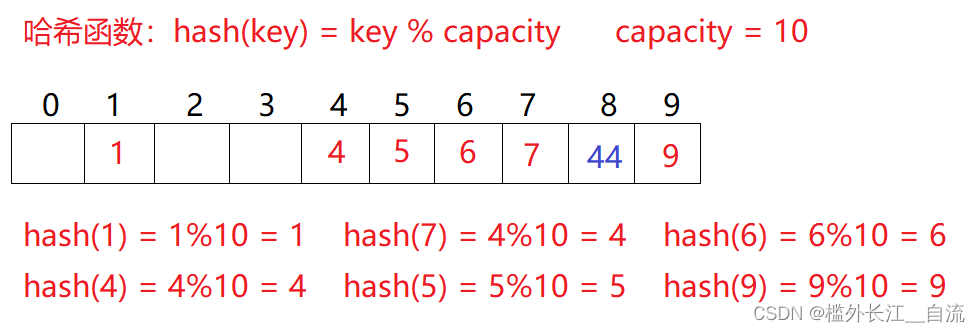
问题：按照上述哈希方式，向集合中插入元素44，会出现什么问题？那么就得说明一下不同元素映射到相同的位置是，产生哈希冲突。

3.2 哈希冲突

对于两个数据元素的关键字 $k_i$ 和 $k_j$ (i != j)，有 $k_i$ != $k_j$ ，但有：Hash( $k_i$ ) ==
Hash( $k_j$ )，即：不同关键字通过相同哈希哈数计算出相同的哈希地址，该种现象称为哈希冲突
或哈希碰撞。
把具有不同关键码而具有相同哈希地址的数据元素称为“同义词”。
发生哈希冲突该如何处理呢？

2.3 哈希函数

引起哈希冲突的一个原因可能是：哈希函数设计不够合理。
哈希函数设计原则：

1、哈希函数的定义域必须包括需要存储的全部关键码，而如果散
列表允许有m个地址时，其值域必须在0到m-1之间
2、哈希函数计算出来的地址能均匀分布在整个空间中
3、哈希函数应该比较简单

常见哈希函数：

直接定址法–(常用)
取关键字的某个线性函数为散列地址：Hash（Key）= A*Key + B
优点：简单、均匀
缺点：需要事先知道关键字的分布情况
使用场景：适合查找比较小且连续的情况
除留余数法–(常用)
设散列表中允许的地址数为m，取一个不大于m，但最接近或者等于m的质数p作为除数，
按照哈希函数：Hash(key) = key% p(p<=m),将关键码转换成哈希地址
平方取中法–(了解)
假设关键字为1234，对它平方就是1522756，抽取中间的3位227作为哈希地址；
再比如关键字为4321，对它平方就是18671041，抽取中间的3位671(或710)作为哈希地址
平方取中法比较适合：不知道关键字的分布，而位数又不是很大的情况。
折叠法–(了解)
折叠法是将关键字从左到右分割成位数相等的几部分(最后一部分位数可以短些)，然后将这
几部分叠加求和，并按散列表表长，取后几位作为散列地址。
折叠法适合事先不需要知道关键字的分布，适合关键字位数比较多的情况。
随机数法–(了解)
选择一个随机函数，取关键字的随机函数值为它的哈希地址，即H(key) = random(key),其中
random为随机数函数。
通常应用于关键字长度不等时采用此法。
数学分析法–(了解)
设有n个d位数，每一位可能有r种不同的符号，这r种不同的符号在各位上出现的频率不一定
相同，可能在某些位上分布比较均匀，每种符号出现的机会均等，在某些位上分布不均匀只
有某几种符号经常出现。可根据散列表的大小，选择其中各种符号分布均匀的若干位作为散
列地址。例如：

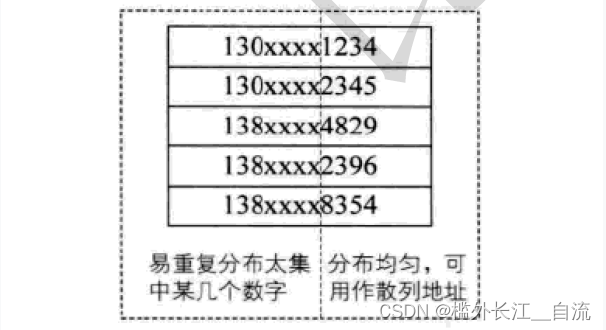
假设要存储某家公司员工登记表，如果用手机号作为关键字，那么极有可能前7位都是相同的，那么我们可以选择后面的四位作为散列地址，如果这样的抽取工作还容易出现冲突，还可以对抽取出来的数字进行反转(如1234改成4321)、右环位移(如1234改成4123)、左环移位、前两数与后两数叠加(如1234改成12+34=46)等方法。
数字分析法通常适合处理关键字位数比较大的情况，如果事先知道关键字的分布且关键字的若干位分布较均匀的情况。
注意：哈希函数设计的越精妙，产生哈希冲突的可能性就越低，但是无法避免哈希冲突。

2.4 哈希冲突解决

解决哈希冲突两种常见的方法是：闭散列和开散列

2.4.1 闭散列

闭散列：也叫开放定址法，当发生哈希冲突时，如果哈希表未被装满，说明在哈希表中必然还有空位置，那么可以把key存放到冲突位置中的“下一个” 空位置中去。那如何寻找下一个空位置呢？
1. 线性探测
比如3.1中的场景，现在需要插入元素44，先通过哈希函数计算哈希地址，hashAddr为4，因此44理论上应该插在该位置，但是该位置已经放了值为4的元素，即发生哈希冲突。
线性探测：从发生冲突的位置开始，依次向后探测，直到寻找到下一个空位置为止。
插入
通过哈希函数获取待插入元素在哈希表中的位置，如果该位置中没有元素则直接插入新元素，如果该位置中有元素发生哈希冲突，使用线性探测找到下一个空位置，插入新元素。
在这里插入图片描述
删除
采用闭散列处理哈希冲突时，不能随便物理删除哈希表中已有的元素，若直接删除元素会影响其他元素的搜索。比如删除元素4，如果直接删除掉，44查找起来可能会受影响。因此线性探测采用标记的伪删除法来删除一个元素。
方法：哈希表每个空间给个标记，EMPTY此位置空， EXIST此位置已经有元素，DELETE元素已经删除。

enum State{EMPTY, EXIST, DELETE};

2.线性探测的实现

// 注意：假如实现的哈希表中元素唯一，即key相同的元素不再进行插入
// 为了实现简单，此哈希表中我们将比较直接与元素绑定在一起
template<class K, class V>
class HashTable
{
  struct Elem
 { 
    pair<K, V> _val;
    State _state;
 };
 
public:
  HashTable(size_t capacity = 3)
   : _ht(capacity), _size(0)
 {
    for(size_t i = 0; i < capacity; ++i)
      _ht[i]._state = EMPTY;
 }
 
 bool Insert(const pair<K, V>& val)
 {
   // 检测哈希表底层空间是否充足
   // _CheckCapacity();
   size_t hashAddr = HashFunc(key);
   // size_t startAddr = hashAddr;
   while(_ht[hashAddr]._state != EMPTY)
   {
     if(_ht[hashAddr]._state == EXIST && _ht[hashAddr]._val.first
== key)
       return false;
    
     hashAddr++;
     if(hashAddr == _ht.capacity())
       hashAddr = 0;
     /*
     // 转一圈也没有找到，注意：动态哈希表，该种情况可以不用考虑，哈希表中元
素个数到达一定的数量，哈希冲突概率会增大，需要扩容来降低哈希冲突，因此哈希表中元素是
不会存满的
     if(hashAddr == startAddr)
       return false;
     */
   }
  
   // 插入元素
   _ht[hashAddr]._state = EXIST;
   _ht[hashAddr]._val = val;
   _size++;
   return true;
 }
 int Find(const K& key)
 {
   size_t hashAddr = HashFunc(key);
   while(_ht[hashAddr]._state != EMPTY)
   {
     if(_ht[hashAddr]._state == EXIST && _ht[hashAddr]._val.first
== key)
       return hashAddr;
    
     hashAddr++;
   }
   return hashAddr;
 }
 bool Erase(const K& key)
 {
   int index = Find(key);
   if(-1 != index)
   {
     _ht[index]._state = DELETE;
     _size++;
     return true;
   }
   return false;
 }
 size_t Size()const;
 bool Empty() const;  
 void Swap(HashTable<K, V, HF>& ht);
private:
  size_t HashFunc(const K& key)
 {
    return key % _ht.capacity();
 }
private:
  vector<Elem> _ht;
  size_t _size;
};

哈希表什么情况下进行扩容？如何扩容？
在这里插入图片描述

void CheckCapacity()
{
  if(_size * 10 / _ht.capacity() >= 7)
 {
    HashTable<K, V, HF> newHt(GetNextPrime(ht.capacity));
    for(size_t i = 0; i < _ht.capacity(); ++i)
   {
      if(_ht[i]._state == EXIST)
        newHt.Insert(_ht[i]._val);
   }
   
    Swap(newHt);
 }
}

线性探测优点：实现非常简单，
线性探测缺点：一旦发生哈希冲突，所有的冲突连在一起，容易产生数据“堆积”，即：不同
关键码占据了可利用的空位置，使得寻找某关键码的位置需要许多次比较，导致搜索效率降
低。如何缓解呢？
二次探测
线性探测的缺陷是产生冲突的数据堆积在一块，这与其找下一个空位置有关系，因为找空位
置的方式就是挨着往后逐个去找，因此二次探测为了避免该问题，找下一个空位置的方法
为： $H_i$ = ( $H_0$ + $i^2$ )% m, 或者： $H_i$ = ( $H_0$ - $i^2$ )% m。其中：i =
1,2,3…， $H_0$ 是通过散列函数Hash(x)对元素的关键码 key 进行计算得到的位置，m是表
的大小。
研究表明：当表的长度为质数且表装载因子a不超过0.5时，新的表项一定能够插入，而且任
何一个位置都不会被探查两次。因此只要表中有一半的空位置，就不会存在表满的问题。在
搜索时可以不考虑表装满的情况，但在插入时必须确保表的装载因子a不超过0.5，如果超出
必须考虑增容。
因此：闭散列最大的缺陷就是空间利用率比较低，这也是哈希的缺陷。

2.4.2 开散列

开散列概念
开散列法又叫链地址法(开链法)，首先对关键码集合用散列函数计算散列地址，具有相同地址的关键码归于同一子集合，每一个子集合称为一个桶，各个桶中的元素通过一个单链表链接起来，各链表的头结点存储在哈希表中。

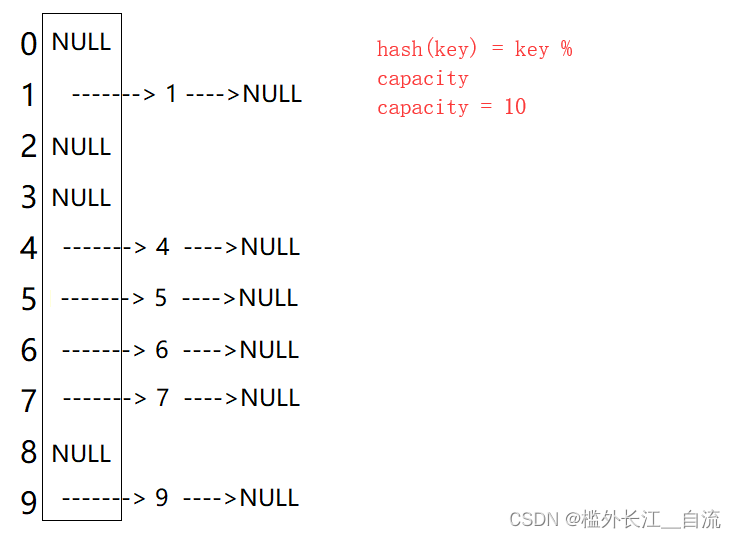
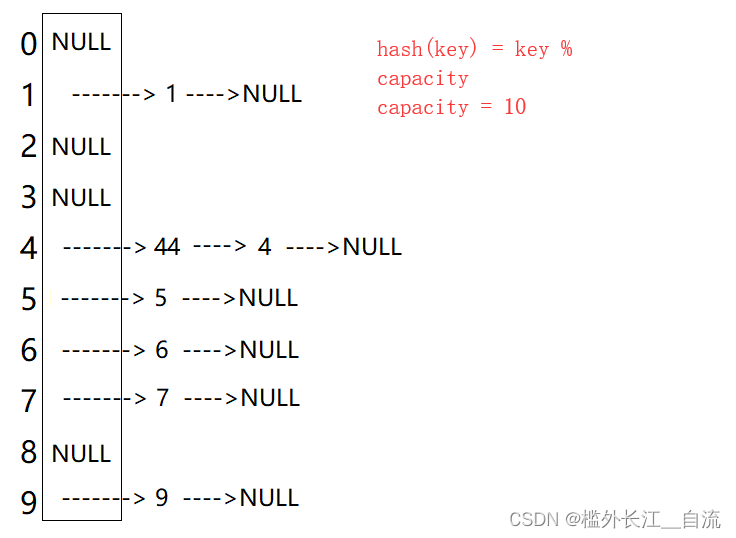
从上图可以看出，开散列中每个桶中放的都是发生哈希冲突的元素。
2. 开散列实现

template<class V>
struct HashBucketNode
{
  HashBucketNode(const V& data)
   : _pNext(nullptr), _data(data)
 {}
  HashBucketNode<V>* _pNext;
  V _data;
};
// 本文所实现的哈希桶中key是唯一的
template<class V>
class HashBucket
{
  typedef HashBucketNode<V> Node;
  typedef Node* PNode;
public:
  HashBucket(size_t capacity = 3): _size(0)
 { _ht.resize(GetNextPrime(capacity), nullptr);}
 
  // 哈希桶中的元素不能重复
  PNode* Insert(const V& data)
 {
    // 确认是否需要扩容。。。
    // _CheckCapacity();
   
    // 1. 计算元素所在的桶号
    size_t bucketNo = HashFunc(data);
   
    // 2. 检测该元素是否在桶中
    PNode pCur = _ht[bucketNo];
    while(pCur)
   {
      if(pCur->_data == data)
        return pCur;
     
      pCur = pCur->_pNext;
   }
   
    // 3. 插入新元素
    pCur = new Node(data);
    pCur->_pNext = _ht[bucketNo];
    _ht[bucketNo] = pCur;
    _size++;
    return pCur;
 }
 
  // 删除哈希桶中为data的元素(data不会重复)，返回删除元素的下一个节点
  PNode* Erase(const V& data)
 {
    size_t bucketNo = HashFunc(data);
    PNode pCur = _ht[bucketNo];
    PNode pPrev = nullptr, pRet = nullptr;
   
    while(pCur)
   {
      if(pCur->_data == data)
     {
        if(pCur == _ht[bucketNo])
          _ht[bucketNo] = pCur->_pNext;
        else
          pPrev->_pNext = pCur->_pNext;
       
        pRet = pCur->_pNext;
        delete pCur;
        _size--;
        return pRet;
     }
   }
   
    return nullptr;
 }
 
  PNode* Find(const V& data);
  size_t Size()const;
  bool Empty()const;
  void Clear();
  bool BucketCount()const;
  void Swap(HashBucket<V, HF>& ht;
  ~HashBucket();
private:
  size_t HashFunc(const V& data)
  {
    return data%_ht.capacity();
 }
private:
  vector<PNode*> _ht;
  size_t _size;    // 哈希表中有效元素的个数
}；

3. 开散列增容
桶的个数是一定的，随着元素的不断插入，每个桶中元素的个数不断增多，极端情况下，可
能会导致一个桶中链表节点非常多，会影响的哈希表的性能，因此在一定条件下需要对哈希
表进行增容，那该条件怎么确认呢？开散列最好的情况是：每个哈希桶中刚好挂一个节点，
再继续插入元素时，每一次都会发生哈希冲突，因此，在元素个数刚好等于桶的个数时，可
以给哈希表增容。

void _CheckCapacity()
{
  size_t bucketCount = BucketCount();
  if(_size == bucketCount)
 {
    HashBucket<V, HF> newHt(bucketCount);
    for(size_t bucketIdx = 0; bucketIdx < bucketCount; ++bucketIdx)
   {
      PNode pCur = _ht[bucketIdx];
      while(pCur)
     {
        // 将该节点从原哈希表中拆出来
        _ht[bucketIdx] = pCur->_pNext;
       
        // 将该节点插入到新哈希表中
        size_t bucketNo = newHt.HashFunc(pCur->_data);
        pCur->_pNext = newHt._ht[bucketNo];
        newHt._ht[bucketNo] = pCur;
        pCur = _ht[bucketIdx];
     }
   }
   
    newHt._size = _size;
    this->Swap(newHt);
 }
}

开散列的思考
只能存储key为整形的元素，其他类型怎么解决？

// 哈希函数采用处理余数法，被模的key必须要为整形才可以处理，此处提供将key转化为
整形的方法
// 整形数据不需要转化
template<class T>
class DefHashF
{
public:
  size_t operator()(const T& val)
 {
    return val;
    }
};
// key为字符串类型，需要将其转化为整形
class Str2Int
{
public:
  size_t operator()(const string& s)
 {
    const char* str = s.c_str();
    unsigned int seed = 131; // 31 131 1313 13131 131313
    unsigned int hash = 0;
    while (*str)
   {
      hash = hash * seed + (*str++);
   }
   
    return (hash & 0x7FFFFFFF);
 }
};
// 为了实现简单，此哈希表中我们将比较直接与元素绑定在一起
template<class V, class HF>
class HashBucket
{
  // ……
private:
  size_t HashFunc(const V& data)
 {
    return HF()(data.first)%_ht.capacity();
 }
};

除留余数法，最好模一个素数，如何每次快速取一个类似两倍关系的素数？

size_t GetNextPrime(size_t prime)
{
	const int PRIMECOUNT = 28;
	static const size_t primeList[PRIMECOUNT] =
	{
		53ul, 97ul, 193ul, 389ul, 769ul,
		1543ul, 3079ul, 6151ul, 12289ul, 24593ul,
		49157ul, 98317ul, 196613ul, 393241ul, 786433ul,
		1572869ul, 3145739ul, 6291469ul, 12582917ul,
		25165843ul,
		50331653ul, 100663319ul, 201326611ul, 402653189ul,
		805306457ul,
		1610612741ul, 3221225473ul, 4294967291ul
	};
		size_t i = 0;
		for (; i < PRIMECOUNT; ++i)
		{
			if (primeList[i] > prime)
			return primeList[i];
		}
	return primeList[i];
}

常见的：字符串哈希算法
5. 开散列与闭散列比较
应用链地址法处理溢出，需要增设链接指针，似乎增加了存储开销。事实上：由于开地址法必须保持大量的空闲空间以确保搜索效率，如二次探查法要求装载因子a <=0.7，而表项所占空间又比指针大的多，所以使用链地址法反而比开地址法节省存储空间。

4. 模拟实现

4.1 哈希表的改造

模板参数列表的改造

// K:关键码类型
// V: 不同容器V的类型不同，如果是unordered_map，V代表一个键值对，如果是
unordered_set,V 为 K
// KeyOfValue: 因为V的类型不同，通过value取key的方式就不同，详细见
unordered_map/set的实现
// HF: 哈希函数仿函数对象类型，哈希函数使用除留余数法，需要将Key转换为整形数字才能
取模
template<class K, class V, class KeyOfValue, class HF = DefHashF<T> >
class HashBucket;

增加迭代器操作

// 为了实现简单，在哈希桶的迭代器类中需要用到hashBucket本身，
template<class K, class V, class KeyOfValue, class HF>
class HashBucket;
// 注意：因为哈希桶在底层是单链表结构，所以哈希桶的迭代器不需要--操作
template <class K, class V, class KeyOfValue, class HF>
struct HBIterator
{
	typedef HashBucket<K, V, KeyOfValue, HF> HashBucket;
	typedef HashBucketNode<V>* PNode;
	typedef HBIterator<K, V, KeyOfValue, HF> Self;
	HBIterator(PNode pNode = nullptr, HashBucket* pHt = nullptr);
	Self& operator++()
	{
	    // 当前迭代器所指节点后还有节点时直接取其下一个节点
		if (_pNode->_pNext)
		_pNode = _pNode->_pNext;
		else
		{
			// 找下一个不空的桶，返回该桶中第一个节点
			size_t bucketNo = _pHt->HashFunc(KeyOfValue()(_pNode-
			>_data))+1;
			for (; bucketNo < _pHt->BucketCount(); ++bucketNo)
			{
				if (_pNode = _pHt->_ht[bucketNo])
				break;
			}
		}
		return *this;
	}
	Self operator++(int);
	  V& operator*();
	V* operator->();
	bool operator==(const Self& it) const;
	bool operator!=(const Self& it) const;
	PNode _pNode;       // 当前迭代器关联的节点
	HashBucket* _pHt;     // 哈希桶--主要是为了找下一个空桶时候方便
	};

增加通过key获取value操作

template<class K, class V, class KeyOfValue, class HF = DefHashF<T> >
class HashBucket
{
friend HBIterator<K, V, KeyOfValue, HF>;
  // ......
public:
typedef HBIterator<K, V, KeyOfValue, HF> Iterator;
//
  // ...
// 迭代器
Iterator Begin()
{
size_t bucketNo = 0;
for (; bucketNo < _ht.capacity(); ++bucketNo)
{
if (_ht[bucketNo])
break;
}
if (bucketNo < _ht.capacity())
return Iterator(_ht[bucketNo], this);
else
return Iterator(nullptr, this);
}
Iterator End(){ return Iterator(nullptr, this);}
  Iterator Find(const K& key);
Iterator Insert(const V& data);
Iterator Erase(const K& key);
 
  // 为key的元素在桶中的个数
size_t Count(const K& key)
{
if(Find(key) != End())
      return 1;
   
    return 0;
}
 
  size_t BucketCount()const{ return _ht.capacity();}
  size_t BucketSize(size_t bucketNo)
 {
    size_t count = 0;
    PNode pCur = _ht[bucketNo];
    while(pCur)
   {
      count++;
      pCur = pCur->_pNext;
   }
   
    return count;
 }
 
  // ......
};

4.2 unordered_map

// unordered_map中存储的是pair<K, V>的键值对，K为key的类型，V为value的类型，HF哈希
函数类型
// unordered_map在实现时，只需将hashbucket中的接口重新封装即可
template<class K, class V, class HF = DefHashF<K>>
class unordered_map
{
	typedef pair<K, V> ValueType;
	typedef HashBucket<K, ValueType, KeyOfValue, HF> HT;
	// 通过key获取value的操作
	struct KeyOfValue
	{
	const K& operator()(const ValueType& data)
	{ return data.first;}
	};
	public:
	typename typedef HT::Iterator iterator;
	public:
	unordered_map(): _ht()
	{}
	
	iterator begin(){ return _ht.Begin();}
	iterator end(){ return _ht.End();}
	
	// capacity
	size_t size()const{ return _ht.Size();}
	bool empty()const{return _ht.Empty();}
	///
	// Acess
	V& operator[](const K& key)
	{
	return (*(_ht.InsertUnique(ValueType(key, V())).first)).second;
	}
	const V& operator[](const K& key)const;
	//
	// lookup
	iterator find(const K& key){ return _ht.Find(key);}
	size_t count(const K& key){ return _ht.Count(key);}
	/
	// modify
	pair<iterator, bool> insert(const ValueType& valye)
	{ return _ht.Insert(valye);}
	iterator erase(iterator position)
	{ return _ht.Erase(position);}
	
	// bucket
	size_t bucket_count(){ return _ht.BucketCount();}
	size_t bucket_size(const K& key){ return _ht.BucketSize(key);}
	private:
	HT _ht;
};

5、哈希的应用

5.1 位图

5.1.1 位图概念

面试题
给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在
这40亿个数中。【腾讯】
遍历，时间复杂度O(N)
排序(O(NlogN))，利用二分查找: logN
位图解决
数据是否在给定的整形数据中，结果是在或者不在，刚好是两种状态，那么可以使用一
个二进制比特位来代表数据是否存在的信息，如果二进制比特位为1，代表存在，为0
代表不存在。比如：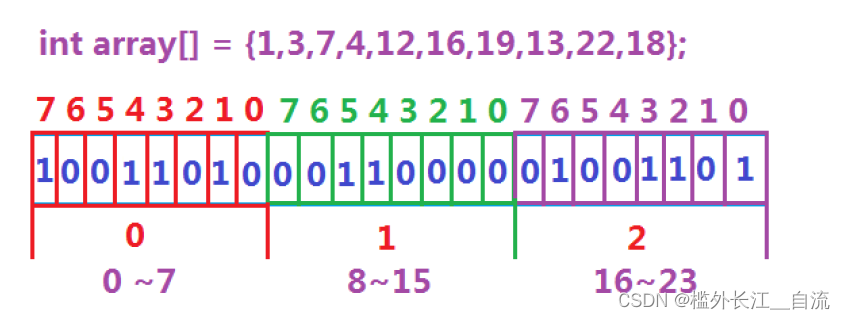
位图概念
所谓位图，就是用每一位来存放某种状态，适用于海量数据，数据无重复的场景。通常是用
来判断某个数据存不存在的。

5.1.2 位图的实现

class bitset
{
public:
	bitset(size_t bitCount)
	: _bit((bitCount>>5)+1), _bitCount(bitCount)
	{}
	// 将which比特位置1
	void set(size_t which)
	{
	if(which > _bitCount)
	return;
	size_t index = (which >> 5);
	size_t pos = which % 32;
	_bit[index] |= (1 << pos);
	}
	// 将which比特位置0
	void reset(size_t which)
	{
	if(which > _bitCount)
	return;
	size_t index = (which >> 5);
	size_t pos = which % 32;
	_bit[index] &= ~(1<<pos);
	}
	// 检测位图中which是否为1
	bool test(size_t which)
	{
	if(which > _bitCount)
	return false;
	size_t index = (which >> 5);
	size_t pos = which % 32;
	return _bit[index] & (1<<pos);
	}
	// 获取位图中比特位的总个数
	size_t size()const{ return _bitCount;}
	// 位图中比特为1的个数
	size_t Count()const
	{
	  int bitCnttable[256] = {
	0, 1, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, 2, 3, 3, 4, 1, 2, 2, 3, 2, 3, 3, 4, 2,
	3, 3, 4, 3, 4, 4, 5, 1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5, 2, 3,
	3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6, 1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3,
	4, 3, 4, 4, 5, 2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6, 2, 3, 3, 4,
	3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6, 3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5,
	6, 6, 7, 1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5, 2, 3, 3, 4, 3, 4,
	4, 5, 3, 4, 4, 5, 4, 5, 5, 6, 2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5,
	6, 3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7, 2, 3, 3, 4, 3, 4, 4, 5,
	3, 4, 4, 5, 4, 5, 5, 6, 3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7, 3,
	4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7, 4, 5, 5, 6, 5, 6, 6, 7, 5, 6,
	6, 7, 6, 7, 7, 8};
	size_t size = _bit.size();
	size_t count = 0;
	for(size_t i = 0; i < size; ++i)
	{
	int value = _bit[i];
	int j = 0;
	while(j < sizeof(_bit[0]))
	{
	unsigned char c = value;
	count += bitCntTable[c];
	++j;
	value >>= 8;
	}
	}
	return count;
	}
private:
	vector<int> _bit;
	size_t _bitCount;
}

5.1.3 位图的应用

快速查找某个数据是否在一个集合中
排序 + 去重
求两个集合的交集、并集等
操作系统中磁盘块标记

5.2 布隆过滤器

5.2.1 布隆过滤器提出

我们在使用新闻客户端看新闻时，它会给我们不停地推荐新的内容，它每次推荐时要去重，去掉
那些已经看过的内容。问题来了，新闻客户端推荐系统如何实现推送去重的？用服务器记录了用
户看过的所有历史记录，当推荐系统推荐新闻时会从每个用户的历史记录里进行筛选，过滤掉那
些已经存在的记录。如何快速查找呢？

用哈希表存储用户记录，缺点：浪费空间
用位图存储用户记录，缺点：位图一般只能处理整形，如果内容编号是字符串，就无法处理
了。
将哈希与位图结合，即布隆过滤器

5.2.2布隆过滤器概念

布隆过滤器是由布隆（Burton Howard Bloom）在1970年提出的一种紧凑型的、比较巧妙的概率型数据结构，特点是高效地插入和查询，可以用来告诉你 “某样东西一定不存在或者可能存在”，它是用多个哈希函数，将一个数据映射到位图结构中。此种方式不仅可以提升查询效率，也可以节省大量的内存空间。
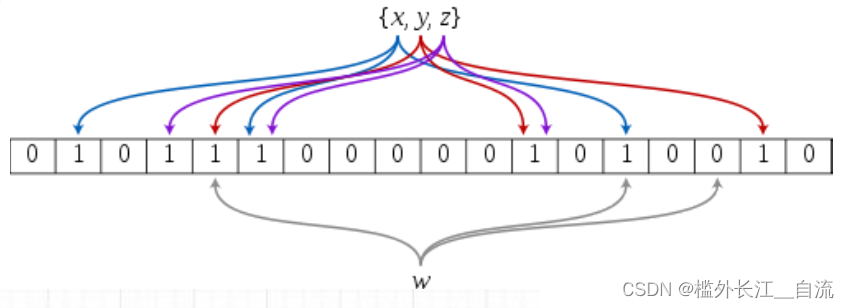
在这里插入图片描述
布隆过滤器讲解

5.2.3 布隆过滤器的插入

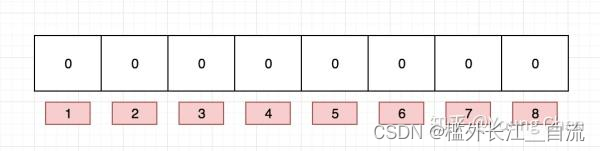
在这里插入图片描述
向布隆过滤器中插入：“baidu”

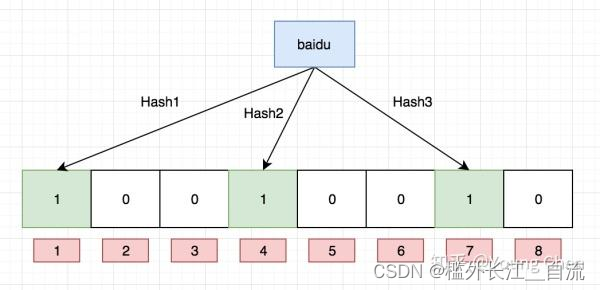
struct BKDRHash
{
	size_t operator()(const string& s)
	{
		// BKDR
		size_t value = 0;
		for (auto ch : s)
		{
			value *= 31;
			value += ch;
		}
		return value;
	}
};
struct APHash
{
	size_t operator()(const string& s)
	{
		size_t hash = 0;
		for (long i = 0; i < s.size(); i++)
		{
			if ((i & 1) == 0)
		{
			hash ^= ((hash << 7) ^ s[i] ^ (hash >> 3));
		}
		else
		{
			hash ^= (~((hash << 11) ^ s[i] ^ (hash >> 5)));
		}
		}
		return hash;
	}
};
struct DJBHash
{
	size_t operator()(const string& s)
	{
		size_t hash = 5381;
		for (auto ch : s)
		{
			hash += (hash << 5) + ch;
		}
		return hash;
	}
};
template<size_t N,
size_t X = 5,
class K = string,
class HashFunc1 = BKDRHash,
class HashFunc2 = APHash,
class HashFunc3 = DJBHash>
class BloomFilter
{
public:
	void Set(const K& key)
	{
	size_t len = X*N;
	size_t index1 = HashFunc1()(key) % len;
	size_t index2 = HashFunc2()(key) % len;
	size_t index3 = HashFunc3()(key) % len;
	/* cout << index1 << endl;
	cout << index2 << endl;
	cout << index3 << endl<<endl;*/
	_bs.set(index1);
	_bs.set(index2);
	_bs.set(index3);
	}
	bool Test(const K& key)
	{
		size_t len = X*N;
		size_t index1 = HashFunc1()(key) % len;
		if (_bs.test(index1) == false)
			return false;
		size_t index2 = HashFunc2()(key) % len;
		if (_bs.test(index2) == false)
			return false;
		size_t index3 = HashFunc3()(key) % len;
		if (_bs.test(index3) == false)
			return false;
		return true;  // 存在误判的
	}
	// 不支持删除，删除可能会影响其他值。
	void Reset(const K& key);
private:
	bitset<X*N> _bs;
};

5.2.4 布隆过滤器的查找

布隆过滤器的思想是将一个元素用多个哈希函数映射到一个位图中，因此被映射到的位置的比特位一定为1。所以可以按照以下方式进行查找：分别计算每个哈希值对应的比特位置存储的是否为零，只要有一个为零，代表该元素一定不在哈希表中，否则可能在哈希表中。注意：布隆过滤器如果说某个元素不存在时，该元素一定不存在，如果该元素存在时，该元素可能存在，因为有些哈希函数存在一定的误判。比如：在布隆过滤器中查找"alibaba"时，假设3个哈希函数计算的哈希值为：1、3、7，刚好和其他元素的比特位重叠，此时布隆过滤器告诉该元素存在，但实该元素是不存在的。

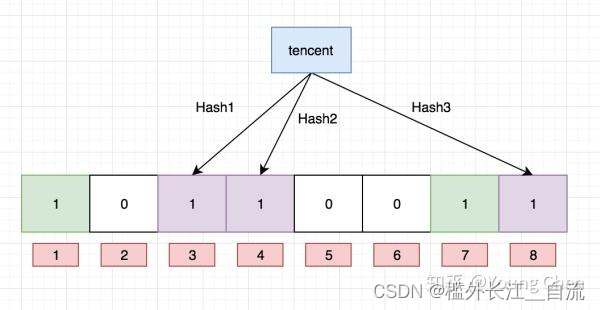
5.2.5 布隆过滤器删除

布隆过滤器不能直接支持删除工作，因为在删除一个元素时，可能会影响其他元素。
比如：删除上图中"tencent"元素，如果直接将该元素所对应的二进制比特位置0，“baidu”元素也
被删除了，因为这两个元素在多个哈希函数计算出的比特位上刚好有重叠。
一种支持删除的方法：将布隆过滤器中的每个比特位扩展成一个小的计数器，插入元素时给k个计
数器(k个哈希函数计算出的哈希地址)加一，删除元素时，给k个计数器减一，通过多占用几倍存储
空间的代价来增加删除操作。
缺陷：