pyro库应用第 1 部分----贝叶斯回归

Bayesian Regression - Introduction (Part 1) — Pyro Tutorials 1.8.6 documentation

一、说明

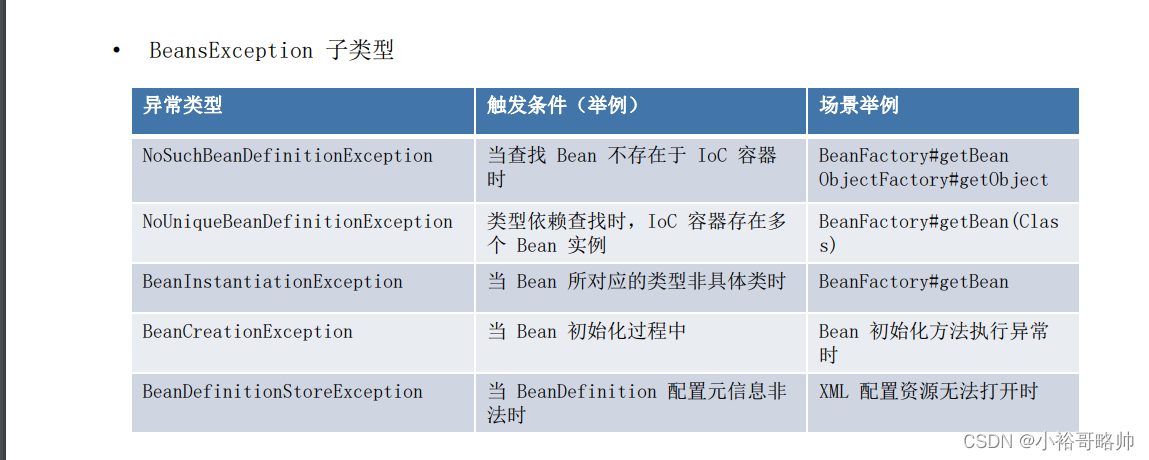
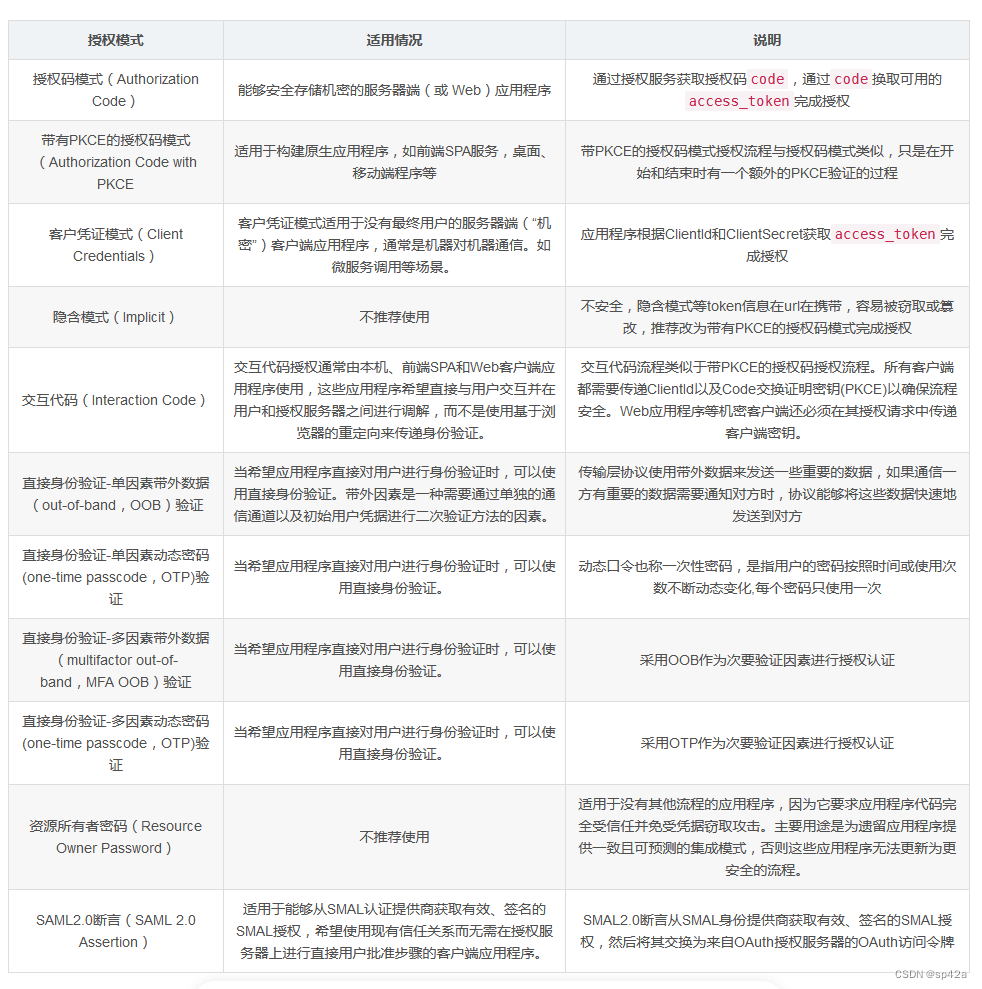
我们很熟悉线性回归的问题，然而，一些问题看似不似线性问题，但是，用贝叶斯回归却可以解决。本文使用土地平整度和国家GDP的关系数据集进行回归分析，发现线性回归无法解决的问题，从贝叶斯回归给出答案。

二、贝叶斯回归简介

回归是机器学习中最常见和基本的监督学习任务之一。假设我们有一个数据集 $\mathcal{D}$ 形式的

$\mathcal{D} = \{ (X_i, y_i) \} \qquad \text{for}\qquad i=1,2,...,N$

线性回归的目标是将函数拟合到以下形式的数据：

$y = w X + b + \epsilon$

在这里w和b是可学习的参数并且 $\epsilon$ 代表观测噪声。具体来说w是一个权重矩阵，并且b是一个偏置向量。

在本教程中，我们将首先在 PyTorch 中实现线性回归并学习参数的点估计w和b。然后我们将了解如何使用 Pyro 实现贝叶斯回归，将不确定性纳入我们的估计中。此外，我们将学习如何使用 Pyro 的实用函数进行预测并使用TorchScript.

三、教程大纲

设置
- 数据集
线性回归
- 使用 PyTorch 优化器进行训练
- 回归拟合
使用 Pyro 的 SVI 进行贝叶斯回归
- 模型
- 使用自动指南
- 优化证据下限
模型评估
使用 TorchScript 为模型提供服务

四、基础设置

4.1 导入模块

让我们首先导入我们需要的模块。

[1]:

%reset -s -f

[2]:

import os
from functools import partial
import torch
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

import pyro
import pyro.distributions as dist

# for CI testing
smoke_test = ('CI' in os.environ)
assert pyro.__version__.startswith('1.8.6')
pyro.set_rng_seed(1)


# Set matplotlib settings
%matplotlib inline
plt.style.use('default')

4.2 导入数据集

以下示例改编自[1]。我们想探讨一个国家的地形异质性（通过地形崎岖指数（数据集中的变量崎岖度）衡量）与其人均 GDP 之间的关系。特别是，[2] 中的作者指出，地形崎岖或恶劣的地理位置与非洲以外地区较差的经济表现有关，但崎岖的地形对非洲国家的收入产生了相反的影响。让我们看一下数据并研究这种关系。我们将重点关注数据集中的三个特征：

rugged：量化地形坚固性指数
cont_africa：指定国家是否在非洲
rgdppc_2000：2000年实际人均GDP

响应变量 GDP 高度偏态，因此我们将对它进行对数变换。

[3]:

DATA_URL = "https://d2hg8soec8ck9v.cloudfront.net/datasets/rugged_data.csv"
data = pd.read_csv(DATA_URL, encoding="ISO-8859-1")
df = data[["cont_africa", "rugged", "rgdppc_2000"]]
df = df[np.isfinite(df.rgdppc_2000)]
df["rgdppc_2000"] = np.log(df["rgdppc_2000"])

[4]:

fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(12, 6), sharey=True)
african_nations = df[df["cont_africa"] == 1]
non_african_nations = df[df["cont_africa"] == 0]
sns.scatterplot(x=non_african_nations["rugged"],y=non_african_nations["rgdppc_2000"], ax=ax[0])
ax[0].set(xlabel="Terrain Ruggedness Index",ylabel="log GDP (2000)",   title="Non African Nations")
sns.scatterplot(x=african_nations["rugged"],y=african_nations["rgdppc_2000"],  ax=ax[1])
ax[1].set(xlabel="Terrain Ruggedness Index", ylabel="log GDP (2000)",  title="African Nations");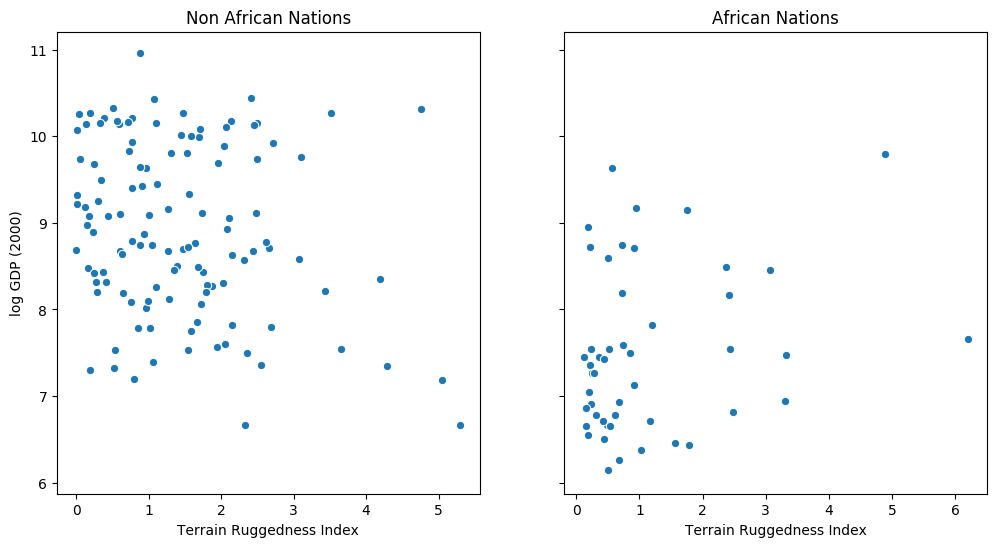

_images/bayesian_regression_6_0.png

4.3 线性回归

我们希望根据数据集中的两个特征来预测一个国家的人均 GDP 对数 - 该国家是否位于非洲及其地形崎岖指数。我们将创建一个简单的类，称为PyroModule和PyroModule[nn.Linear]的子类。与 PyTorch 非常相似，但还支持Pyro 原语作为可以由 Pyro效果处理程序修改的属性（请参阅下一节，了解如何拥有作为原语的模块属性）。一些一般注意事项：torch.nn.LinearPyroModulenn.Modulepyro.sample

PyTorch 模块中的可学习参数是的实例nn.Parameter，在本例中是该类的weight和bias参数nn.Linear。当在 a 中声明PyroModule为属性时，它们会自动注册到 Pyro 的参数存储中。虽然该模型不需要我们在优化过程中约束这些参数的值，但这也可以通过PyroModule使用 PyroParam语句轻松实现。
请注意，虽然的forward方法PyroModule[nn.Linear]继承自nn.Linear，但它也可以很容易地被重写。例如，在逻辑回归的情况下，我们对线性预测器应用 sigmoid 变换。

[5]:

from torch import nn
from pyro.nn import PyroModule

assert issubclass(PyroModule[nn.Linear], nn.Linear)
assert issubclass(PyroModule[nn.Linear], PyroModule)

4.3.1 使用 PyTorch 优化器进行训练

请注意，除了rugged和两个特征cont_africa之外，我们还在模型中包含了一个交互项，它使我们能够分别模拟坚固性对非洲境内和境外国家 GDP 的影响。

我们使用均方误差（MSE）作为损失，使用 Adam 作为模块的优化器torch.optim。我们想要优化模型的参数，即网络的weight和bias参数，它们对应于我们的回归系数和截距。

[6]:

# Dataset: Add a feature to capture the interaction between "cont_africa" and "rugged"
df["cont_africa_x_rugged"] = df["cont_africa"] * df["rugged"]
data = torch.tensor(df[["cont_africa", "rugged", "cont_africa_x_rugged", "rgdppc_2000"]].values,
                        dtype=torch.float)
x_data, y_data = data[:, :-1], data[:, -1]

# Regression model
linear_reg_model = PyroModule[nn.Linear](3, 1)

# Define loss and optimize
loss_fn = torch.nn.MSELoss(reduction='sum')
optim = torch.optim.Adam(linear_reg_model.parameters(), lr=0.05)
num_iterations = 1500 if not smoke_test else 2

def train():
    # run the model forward on the data
    y_pred = linear_reg_model(x_data).squeeze(-1)
    # calculate the mse loss
    loss = loss_fn(y_pred, y_data)
    # initialize gradients to zero
    optim.zero_grad()
    # backpropagate
    loss.backward()
    # take a gradient step
    optim.step()
    return loss

for j in range(num_iterations):
    loss = train()
    if (j + 1) % 50 == 0:
        print("[iteration %04d] loss: %.4f" % (j + 1, loss.item()))


# Inspect learned parameters
print("Learned parameters:")
for name, param in linear_reg_model.named_parameters():
    print(name, param.data.numpy())

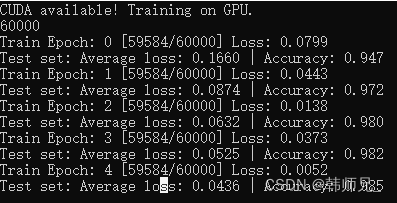
[迭代0050]损失：3179.7852
[迭代0100]损失：1616.1371
[迭代0150]损失：1109.4117
[迭代0200]损失：833.7545
[迭代0250]损失：637.5822
[迭代0300]损失：488.2652
[迭代0350]损失：376.4650
[迭代0400]损失：296.0483
[迭代0450]损失：240.6140
[迭代0500]损失：203.9386
[迭代0550]损失：180.6171
[迭代0600]损失：166.3493
[迭代0650]损失：157.9457
[迭代0700]损失：153.1786
[迭代0750]损失：150.5735
[迭代0800]损失：149.2020
[迭代0850]损失：148.5065
[迭代0900]损失：148.1668
[迭代0950]损失：148.0070
[迭代1000]损失：147.9347
[迭代1050]损失：147.9032
[迭代1100]损失：147.8900
[迭代1150]损失：147.8847
[迭代1200]损失：147.8827
[迭代1250]损失：147.8819
[迭代1300]损失：147.8817
[迭代1350]损失：147.8816
[迭代1400]损失：147.8815
[迭代1450]损失：147.8815
[迭代1500]损失：147.8815
学习到的参数：
重量 [[-1.9478593 -0.20278624 0.39330274]]
偏见[9.22308]

4.3.2 绘制回归拟合图

让我们分别针对非洲以外和非洲内部的国家绘制适合我们模型的回归。

[7]:

fit = df.copy()
fit["mean"] = linear_reg_model(x_data).detach().cpu().numpy()

fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(12, 6), sharey=True)
african_nations = fit[fit["cont_africa"] == 1]
non_african_nations = fit[fit["cont_africa"] == 0]
fig.suptitle("Regression Fit", fontsize=16)
ax[0].plot(non_african_nations["rugged"], non_african_nations["rgdppc_2000"], "o")
ax[0].plot(non_african_nations["rugged"], non_african_nations["mean"], linewidth=2)
ax[0].set(xlabel="Terrain Ruggedness Index",
          ylabel="log GDP (2000)",
          title="Non African Nations")
ax[1].plot(african_nations["rugged"], african_nations["rgdppc_2000"], "o")
ax[1].plot(african_nations["rugged"], african_nations["mean"], linewidth=2)
ax[1].set(xlabel="Terrain Ruggedness Index",
          ylabel="log GDP (2000)",
          title="African Nations");

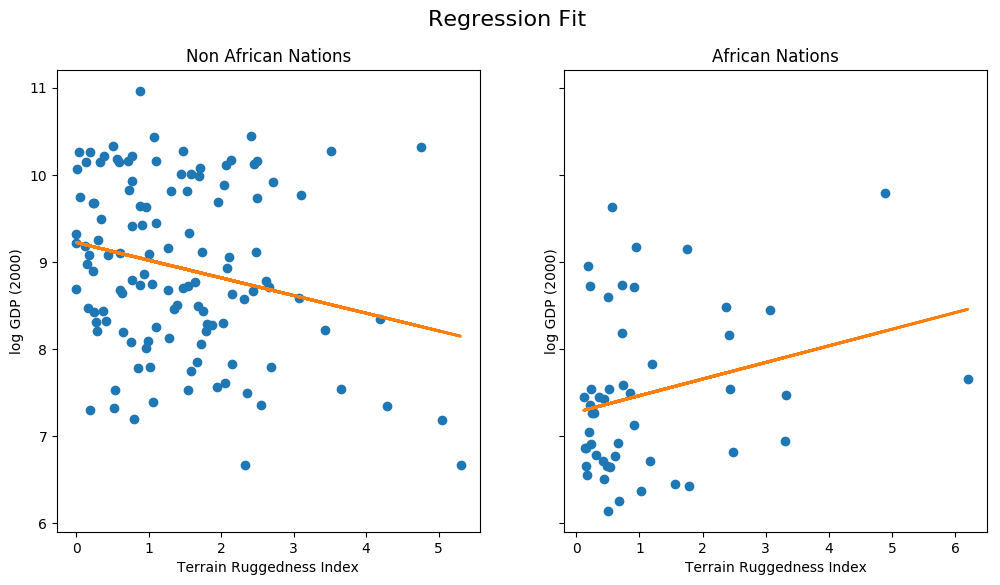
_images/bayesian_regression_12_0.png

我们注意到，地形崎岖程度与非非洲国家的 GDP 呈反比关系，但对非洲国家的 GDP 却有正向影响。然而，目前尚不清楚这种趋势有多强劲。特别是，我们想了解回归拟合如何因参数不确定性而变化。为了解决这个问题，我们将构建一个简单的线性回归贝叶斯模型。贝叶斯建模为推理模型不确定性提供了一个系统框架。我们不仅要学习点估计，还要学习与观察到的数据一致的参数分布。

4.4 使用 Pyro 随机变分推理 (SVI) 的贝叶斯回归

4.4.1 模型

为了使我们的线性回归贝叶斯模型成立，我们需要对参数进行先验�和�。这些分布代表了我们对合理值的先前信念�和�（在观察任何数据之前）。

PyroModule与之前一样，为线性回归创建贝叶斯模型非常直观。请注意以下事项：

该BayesianRegression模块内部使用相同的PyroModule[nn.Linear]模块。但请注意，我们用语句替换了该模块的theweight和 the 。这些语句允许我们对和参数进行先验，而不是将它们视为固定的可学习参数。对于偏差分量，我们设置了一个相当宽的先验，因为它可能远高于 0。biasPyroSampleweightbias
该BayesianRegression.forward方法指定了生成过程。我们通过调用该模块来生成响应的平均值linear（如您所见，该模块从先前的参数中采样weight并bias返回平均响应的值）。最后，我们使用该语句obs的参数来以学习到的观察噪声pyro.sample来调节观察到的数据。该模型返回变量给出的回归线。y_datasigmamean

[8]:

from pyro.nn import PyroSample


class BayesianRegression(PyroModule):
    def __init__(self, in_features, out_features):
        super().__init__()
        self.linear = PyroModule[nn.Linear](in_features, out_features)
        self.linear.weight = PyroSample(dist.Normal(0., 1.).expand([out_features, in_features]).to_event(2))
        self.linear.bias = PyroSample(dist.Normal(0., 10.).expand([out_features]).to_event(1))

    def forward(self, x, y=None):
        sigma = pyro.sample("sigma", dist.Uniform(0., 10.))
        mean = self.linear(x).squeeze(-1)
        with pyro.plate("data", x.shape[0]):
            obs = pyro.sample("obs", dist.Normal(mean, sigma), obs=y)
        return mean

4.4.2 使用自动指南

为了进行推理，即学习未观察到的参数的后验分布，我们将使用随机变分推理（SVI）。该指南确定一个分布族，SVI旨在从该族中找到与真实后验具有最低 KL 散度的近似后验分布。

用户可以在 Pyro 中编写任意灵活的自定义指南，但在本教程中，我们将仅限于 Pyro 的自动指南库。在下一个教程中，我们将探索如何手动编写指南。

首先，我们将使用指南，将AutoDiagonalNormal模型中未观察到的参数的分布建模为具有对角协方差的高斯分布，即假设潜在变量之间不存在相关性（这是一个很强的建模假设，我们将在第 5 部分中看到）二）。在底层，这定义了一个guide使用具有与模型中的Normal每个语句相对应的可学习参数的分布的分布。sample例如，在我们的例子中，该分布的大小应对应(5,)于每个项的 3 个回归系数，并且截距项和sigma模型中各有 1 个分量。

Autoguide 还支持学习 MAP 估计AutoDelta或编写指南AutoGuideList（有关更多信息，请参阅文档）。

[9]:

from pyro.infer.autoguide import AutoDiagonalNormal

model = BayesianRegression(3, 1)
guide = AutoDiagonalNormal(model)

4.4.3 优化证据下限

我们将使用随机变分推理（SVI）（有关 SVI 的介绍，请参阅SVI 第 I 部分）进行推理。就像在非贝叶斯线性回归模型中一样，训练循环的每次迭代都将采取梯度步骤，不同之处在于，在本例中，我们将使用证据下界 (ELBO) 目标，而不是通过构建 MSE 损失Trace_ELBO我们传递给的对象SVI。

[10]:

from pyro.infer import SVI, Trace_ELBO


adam = pyro.optim.Adam({"lr": 0.03})
svi = SVI(model, guide, adam, loss=Trace_ELBO())

请注意，我们使用AdamPyrooptim模块中的优化器，而不是torch.optim之前的模块。这Adam是一个薄薄的包装torch.optim.Adam（请参阅此处进行讨论）。中的优化器pyro.optim用于优化和更新 Pyro 参数存储中的参数值。特别是，您会注意到我们不需要将可学习的参数传递给优化器，因为这是由指导代码确定的，并且在类的幕后SVI自动发生。要采取 ELBO 梯度步骤，我们只需调用 SVI 的步骤方法。我们传递给的 data 参数SVI.step将同时传递给model()和guide()。完整的训练循环如下：

[11]:

pyro.clear_param_store()
for j in range(num_iterations):
    # calculate the loss and take a gradient step
    loss = svi.step(x_data, y_data)
    if j % 100 == 0:
        print("[iteration %04d] loss: %.4f" % (j + 1, loss / len(data)))

[迭代0001]损失：6.2310
[迭代0101]损失：3.5253
[迭代0201]损失：3.2347
[迭代0301]损失：3.0890
[迭代0401]损失：2.6377
[迭代0501]损失：2.0626
[迭代0601]损失：1.4852
[迭代0701]损失：1.4631
[迭代0801]损失：1.4632
[迭代0901]损失：1.4592
[迭代1001]损失：1.4940
[迭代1101]损失：1.4988
[迭代1201]损失：1.4938
[迭代1301]损失：1.4679
[迭代1401]损失：1.4581

我们可以通过从 Pyro 的参数存储中获取来检查优化的参数值。

[12]:

guide.requires_grad_(False)

for name, value in pyro.get_param_store().items():
    print(name, pyro.param(name))

AutoDiagonalNormal.loc 参数包含：
张量([-2.2371, -1.8097, -0.1691, 0.3791, 9.1823])
AutoDiagonalNormal.scale 张量([0.0551, 0.1142, 0.0387, 0.0769, 0.0702])

AutoDiagonalNormal.scale正如您所看到的，我们现在对学习参数进行了不确定性估计 ( )，而不仅仅是点估计。请注意，Autoguide 将潜在变量打包到单个张量中，在本例中，模型中采样的每个变量都有一个条目。正如我们之前所说，loc和scale参数都有 size (5,)，一个对应模型中的每个潜在变量。

为了更清楚地查看潜在参数的分布，我们可以使用AutoDiagonalNormal.quantiles从自动引导中解压潜在样本的方法，并自动将它们约束到站点的支持（例如变量sigma必须位于）。我们看到参数的中值非常接近我们从第一个模型获得的最大似然点估计。(0, 10)

[13]:

guide.quantiles([0.25, 0.5, 0.75])

[13]:

{'西格玛'：[张量（0.9328），张量（0.9647），张量（0.9976）]，
 '线性.权重': [张量([[-1.8868,-0.1952,0.3272]]),
  张量([[-1.8097,-0.1691,0.3791]]),
  张量([[-1.7327,-0.1429,0.4309]])],
 '线性.偏差'：[张量（[9.1350]），张量（[9.1823]），张量（[9.2297]）]}

4.5 模型评估

为了评估我们的模型，我们将生成一些预测样本并查看后验。为此，我们将使用Predictive实用程序类。

我们从经过训练的模型中生成 800 个样本。在内部，这是通过首先为中未观察到的站点生成样本guide，然后通过将站点调整为从中采样的值来向前运行模型来完成的guide。请参阅模型服务部分以深入了解该类的Predictive工作原理。
请注意，在中，我们指定了捕获回归线的模型的return_sites结果（"obs"站点）和返回值（）。"_RETURN"此外，我们还想捕获回归系数（由给出"linear.weight"）以进行进一步分析。
其余代码仅用于绘制模型中两个变量的 90% CI。

[14]:

from pyro.infer import Predictive


def summary(samples):
    site_stats = {}
    for k, v in samples.items():
        site_stats[k] = {
            "mean": torch.mean(v, 0),
            "std": torch.std(v, 0),
            "5%": v.kthvalue(int(len(v) * 0.05), dim=0)[0],
            "95%": v.kthvalue(int(len(v) * 0.95), dim=0)[0],
        }
    return site_stats


predictive = Predictive(model, guide=guide, num_samples=800,
                        return_sites=("linear.weight", "obs", "_RETURN"))
samples = predictive(x_data)
pred_summary = summary(samples)

[15]:

mu = pred_summary["_RETURN"]
y = pred_summary["obs"]
predictions = pd.DataFrame({
    "cont_africa": x_data[:, 0],
    "rugged": x_data[:, 1],
    "mu_mean": mu["mean"],
    "mu_perc_5": mu["5%"],
    "mu_perc_95": mu["95%"],
    "y_mean": y["mean"],
    "y_perc_5": y["5%"],
    "y_perc_95": y["95%"],
    "true_gdp": y_data,
})

[16]:

fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(12, 6), sharey=True)
african_nations = predictions[predictions["cont_africa"] == 1]
non_african_nations = predictions[predictions["cont_africa"] == 0]
african_nations = african_nations.sort_values(by=["rugged"])
non_african_nations = non_african_nations.sort_values(by=["rugged"])
fig.suptitle("Regression line 90% CI", fontsize=16)
ax[0].plot(non_african_nations["rugged"],
           non_african_nations["mu_mean"])
ax[0].fill_between(non_african_nations["rugged"],
                   non_african_nations["mu_perc_5"],
                   non_african_nations["mu_perc_95"],
                   alpha=0.5)
ax[0].plot(non_african_nations["rugged"],
           non_african_nations["true_gdp"],
           "o")
ax[0].set(xlabel="Terrain Ruggedness Index",
          ylabel="log GDP (2000)",
          title="Non African Nations")
idx = np.argsort(african_nations["rugged"])
ax[1].plot(african_nations["rugged"],
           african_nations["mu_mean"])
ax[1].fill_between(african_nations["rugged"],
                   african_nations["mu_perc_5"],
                   african_nations["mu_perc_95"],
                   alpha=0.5)
ax[1].plot(african_nations["rugged"],
           african_nations["true_gdp"],
           "o")
ax[1].set(xlabel="Terrain Ruggedness Index",
          ylabel="log GDP (2000)",
          title="African Nations");

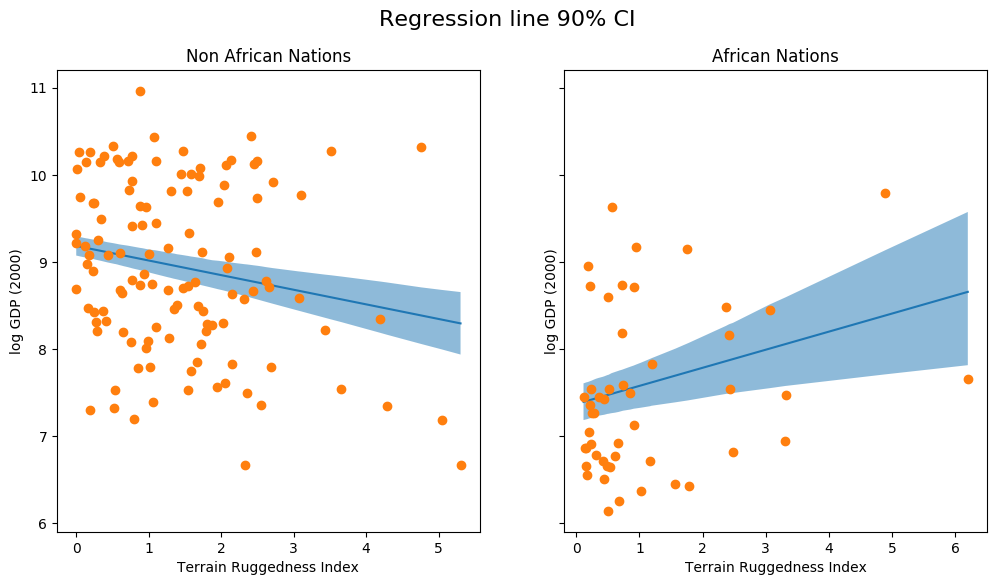
_images/bayesian_regression_29_0.png

上图显示了我们对回归线估计的不确定性，以及均值附近的 90% CI。我们还可以看到，大多数数据点实际上位于 90% CI 之外，这是预料之中的，因为我们没有绘制将受到影响的结果变量sigma！接下来我们就这样做吧。

[17]:

fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(12, 6), sharey=True)
fig.suptitle("Posterior predictive distribution with 90% CI", fontsize=16)
ax[0].plot(non_african_nations["rugged"],
           non_african_nations["y_mean"])
ax[0].fill_between(non_african_nations["rugged"],
                   non_african_nations["y_perc_5"],
                   non_african_nations["y_perc_95"],
                   alpha=0.5)
ax[0].plot(non_african_nations["rugged"],
           non_african_nations["true_gdp"],
           "o")
ax[0].set(xlabel="Terrain Ruggedness Index",
          ylabel="log GDP (2000)",
          title="Non African Nations")
idx = np.argsort(african_nations["rugged"])

ax[1].plot(african_nations["rugged"],
           african_nations["y_mean"])
ax[1].fill_between(african_nations["rugged"],
                   african_nations["y_perc_5"],
                   african_nations["y_perc_95"],
                   alpha=0.5)
ax[1].plot(african_nations["rugged"],
           african_nations["true_gdp"],
           "o")
ax[1].set(xlabel="Terrain Ruggedness Index",
          ylabel="log GDP (2000)",
          title="African Nations");

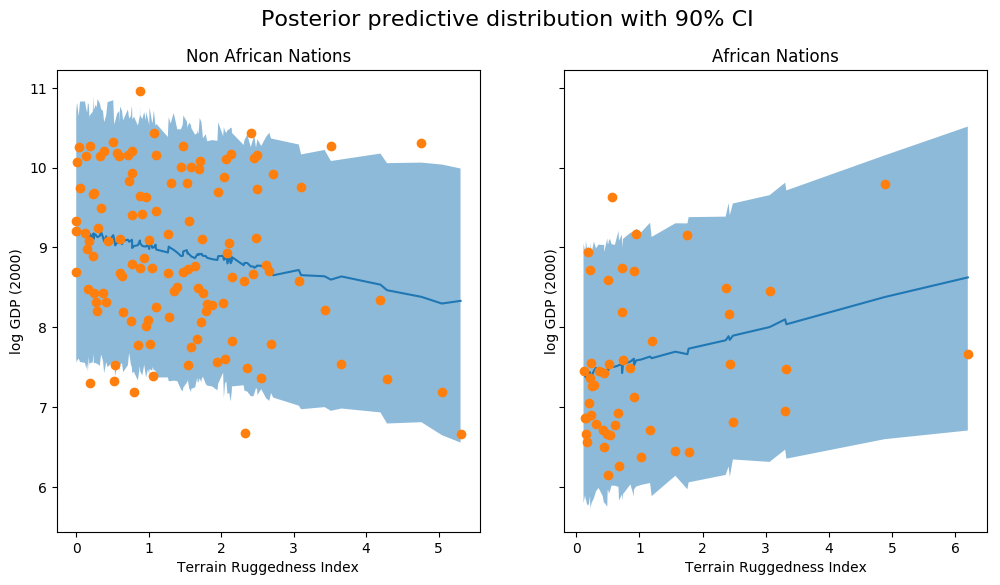
_images/bayesian_regression_31_0.png

我们观察到，我们的模型的结果和 90% CI 占我们在实践中观察到的大部分数据点。进行此类后验预测检查以查看我们的模型是否给出有效的预测通常是一个好主意。

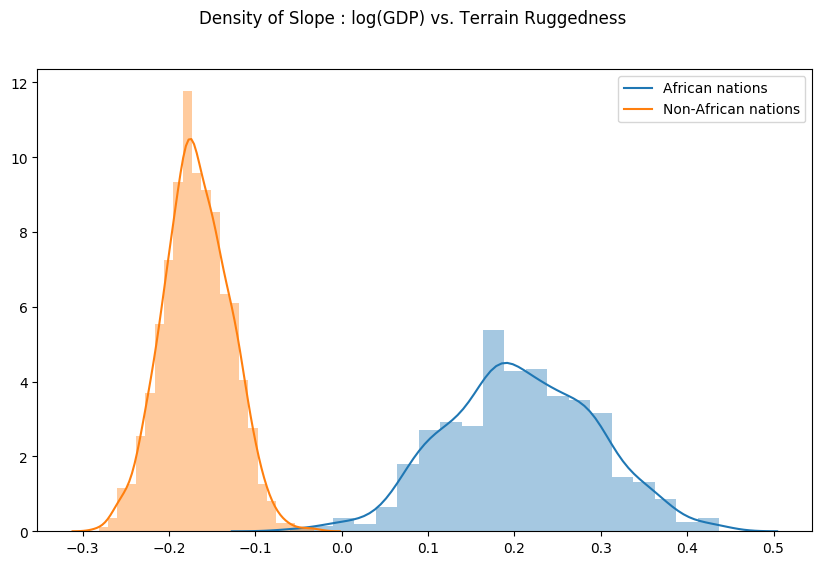
最后，让我们重新审视之前的问题，即地形崎岖度与 GDP 之间的关系对于模型参数估计的任何不确定性有多稳健。为此，我们绘制了考虑到非洲境内和境外国家地形崎岖程度的 GDP 对数斜率分布。如下所示，非洲国家的概率质量主要集中在正区域，其他国家反之亦然，这进一步证实了最初的假设。

[18]:

weight = samples["linear.weight"]
weight = weight.reshape(weight.shape[0], 3)
gamma_within_africa = weight[:, 1] + weight[:, 2]
gamma_outside_africa = weight[:, 1]
fig = plt.figure(figsize=(10, 6))
sns.distplot(gamma_within_africa, kde_kws={"label": "African nations"},)
sns.distplot(gamma_outside_africa, kde_kws={"label": "Non-African nations"})
fig.suptitle("Density of Slope : log(GDP) vs. Terrain Ruggedness");

_images/bayesian_regression_33_0.png

五、通过 TorchScript 进行模型服务

最后，请注意model、guide和Predictive实用程序类都是torch.nn.Module实例，并且可以序列化为TorchScript。

在这里，我们展示了如何将 Pyro 模型作为torch.jit.ModuleScript提供服务，它可以作为 C++ 程序单独运行，而无需 Python 运行时。

为此，我们将Predictive使用 Pyro 的效果处理库重写我们自己的简单版本的实用程序类。这使用：

poutinetrace用于捕获运行模型/指南代码的执行跟踪。
poutinereplay将模型中的位点调节为从引导轨迹中采样的值。

[19]:

from collections import defaultdict
from pyro import poutine
from pyro.poutine.util import prune_subsample_sites
import warnings


class Predict(torch.nn.Module):
    def __init__(self, model, guide):
        super().__init__()
        self.model = model
        self.guide = guide

    def forward(self, *args, **kwargs):
        samples = {}
        guide_trace = poutine.trace(self.guide).get_trace(*args, **kwargs)
        model_trace = poutine.trace(poutine.replay(self.model, guide_trace)).get_trace(*args, **kwargs)
        for site in prune_subsample_sites(model_trace).stochastic_nodes:
            samples[site] = model_trace.nodes[site]['value']
        return tuple(v for _, v in sorted(samples.items()))

predict_fn = Predict(model, guide)
predict_module = torch.jit.trace_module(predict_fn, {"forward": (x_data,)}, check_trace=False)

我们使用torch.jit.trace_module来跟踪该模块的方法，并使用torch.jit.saveforward保存它。可以使用 PyTorch 的 C++ API 加载此保存的模型，或者使用 Python API，如下所示。reg_predict.pttorch::jit::load(filename)

[20]:

torch.jit.save(predict_module, '/tmp/reg_predict.pt')
pred_loaded = torch.jit.load('/tmp/reg_predict.pt')
pred_loaded(x_data)

[20]:

(张量([9.2165]),
 张量([[-1.6612,-0.1498,0.4282]]),
 张量([ 7.5951, 8.2473, 9.3864, 9.2590, 9.0540, 9.3915, 8.6764, 9.3775,
          9.5473、9.6144、10.3521、8.5452、5.4008、8.4601、9.6219、9.7774、
          7.1958、7.2581、8.9159、9.0875、8.3730、8.7903、9.3167、8.8155、
          7.4433、9.9981、8.6909、9.2915、10.1376、7.7618、10.1916、7.4754、
          6.3473、7.7584、9.1307、6.0794、8.5641、7.8487、9.2828、9.0763、
          7.9250、10.9226、8.0005、10.1799、5.3611、8.1174、8.0585、8.5098、
          6.8656、8.6765、7.8925、9.5233、10.1269、10.2661、7.8883、8.9194、
         10.2866、7.0821、8.2370、8.3087、7.8408、8.4891、8.0107、7.6815、
          8.7497、9.3551、9.9687、10.4804、8.5176、7.1679、10.8805、7.4919、
          8.7088、9.2417、9.2360、9.7907、8.4934、7.8897、9.5338、9.6572、
          9.6604、9.9855、6.7415、8.1721、10.0646、10.0817、8.4503、9.2588、
          8.4489、7.7516、6.8496、9.2208、8.9852、10.6585、9.4218、9.1290、
          9.5631、9.7422、10.2814、7.2624、9.6727、8.9743、6.9666、9.5856、
          9.2518、8.4207、8.6988、9.1914、7.8161、9.8446、6.5528、8.5518、
          6.7168、7.0694、8.9211、8.5311、8.4545、10.8346、7.8768、9.2537、
          9.0776、9.4698、7.9611、9.2177、8.0880、8.5090、9.2262、8.9242、
          9.3966、7.5051、9.1014、8.9601、7.7225、8.7569、8.5847、8.8465、
          9.7494、8.8587、6.5624、6.9372、9.9806、10.1259、9.1864、7.5758、
          9.8258、8.6375、7.6954、8.9718、7.0985、8.6360、8.5951、8.9163、
          8.4661、8.4551、10.6844、7.5948、8.7568、9.5296、8.9530、7.1214、
          9.1401、8.4992、8.9115、10.9739、8.1593、10.1162、9.7072、7.8641、
          8.8606, 7.5935]),
 张量(0.9631))

让我们通过从加载的模块生成样本并重新生成之前的绘图来检查我们的Predict模块是否确实正确序列化。

[21]:

weight = []
for _ in range(800):
    # index = 1 corresponds to "linear.weight"
    weight.append(pred_loaded(x_data)[1])
weight = torch.stack(weight).detach()
weight = weight.reshape(weight.shape[0], 3)
gamma_within_africa = weight[:, 1] + weight[:, 2]
gamma_outside_africa = weight[:, 1]
fig = plt.figure(figsize=(10, 6))
sns.distplot(gamma_within_africa, kde_kws={"label": "African nations"},)
sns.distplot(gamma_outside_africa, kde_kws={"label": "Non-African nations"})
fig.suptitle("Loaded TorchScript Module : log(GDP) vs. Terrain Ruggedness");