笔记为自我总结整理的学习笔记,若有错误欢迎指出哟~
吴恩达课程笔记——深度学习概论、神经网络基础
- 一、概念区别
- 1.深度学习与机器学习
- 2.深度学习与神经网络
- 二、什么是神经网络
- 1.分类
- 2.特点
- 3.工作原理
- 4.神经网络示意图
- 5.神经网络进行监督学习
- 6.深度学习的发展
- 三、神经网络基础
- 1.二分分类(Binary Classification)
- 2.logistic回归
- 变量定义
- 损失函数(loss function)
- 成本函数(cost function)
- 3.梯度下降法(Gradient Decent)
- 4.计算图(Computation Graph)
- 5.单个样本的梯度下降法
- 6.m个样本的梯度下降法
- 7.logistic回归一次迭代的向量化形式
一、概念区别
1.深度学习与机器学习
深度学习 < 机器学习
机器学习:用数据或以往经验,优化计算机程序的性能标准
深度学习:学习样本数据的内在规律和表示层次,目标是让机器能够像人一样具有分析学习能力,能够识别文字、图像、声音等数据
2.深度学习与神经网络
神经网络和深度学习是机器学习常见算法中的两个,
“深度学习”训练神经网络
神经网络也改变了深度学习
神经网络:速度快
深度学习:思考能力强
二、什么是神经网络
人工神经网络(Artificial Neural Networks,简写为ANNs)也简称为神经网络(NNs)
1.分类
模型结构
前馈型网络(也称为多层感知机网络)、反馈型网络(也称为Hopfield网络)
学习方式
有监督学习、非监督、半监督学习
工作方式
确定性、随机性
时间特性
连续型、离散型
2.特点
大规模并行处理,分布式存储,弹性拓扑,高度冗余和非线性运算。因而具有很髙的运算速度,很强的联想能力,很强的适应性,很强的容错能力和自组织能力。
3.工作原理
- 必须先学习,再工作。
- 神经元间有连接权值,一开始是随机数,通过对训练结果正误的判断,改变随机数的大小。
- 有监督的学习:利用给定的样本标准进行分类或模仿
- 无监督的学习:只规定学习方式或某些规则,则具体的学习内容随系统所处环境 (即输入信号情况)而异,系统可以自动发现环境特征和规律性,具有更近似人脑的功能
4.神经网络示意图

每一个节点都可能与一个或多个神经元连接。用法是:输入x,得到y, 中间过程全由神经网络自身完成。
圆点叫做隐藏单元。
给神经网络足够的 (x,y) 样本,神经网络很善于计算从 x 到 y 的精确映射函数。
5.神经网络进行监督学习
分类与回归
分类的输出类型是离散数据,回归的输出类型是连续数据。
监督学习应用举例
实际估值、线上广告、图像判断、声音处理、机器翻译、自动驾驶
| 输入(x) | 输出(y) | 应用 |
|---|---|---|
| 房屋情况 | 价格 | 实际估值 |
| 广告,用户信息 | 是否点击(0/1) | 线上广告 |
| 图像 | 对象(1,…,1000) | 照片标记 |
| 音频 | 文字记录 | 语音识别 |
| 英语 | 中文 | 机器翻译 |
| 图像,雷达信息 | 其他车辆位置 | 自动驾驶 |
几种神经网络
卷积神经网络(Convolutional Neural Networks, CNN):图像处理
循环神经网络(Recurrent Neural Network, RNN):一维数据处理
混合神经网络(Hybrid Neural Network, HNN):汽车自动驾驶
6.深度学习的发展
驱动力:规模更大的模型、大量的标签数据
三个基本要素:数据量、计算速度、算法
三、神经网络基础
1.二分分类(Binary Classification)
-
输出结果只有两种:0/1
-
符号定义
- x(输入):图片的特征向量(列向量形式存储)
- y(输出):0/1


-
nx:特征向量x的维度
-
(x,y):一个单独的样本,x是nx维的特征向量,y是值1或0
-
mtrain:训练样本数
-
mtest:测试样本数
-
X:矩阵表示训练样本输入集,X.shape = (nx,m)
-
Y:矩阵表示训练样本输出集,Y.shape = (1,m)
-
目标:训练出一个分类器,以特征向量x为输入,预测输出结果y是1还是0
2.logistic回归
变量定义
当输出y为1或0时,用于监督学习的一种学习算法,目标是最小化模型预测与实验数据之间的误差。
logistic回归中使用的变量如下:
-
nx维输入特征向量:x
-
一维反馈结果:y(与x组对出现在输入训练集中)
-
nx维权重向量:w
-
阀值:b∈R
-
算法输出:y = σ(wTx + b)
-
sigmoid函数:
s = σ ( w T x + b ) = σ ( z ) = 1 1 + e − z s=σ(w^Tx+b)=σ(z)=\frac{1}{1+e^{-z}} s=σ(wTx+b)=σ(z)=1+e−z1

(wTx + b)是一个线性函数,但我们想要的是[0,1]的数。在神经网络算法中,我们常常使用sigmoid函数把一个函数映射到[0,1]区间上。
- 当z很大时,e-z→0,σ(z) = 1
- 当z很小时(z<0),e-z→∞,σ(z) = 0
- 当z = 0时,σ(z) = 0.5
损失函数(loss function)
回顾:
y
^
i
=
σ
(
w
T
x
i
+
b
i
)
=
σ
(
z
i
)
=
1
1
+
e
−
z
i
ŷ_i=σ(w^Tx_i+b_i)=σ(z_i)=\frac{1}{1+e^{-z_i}}
y^i=σ(wTxi+bi)=σ(zi)=1+e−zi1
G i v e n { ( x 1 , y 1 ) , ⋯ , ( x m , y m ) } , w e w a n t y ^ i ≈ y i Given\{(x_1,y_1),\cdots,(x_m,y_m)\},we\ want\ ŷ_i≈y_i Given{(x1,y1),⋯,(xm,ym)},we want y^i≈yi
损失函数计算每一个单独的训练样本的出错情况。预测输出 ŷi 与目标输出 yi 之间的差异
损失函数为:
L
(
y
^
i
,
y
i
)
=
−
[
y
i
l
o
g
y
^
i
+
(
1
−
y
i
)
l
o
g
(
1
−
y
^
i
)
]
L(ŷ_i,y_i)=-[y_ilogŷ_i+(1-y_i)log(1-ŷ_i)]
L(y^i,yi)=−[yilogy^i+(1−yi)log(1−y^i)]
分析该函数可得:
-
log1=0
-
如果 yi = 1,要使L→0,需要 ŷi →1
-
如果 yi = 0,要使L→0,需要 ŷi →0
成本函数(cost function)
为了训练参数w和b,需要定义成本函数。成本函数是整个训练集每个训练样本的损失函数的平均水平。
J
(
w
,
b
)
=
1
m
∑
i
=
1
m
L
(
y
^
i
,
y
i
)
=
−
1
m
∑
i
=
1
m
[
y
i
l
o
g
y
^
i
+
(
1
−
y
i
)
l
o
g
(
1
−
y
^
i
)
]
J(w,b)=\frac{1}{m}\sum_{i=1}^{m}{L(ŷ_i,y_i)}=-\frac{1}{m}\sum_{i=1}^{m}{[y_ilogŷ_i+(1-y_i)log(1-ŷ_i)]}
J(w,b)=m1i=1∑mL(y^i,yi)=−m1i=1∑m[yilogy^i+(1−yi)log(1−y^i)]
3.梯度下降法(Gradient Decent)
使用梯度下降法寻找 J 的最小值以及此时 w 和 b 的值。
对 w 和 b 进行如下迭代,直到 J 达到一个稳定的最小值,α为学习率
w
=
w
−
α
d
J
d
w
w=w-α\frac{dJ}{dw}
w=w−αdwdJ
b = b − α d J d b b=b-α\frac{dJ}{db} b=b−αdbdJ
4.计算图(Computation Graph)
从左向右:计算中间变量和成本函数 J 的值。

从右向左:计算 J 对各变量的导数。

d v = d J d v = 3 , d u = d J d v d v d u = 3 dv=\frac{dJ}{dv}=3,du=\frac{dJ}{dv}\frac{dv}{du}=3 dv=dvdJ=3,du=dvdJdudv=3
d a = d J d v d v d a = 3 × 1 = 3 da=\frac{dJ}{dv}\frac{dv}{da}=3\times1=3 da=dvdJdadv=3×1=3
d b = d J d v d v d u d u d b = 3 × 1 × 2 = 6 db=\frac{dJ}{dv}\frac{dv}{du}\frac{du}{db}=3\times1\times2=6 db=dvdJdudvdbdu=3×1×2=6
d c = d J d v d v d u d u d c = 3 × 1 × 3 = 9 dc=\frac{dJ}{dv}\frac{dv}{du}\frac{du}{dc}=3\times1\times3=9 dc=dvdJdudvdcdu=3×1×3=9
5.单个样本的梯度下降法
单个训练样本的损失函数和对应的参数w和b

d L d a = − y a + 1 − y 1 − a \frac{dL}{da}=-\frac{y}{a}+\frac{1-y}{1-a} dadL=−ay+1−a1−y
d a d z = a ( 1 − a ) \frac{da}{dz}=a(1-a) dzda=a(1−a)
d z = d L d z = d L d a d a d z = a − y dz=\frac{dL}{dz}=\frac{dL}{da}\frac{da}{dz}=a-y dz=dzdL=dadLdzda=a−y
d L d w 1 = d L d z d z d w 1 = x 1 d z , d L d w i = x i d z \frac{dL}{dw_1}=\frac{dL}{dz}\frac{dz}{dw_1}=x_1dz,\frac{dL}{dw_{i}}=x_{i}dz dw1dL=dzdLdw1dz=x1dz,dwidL=xidz
d b = d z db=dz db=dz
w i = w i − α d L d w i w_i=w_i-α\frac{dL}{dw_i} wi=wi−αdwidL
b = b − α d L d b b=b-α\frac{dL}{db} b=b−αdbdL
6.m个样本的梯度下降法
randomly initialize w and b
repeat these until J is small enough:
J=0
dw=0
db=0
#计算m个样本在目前w和b情况下的成本函数
for i=1 to m: #m个样本
z[i]=w*x[i]+b
a[i]=σ(z[i])
J+=L(a,y[i])
dz=a[i]-y[i]
for j=1 to n_x: #样本x的维度n_x
dw[j]+=x[i][j]*dz
db += dz
#得到当前成本函数值(和这一轮用来迭代的dw、db)
J /= m
for j=1 to n_x:
dw[j] /= m
db /= m
#对w和b进行迭代
for i=1 to m:
w[i] = w[i] - α * dw
b = b - α * db
这里显式地使用了许多for循环,对运行效率有很大负面影响。接下来会介绍如何使用向量化技术来为训练提速。
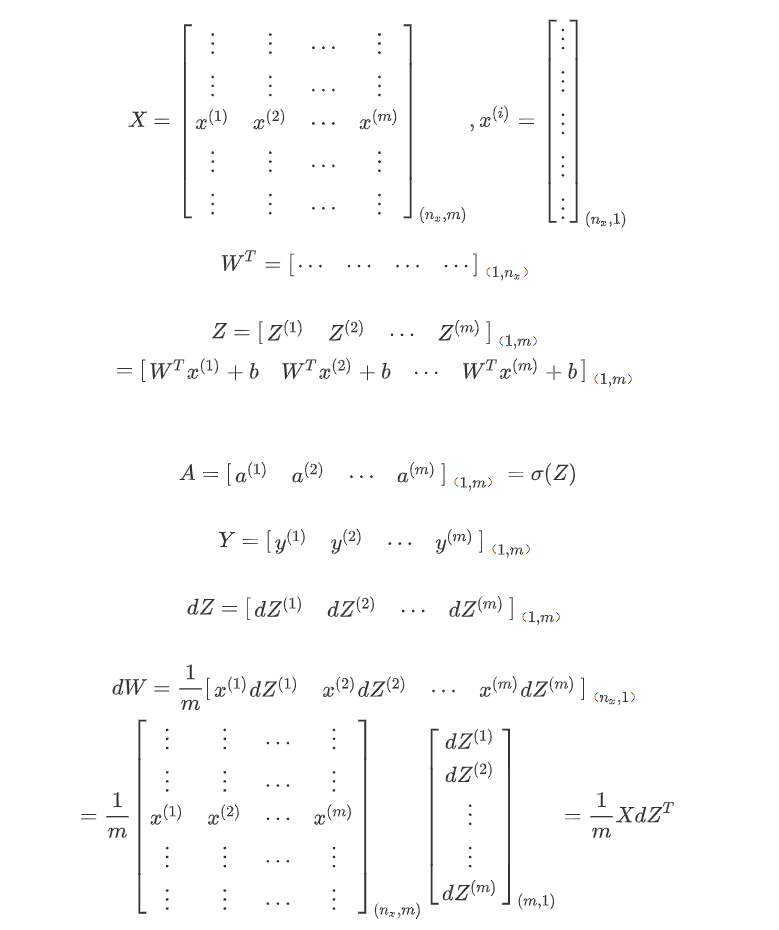
7.logistic回归一次迭代的向量化形式
Z = w^T * X + b
= np.dot(w.T, X) + b
A = σ(Z)
dZ = A - Y
dw = 1/m * X * dZ^T
db = 1/m * np.sum(dZ)
w = w - αdw
b = b - αdw
推导过程如下: