笔记为自我总结整理的学习笔记，若有错误欢迎指出哟~

笔记链接

【深度学习】吴恩达课程笔记(一)——深度学习概论、神经网络基础
【深度学习】吴恩达课程笔记(二)——浅层神经网络、深层神经网络

六、参数VS超参数

1.参数和超参数的区别

参数（Parameters）是指模型内部需要学习的权重值。在训练过程中，模型通过反向传播算法来更新这些权重值以最小化损失函数。例如，在线性回归模型中，参数就是回归系数（即斜率和截距），在神经网络模型中，参数就是每个神经元之间的权重值。

超参数（Hyperparameters）是指模型训练过程中需要设置的一些参数，这些参数不能通过反向传播算法来更新，而是需要手动调整。超参数的选择可以影响模型的性能和训练效果。例如，在神经网络模型中，超参数包括学习率、批量大小、隐藏层大小等。

参数和超参数的区别在于，参数是模型内部需要学习的权重值，而超参数是模型训练过程中需要手动设置的一些参数。参数的值是通过训练数据自动学习得到的，而超参数的值需要手动调整，通常需要多次尝试和实验才能找到最佳的超参数组合。

2.什么是超参数？

超参数（Hyperparameters）是机器学习算法中的一种参数，它们用于控制模型训练过程的行为，而不是直接由数据决定。与模型的权重（即学习参数）不同，超参数通常在训练之前设定，并且需要手动调整。

超参数的选择对模型的性能和训练效果有很大影响。不同的超参数组合可能导致不同的模型表现，因此选择合适的超参数非常重要。

常见的超参数包括：

1. 学习率（Learning Rate）：控制模型在每次迭代中更新权重的步长大小。
2. 正则化参数（Regularization Parameter）：用于控制模型的复杂度，防止过拟合。
3. 批量大小（Batch Size）：指定每次迭代中用于更新权重的样本数量。
4. 迭代次数（Number of Iterations）：定义模型在训练集上迭代的次数。
5. 隐藏层大小（Size of Hidden Layers）：适用于神经网络模型，用于设置隐藏层的节点数量。
6. 决策树的深度（Depth of Decision Trees）：适用于决策树模型，用于控制树的最大深度。
7. 核函数选择（Choice of Kernel Function）：适用于支持向量机模型，用于定义数据之间的相似度。
8. 聚类算法中的簇数量（Number of Clusters）：适用于聚类算法，用于指定期望的簇数量。

选择合适的超参数通常需要通过试验和交叉验证来确定最佳组合。通常，可以使用网格搜索、随机搜索或贝叶斯优化等技术来自动化超参数调整的过程，以找到最佳的超参数组合。

3.如何寻找超参数的最优值？

寻找超参数的最优值是一个重要且挑战性的任务。以下是一些常用的方法和技巧：

1. 网格搜索（Grid Search）：网格搜索是一种简单直观的方法，它通过指定超参数的候选值组成的网格来遍历所有可能的组合。对于每个组合，使用交叉验证来评估模型性能，并选择具有最佳性能的超参数组合。
2. 随机搜索（Random Search）：与网格搜索相比，随机搜索不是遍历所有可能的组合，而是在给定的超参数空间中随机选择一组超参数进行评估。通过随机选择，可以更高效地探索超参数空间，并找到良好的超参数组合。
3. 贝叶斯优化（Bayesian Optimization）：贝叶斯优化是一种基于贝叶斯推断的序列模型优化方法。它通过建立一个代理模型来估计目标函数（例如模型的性能），并使用贝叶斯推断来指导下一次选择哪个超参数组合进行评估。贝叶斯优化可以有效地在较少的迭代次数内找到最优的超参数组合。
4. 交叉验证（Cross-Validation）：交叉验证是一种评估模型性能的技术，也可以用于超参数调整。通过将训练数据分成多个子集，然后在每个子集上轮流进行模型训练和验证，可以获得更稳健的性能评估结果。在超参数调整过程中，使用交叉验证来评估每个超参数组合的性能，并选择具有最佳性能的组合。
5. 学习曲线（Learning Curve）：学习曲线是一种可视化工具，用于分析模型在不同超参数设置下的性能变化。通过绘制训练集大小和模型性能之间的关系，可以帮助判断模型是否过拟合或欠拟合，并指导超参数的选择。
6. 自动化调参工具：还有一些自动化调参工具可用于帮助寻找最优的超参数组合，例如Hyperopt、Optuna和scikit-optimize等。这些工具结合了上述方法，并提供了更高级的优化算法和搜索策略，以加速超参数调整的过程。

需要注意的是，超参数的最优值是相对的，它取决于数据集、模型类型和具体任务等因素。因此，超参数调整通常需要反复尝试和实验，以找到最适合特定情况的超参数组合。

七、深度学习的实践层面

1.训练 / 验证 / 测试集(Train / Dev / Test)

训练集：训练模型

验证集：验证算法正确性

测试集：测试算法效率

2.偏差 / 方差 (Bias / Variance)

• 偏差大：训练集上的结果较差
• 方差大：验证集上的结果比训练集上的差的较多

Train set error	Dew set error	偏差 / 方差
1%	11%	高方差
15%	16%	高偏差
15%	30%	高方差、高偏差
0.5%	1%	低方差、低偏差

具体例子

偏差 / 方差	图像
高偏差（欠拟合）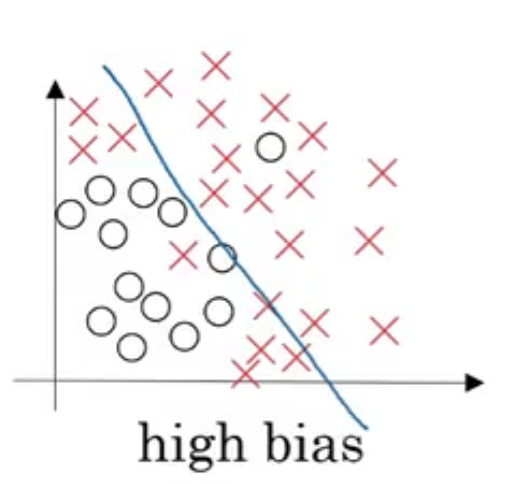
适度拟合
高方差（过拟合）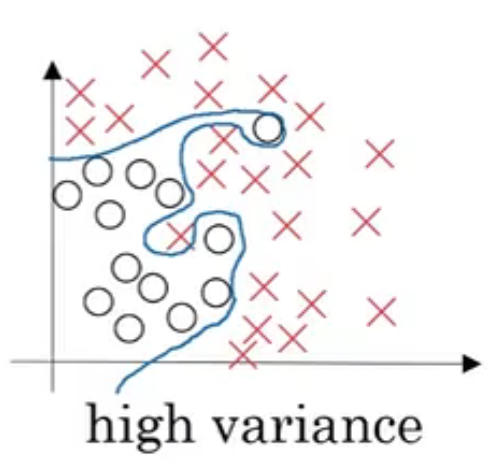
高偏差 & 高方差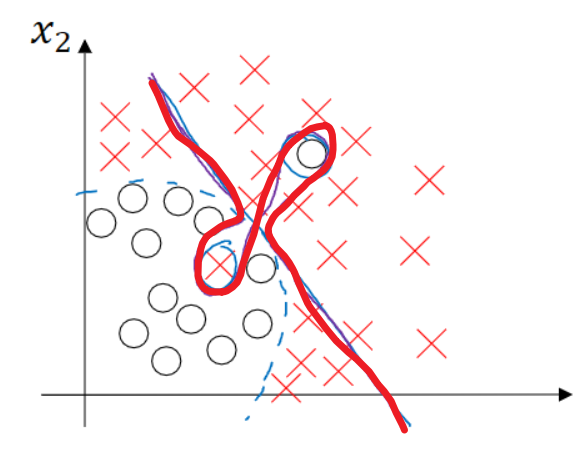

3.机器学习基础

遇到的问题	可尝试的解决办法
高偏差（欠拟合）	1.更大的神经网络 2.更多的神经网络层数
高方差（过拟合）	1.更多训练数据 2.正则化

4.L2正则化

范数的概念

在数学中，范数（Norm）是一种将向量映射到非负实数的函数。在机器学习和优化问题中，范数常用于衡量向量的大小或长度。

Lp 范数：

L1 范数：也称为曼哈顿范数（Manhattan Norm）。L1 范数在一些特定场景下具有稀疏性，能够产生稀疏解。

L2 范数：也称为欧几里得范数（Euclidean Norm）。L2 范数在许多优化问题中都有很好的性质，例如它可以用于正则化、最小二乘问题等。

L∞ 范数：也称为切比雪夫范数（Chebyshev Norm），定义为向量中各个元素绝对值的最大值。L∞ 范数可以用于约束向量各个元素的最大值。

在机器学习中，范数常用于正则化、特征选择、最小二乘问题等。例如，在线性回归模型中，可以使用 L1 或 L2 范数对模型参数进行正则化，以避免过拟合。在特征选择中，可以使用 L1 范数来选择具有重要影响的特征，从而减少特征数量，提高模型的泛化能力。

正则化的定义

在机器学习中，正则化（Regularization）是一种常用的技术，旨在减少模型的复杂度，避免过拟合，提高模型的泛化能力。正则化通过在损失函数中加入一个惩罚项来实现。

通常，机器学习模型的目标是最小化训练误差（即损失函数），但是如果模型过于复杂，则可能会在训练数据上表现良好，但在新数据上表现不佳，这种现象称为过拟合（高方差）。为了避免过拟合，可以使用正则化技术来限制模型的复杂度。

常见的正则化方法包括：

1. L1 正则化：也称为 Lasso 正则化，通过在损失函数中添加 L1 范数惩罚项，使得模型参数中的一些权重变成 0，从而实现特征选择和稀疏性。
2. L2 正则化：也称为 Ridge 正则化，通过在损失函数中添加 L2 范数惩罚项，使得模型参数的值变得更小，从而避免过拟合。
3. 弹性网络正则化：结合了 L1 和 L2 正则化，可以同时实现特征选择和过拟合控制。

L2正则化

$$\begin{gathered} ||•|{|}_F^2:矩阵的弗罗贝尼乌斯范数（Frobenius） \\ ||W^{[L]}|{|}_F^2=\sum _{i=1}^{n^{[l-1]}}\sum _{j=1}^{n^{[l]}}(W_{ij}^{[l]}{)}^2 \\ W:(n^{[l-1]},n^{[l]}) \end{gathered}$$

重定义损失函数为
$$\begin{gathered} \lambda :regularizationparameter \\ J(w,b)=\frac{1}{m}\sum _{i=1}^{m}L({\hat{y}}_i,y_i)+\frac{\lambda }{2m}\sum _l||W^{[l]}|{|}_F^2 \\ d{W}^{[l]}=(frompropagation)+\frac{\lambda }{m}{W}^{[l]} \\ {W}^{[l]}=W^{[l]}-\alpha d{W}^{[l]} \\ =W^{[l]}-\alpha [(frompropagation)+\frac{\lambda }{m}{W}^{[l]}] \\ =W^{[l]}-\frac{\alpha \lambda }{m}{W}^{[l]}-\alpha (frompropagation) \\ =(1-\frac{\alpha \lambda }{m})W^{[l]}-\alpha (frompropagation) \end{gathered}$$
L2正则化对dW进行了增大处理，使得W的值受到惩罚而变小。L2正则对特征系数做了比例的缩放，这会让系数趋向变小但不会变为0，因此L2正则会让模型变得更简单，防止过拟合，而不会起到特征选择的作用。

正则化为什么可以预防过拟合

若激活函数选择𝑡𝑎𝑛ℎ(𝑧)。如果正则化参数变得很大，参数𝑊很小，𝑧也会相对变小，𝑡𝑎𝑛ℎ会相对呈线性，整个神经网络会计算离线性函数近的值，不是一个极复杂的高度非线性函数，不会发生过拟合。
$$Z^{[l]}=W^{[1]}{A}^{[l-1]}+b^{[l]}$$

5.dropout（随机失活）

基本步骤

他的基本步骤是在每一次的迭代中，随机删除一部分节点，只训练剩下的节点。每次迭代都会随机删除，每次迭代删除的节点也都不一样，相当于每次迭代训练的都是不一样的网络，通过这样的方式降低节点之间的关联性以及模型的复杂度，从而达到正则化的效果。

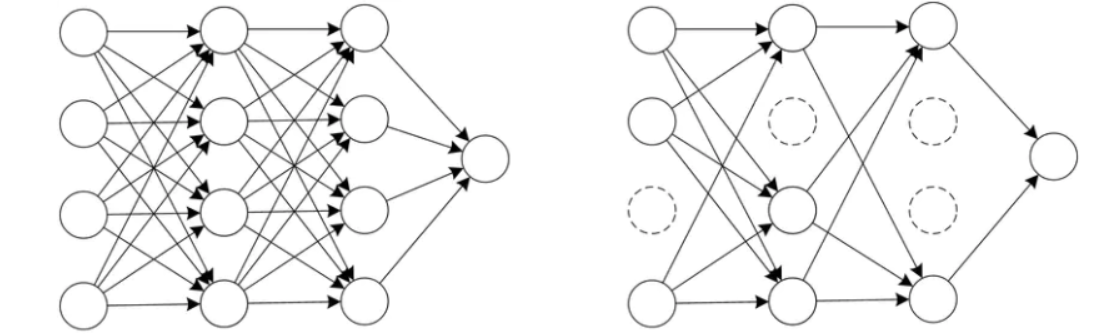
• 设置一个超参数 keep_prob：每层节点随机保留的比例

• 将 keep_prob 设置为 0.7，那么就会随机30%的节点消失

• 将这一层的参数矩阵与根据 keep_prob 生成的 {0, 1} 矩阵逐点乘积

• 前向传播与反向传播都需要做以上的操作

Dropout的缺点

1. 网络训练时间增加：在使用 Dropout 时，由于每次训练迭代都需要随机屏蔽一部分神经元，因此会导致网络的训练时间增加。这是因为在每个迭代中，都需要更新被屏蔽神经元的权重，从而导致计算量的增加。
2. 需要适当调整学习率：由于 Dropout 可能导致部分神经元的输出值变为 0，因此在使用 Dropout 时，需要适当调整学习率。如果学习率过高，可能会导致网络无法收敛；如果学习率过低，可能会导致网络收敛速度过慢。
3. 内存消耗增加：在使用 Dropout 时，为了保存被屏蔽的神经元的状态，需要占用额外的内存空间。对于大型的神经网络，这可能会导致内存消耗的增加，限制了模型的规模和训练效率。
4. 不适用于所有类型的层：Dropout 技术通常适用于全连接层和卷积层，但对于循环神经网络（RNN）等具有时间依赖性的层，Dropout 的应用可能会更加复杂。在 RNN 中，由于时间步之间的依赖关系，随机屏蔽神经元可能会导致信息丢失和模型性能下降。

如何实施 dropout

inverted dropout（反向随机失活）

一个三层（𝑙 = 3）网络来举例说明

• 定义向量𝑑，𝑑 ^[3]表示一个三层的 dropout 向量

  d3 = np.random.rand(a3.shape[0],a3.shape[1]) < keep-prob
  

• 从第三层中获取激活函数它𝑎 ^[3]，让𝑑 ^[3]中 0 元素与𝑎 ^[3]中相对元素归零。

  a3 =np.multiply(a3,d3)
  

• 向外扩展𝑎 ^[3]，用它除以 keep-prob 参数。

  • 原因：𝑧 ^[4] = 𝑤 ^[4]𝑎 ^[3] + 𝑏 ^[4]，为了不影响𝑧^[4]的期望值，我们需要用𝑤^[4]𝑎 ^[3] /keep-prob，𝑎 ^[3] 的期望值不会变

  a3/= keep-prob
  

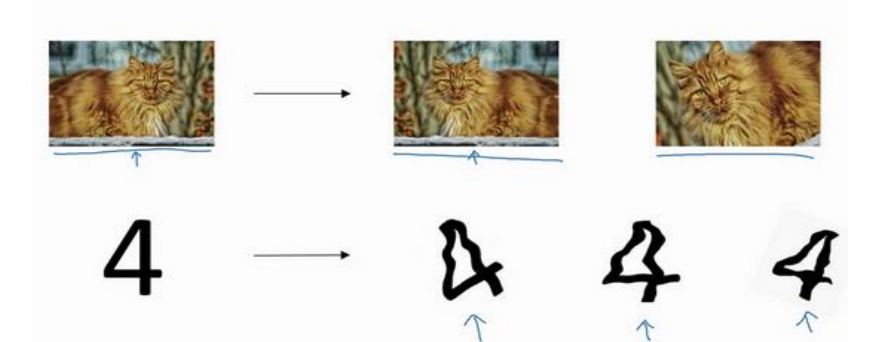
6.其他正则化方法

数据扩增

early stopping

提前终止可能是最简单的正则化方式，他适用于模型的表达能力很强的时候。这种情况下，一般训练误差会随着训练次数的增多逐渐下降，而测试误差则会先下降而后再次上升。我们需要做的就是在测试误差最低的点停止训练即可。

7.归一化输入

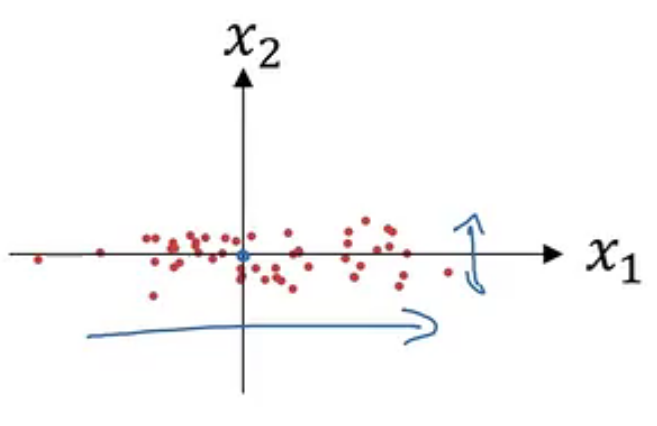
假设我们在处理深度学习相关问题时的输入有两个属性，分别为x1与x2。具体形式如下图所示。

零均值化	归一化方差

步骤

1. 零均值化：使样本数据均匀分布到x轴上下
   $$\begin{gathered} x^{(i)}为输入向量 \\ \mu =\frac{1}{m}\sum _{i-1}^m{x}^{(i)} \\ x=x-\mu \end{gathered}$$

2. 归一化方差：使样本数据均匀分布到-1到1之间
   $$\begin{gathered} {\sigma }^2=\frac{1}{m}\sum _{i-1}^m{x}^{(i)2} \\ x/={\sigma }^2 \end{gathered}$$

目的

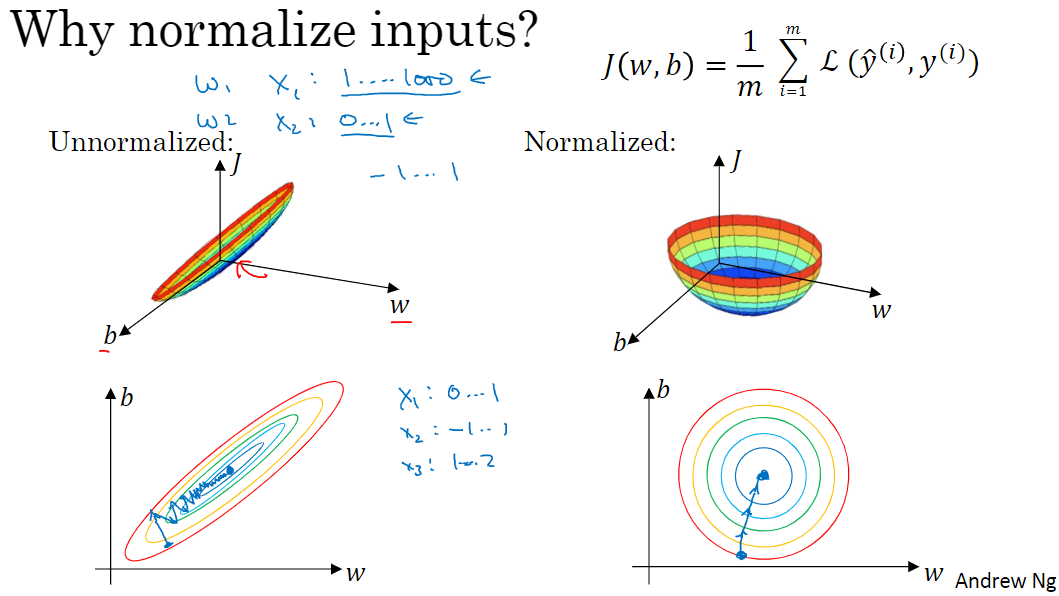
如果在图片左侧的情况下使用优化算法减少梯度，就必须使用一个非常小的学习率，那将会增加许多迭代次数。

使用归一化处理后损失函数的梯度可能会变得比较均匀，就像图片右侧所示。一个圆的球形轮廓，那么不论从哪个位置开始，优化算法往往都能更快的找到最优值。

综上来说，在一些特殊数据中，例取值范围差异较大等，需要进行正则化处理，以此加快梯度下降的速度。

注意：用归一化方式去处理了训练集，那么一定要用相同的方式去处理测试集。

8.梯度消失/梯度爆炸（Vanishing / Exploding gradients）

定义

$$\hat{y}=W^{[l]}{W}^{[L-1]}{W}^{[L-2]}\dots W^{[3]}{W}^{[2]}{W}^{[1]}x$$

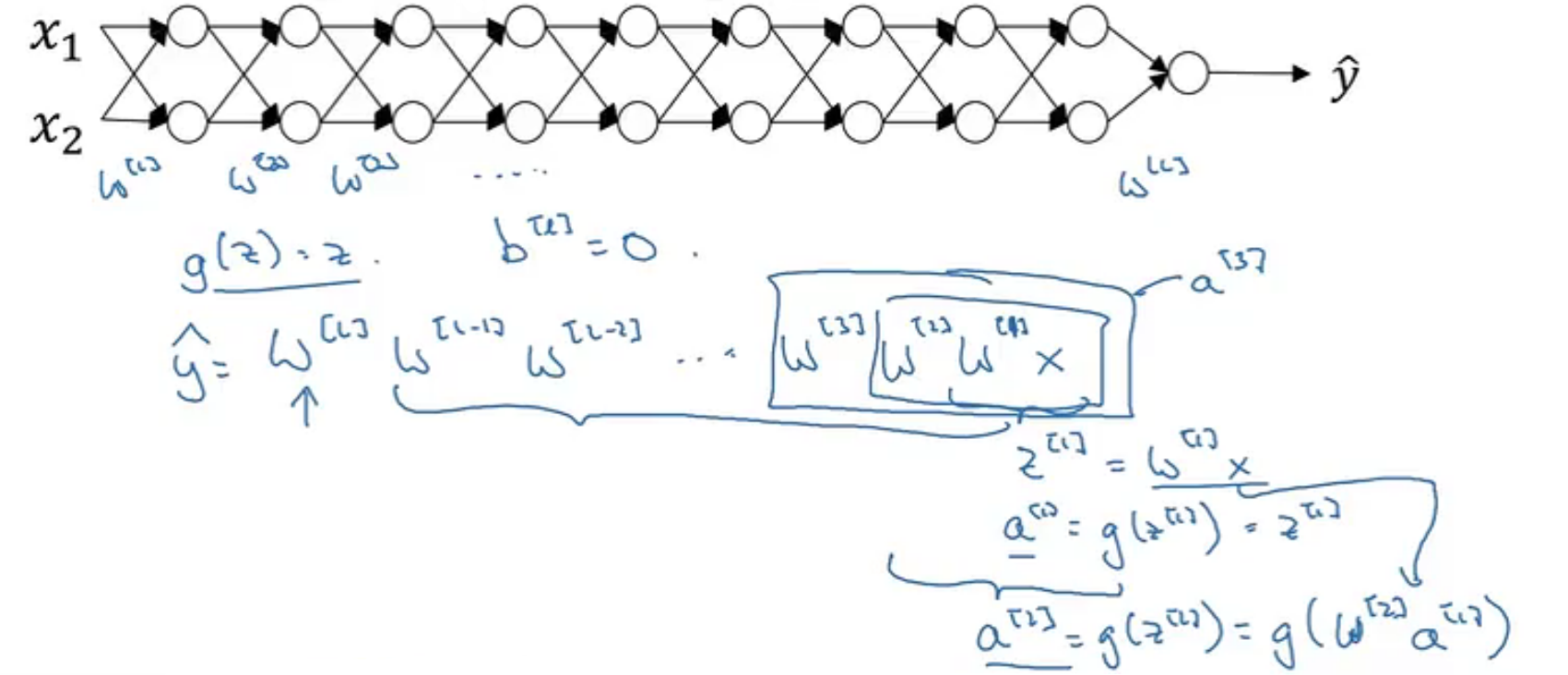
若W是大于1的单位矩阵：

前向传播中，激活函数的值会以指数形式增长，即爆炸

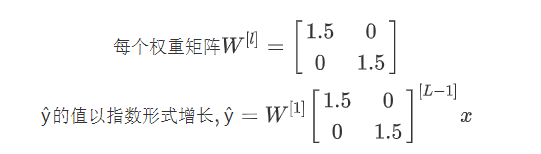
若W是小于1的单位矩阵：

前向传播中，激活函数的值会以指数形式减小，即消失

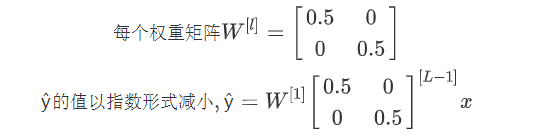
解决方法：权重初始化（Weight Initialization）

对第 l 层的W变量的初始化

若第 l 层使用relu激活函数，建议使用：
$$W^{[l]}=np.random.randn(shape)\ast np.sqrt(\frac{2}{n^{[l-1]}})$$
若第 l 层使用tanh激活函数，建议使用：
$$W^{[l]}=np.random.randn(shape)\ast np.sqrt(\frac{1}{n^{[l-1]}})$$

理由

这种计算使得W中的值被初始化为接近1的数，使得它不容易出现梯度爆炸或消失的情况。

初始化Tips

• 随机初始化可以破坏对称性，保证不同隐藏单元能学到不同的东西
• 不要用过大的值初始化
• He初始化对使用ReLU激活函数的网络非常有效

9.梯度校验

梯度的数值逼近（Numerical approximation of gradients）

假设𝜃 = 1，𝜀的值为 0.01。

不增大 𝜃 的值，而是在 𝜃 右侧，设置一个 𝜃 + 𝜀，在 𝜃 左侧，设置 𝜃 − 𝜀

得到的不是一个单边公差而是一个双边公差

$$\begin{gathered} f(\theta )={\theta }^3 \\ 当\theta =1时，g(\theta )=3{\theta }^2=3 \end{gathered}$$

$$g(\theta )=f^{\prime }(\theta )=\frac{f(\theta +ϵ)-f(\theta -ϵ)}{2ϵ}=\frac{f(1.01{)}^3-f(0.99{)}^3}{2\times 0.01}=3.0001$$

结论

• 双边公差，𝑔(𝜃)的值为3.0001，逼近误差是0.0001
• 单边公差，即从𝜃到𝜃 + 𝜀之间的误差，𝑔(𝜃)的值为3.0301，逼近误差是 0.03，不是 0.0001
• 使用双边误差的方法更逼近导数

梯度检验（Gradient checking）

• 𝑊^[1]，𝑏 ^[1]……𝑊^[𝑙]，𝑏 ^[𝑙]，把所有参数转换成一个巨型向量𝜃。得到了一个𝜃的代价函数𝐽（即𝐽(𝜃)）
• d𝑊^[1]，d𝑏 ^[1]……d𝑊^[𝑙]，d𝑏 ^[𝑙]，把所有参数转换成一个巨型向量d𝜃。
• d𝜃 与 𝜃 维度相同

𝑑𝜃和代价函数𝐽的梯度或坡度有什么关系？
$$J(\theta 1,\theta 2,\theta 3,\dots \dots )$$

$$\begin{gathered} foreachi: \\ d{\theta }_{appox}[i]=\frac{J({\theta }_1,{\theta }_2,\cdots ,{\theta }_i+ϵ,\cdots )-J({\theta }_1,{\theta }_2,\cdots ,{\theta }_i-ϵ,\cdots )}{2ϵ} \end{gathered}$$

将其与dθ进行比较，判断该数是否足够小。
$$\frac{||d{\theta }_{appox}-d\theta |{|}_2}{||d{\theta }_{appox}|{|}_2+||d\theta |{|}_2}$$
分子使用了欧几里的距离，分母存在的意义是使得整体数字变成一个比率，而不至于过大。

梯度检验应用的注意事项

• 不要在训练中使用梯度检验，它只用于调试。

  • 因为梯度检测使用大量for loop，非常耗费时间

• 如果算法的梯度检验失败，要检查所有项，检查每一项，并试着找出 bug

  • 找到使得矩阵dθ_appox与矩阵dθ相差过大的那列向量，顺藤摸瓜找出导致梯度检测失败的错误方程

• 如果使用正则化，记得在cost function中添加正则项

• 梯度检验不能和dropout一起用

  • 因为dropout会隐藏隐层单元的部分子集，而J被定义为计算所有隐层的损失程度。dropout会使每一轮的J值变化不那么稳定，可能会导致梯度检验晕头转向
  • 解决方法：把dropout中的keepprob设成1，然后进行梯度检验、检验函数的正确性。然后寄希望于dropout会对调好的模型有好的影响，再把dropout加回去。

• 有时候W、b在比较小的时候运行正常，当训练一段时间后，W、b变大了之后运行不正常了。

  • 可以在运行随机初始化参数的时候进行梯度检验，在训练一段时间后再进行梯度检验。