Part.I Introduction

首先要了解一下下面的知识：

• 1 位有两种状态：0 或 1
• 1 字节（byte） = 8 位（bit）
• $2^7=128$；$2^8=512$；$2^{16}=65536$；$2^{32}=4.3\times 10^9$；$2^{63}=9\times 10^{18}$；$2^{64}=1.8\times 10^{19}$；
• float 在计算机中一般用 4 个字节存储，其表示范围为 [-3.4028235E38, 3.4028235E38]，精确范围是[-340282346638528859811704183484516925440, 340282346638528859811704183484516925440]
• int 在计算机中也是用 4 个字节存储的，它还不能表示小数，它的存储范围为 [-2147483648‬, 2147483647]，一共是 $2^{32}=4294967296$ 种可能，为什么 float 既能表示小数，并且其表示范围还那么大呢？因为间隔！int 的间隔固定为1，float 的间隔是不是等间距的，它在 0 的附近间距小，在远离 0 的位置间距大（实际上，因为某些原因，float 能精确表示的数还不足 $2^{32}=4294967296$ 种¹）。
• 上面提到，float 的间隔不是等间距的，在表示数据很大的时候，这个间隔有可能达到几百几千甚至更大，那么间隔中间的数怎么表示呢？就近原则，即在 float 『能表示的数』中寻找最接近『要表示的数』的数，那么就用这个数来表示『要表示的数』。比如，4294967244.001 和 4294967295.009 均用 4294967296.000000 表示！
• float 的精度为7，这句话的含义是 float 至少保证 7 位有效数字是准确的！

---

Part.II 原理

float 在计算机中一般是用 4 个字节进行存储的，也就是 32 位，其中第 1 位为符号位，第 2-9 位（共 8 位）用来表示指数，第 10-32（共 23 位）用来表示尾数。下图形象地表示了 float 各个位发挥的作用：

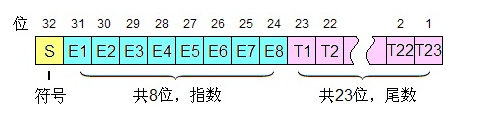
符号位很好理解，就是用 0 表示正数，用 1 表示负数；那么指数和尾数怎么理解呢？

首先我们知道常用的十进制科学计数法是将所有的数字转换成 $(\pm )a.b\times 10^c$ 的形式，其中 a 的范围是 1-9 共 9 个整数，b 是小数点后的所有数字，c 是 10 的指数。而计算机中存储的都是二进制数据，所以 float 存储的数字都要先转化成 $(\pm )a.b\times 2^c$，由于二进制中最大的数字就是1，所以表示法可以写成 $(\pm )1.b\times 2^c$ 的形式，float 要想存储小数就只需要存储 (±)，b 和 c 就可以了。

所以上面将 32 位划分成了三块，第一块存储符号，第二块存储指数 c，第三块存储指数 b！

---

举个例子，我们来表示8.25

• 整数部分为 8，二进制表示为1000；
• 小数部分为 0.25，小数部分的二进制表示计算方法和整数部分的计算方法恰恰相反，整数部分转换二进制的时候是不断除以 2 得到的，这里就是不断乘以2：0.25*2 = 0.5，整数部分为0，记下：0；0.5*2 = 1.0，整数部分为1，记下：1，所以 0.25 的二进制表示即为 0.01（1*2^{-2}）
• 于是8.25的(伪)二进制表示为1000.01
• 根据十进制的科学计数法，二进制的科学计数法可以进行如下类比：1000.01=1.00001*2^3
• 基于上述，我们便可以直接写出8.25的二进制表示了。因为8.25是正数，所以符号位为0；指数为3(3+127=130)，所以1000 0010（130的二进制表示）；小数位为 00001，因为要用 23 位来表示它，所以需后补 0，所以0000 1000 0000 0000 0000 000
• 所以8.25的二进制表示为0 1000 0010 0000 1000 0000 0000 0000 000

Part.III 代码验证

下面是一个大佬用 C 语言写的一个验证代码²：

#include <stdio.h>
int main()
{
    float a = 1;
    unsigned int s, e, i;
    char b[33], c, d;
    while (a)
    {
        printf("输入一个浮点数(0退出):");
        scanf("%f", &a);
        s = e = *((int *)&a);           // 强制类型转换到无符号整数
        b[32] = 0;
        for (i = 32; i; i--, s /= 2)
            b[i - 1] = s % 2 + '0';     // 十进制二进制转换
        printf("内存:%f=%s\n", a, b);
        printf("符号:%c\n", b[0]);
        c = b[9];
        b[9] = 0;
        d = ((e & 0x7f800000) >> 23) - 127;
        printf("指数:%s   (浮点移动位数%d,>0右移,<0左移)\n", b + 1, d);
        b[9] = c;
        printf("尾数:%s   (不含最前面隐含1)\n小数:", b + 9);
        d++;
        b[8] = '1';
        for (i = 31; i > 9 && b[i] == '0'; i--)
            ;
        b[i + 1] = 0; // 消尾0
        if (b[0] == '1')
            printf("-"); // 负数
        if (d > 0) // 小数点浮动
        { // 小数点右移
            for (i = 0; i < d; i++)
                printf("%c", b[i + 8]);
            printf(".%s （手工转换为十进制方法是：小数点前乘2，小数点后除以2）\n\n", b + i + 8);
        }
        else
        { // 小数点左移
            printf("0.");
            for (; d; d++)
                printf("0");
            printf("%s （手工转换为十进制方法是：小数点前乘2，小数点后除以2）\n\n", b + 8);
        }
    }
}

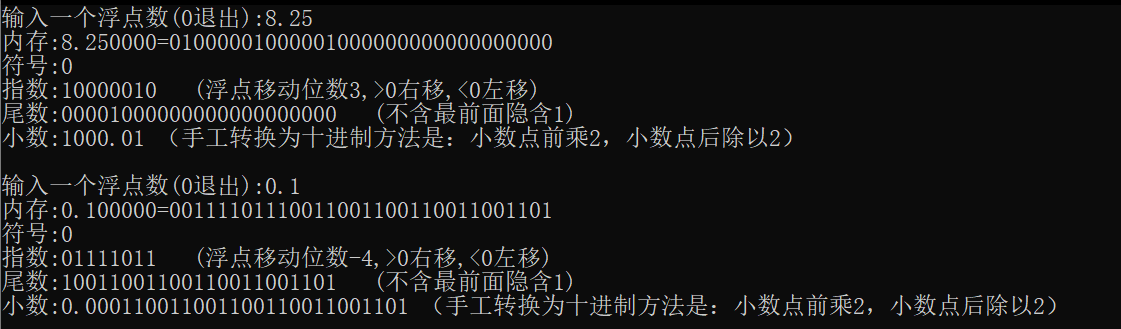
下面是验证结果：

Reference

---

1. float的精度和取值范围 ↩︎

2. 如何利用c语言验证一个数的浮点表示？ - lowxiong@知乎 ↩︎