文心一言 VS 讯飞星火 VS chatgpt （122）-- 算法导论10.4 3题

news2024/9/23 3:17:05

三、用go语言，给定一个n结点的二叉树，写出一个 O(n)时间的非递归过程，将该树每个结点的关键字输出。可以使用一个栈作为辅助数据结构。

文心一言：

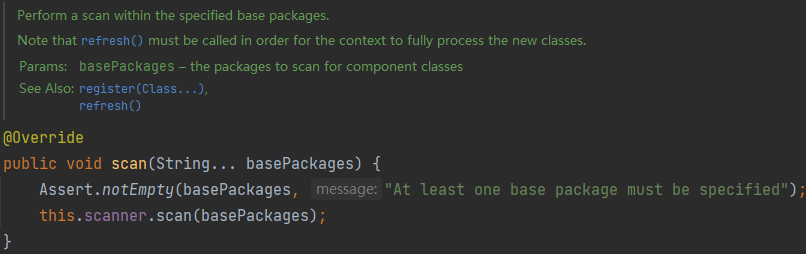
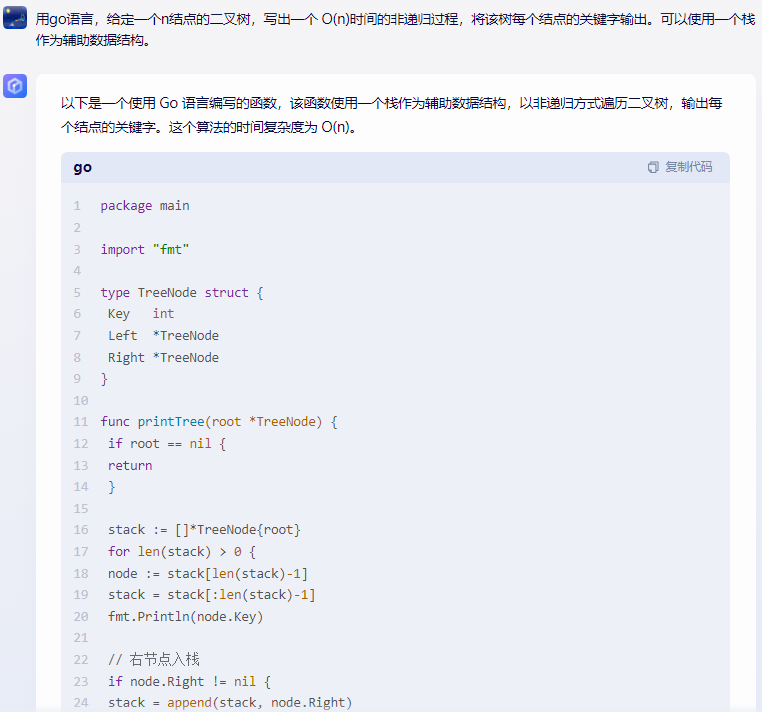
以下是一个使用 Go 语言编写的函数，该函数使用一个栈作为辅助数据结构，以非递归方式遍历二叉树，输出每个结点的关键字。这个算法的时间复杂度为 O(n)。

package main  
  
import "fmt"  
  
type TreeNode struct {  
 Key   int  
 Left  *TreeNode  
 Right *TreeNode  
}  
  
func printTree(root *TreeNode) {  
 if root == nil {  
 return  
 }  
  
 stack := []*TreeNode{root}  
 for len(stack) > 0 {  
 node := stack[len(stack)-1]  
 stack = stack[:len(stack)-1]  
 fmt.Println(node.Key)  
  
 // 右节点入栈  
 if node.Right != nil {  
 stack = append(stack, node.Right)  
 }  
 // 左节点入栈  
 if node.Left != nil {  
 stack = append(stack, node.Left)  
 }  
 }  
}

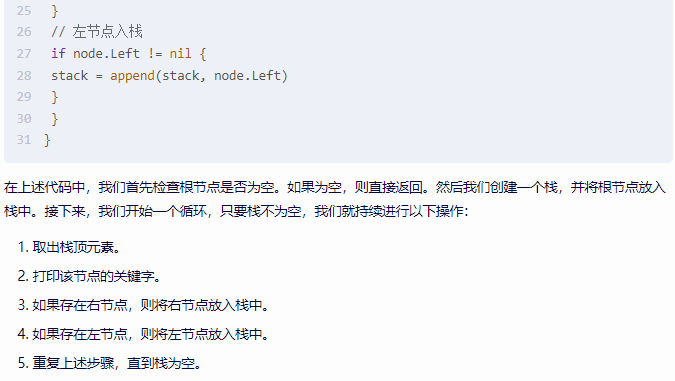
在上述代码中，我们首先检查根节点是否为空。如果为空，则直接返回。然后我们创建一个栈，并将根节点放入栈中。接下来，我们开始一个循环，只要栈不为空，我们就持续进行以下操作：

1.取出栈顶元素。

2.打印该节点的关键字。

3.如果存在右节点，则将右节点放入栈中。

4.如果存在左节点，则将左节点放入栈中。

5.重复上述步骤，直到栈为空。

在这里插入图片描述

在这里插入图片描述

讯飞星火：

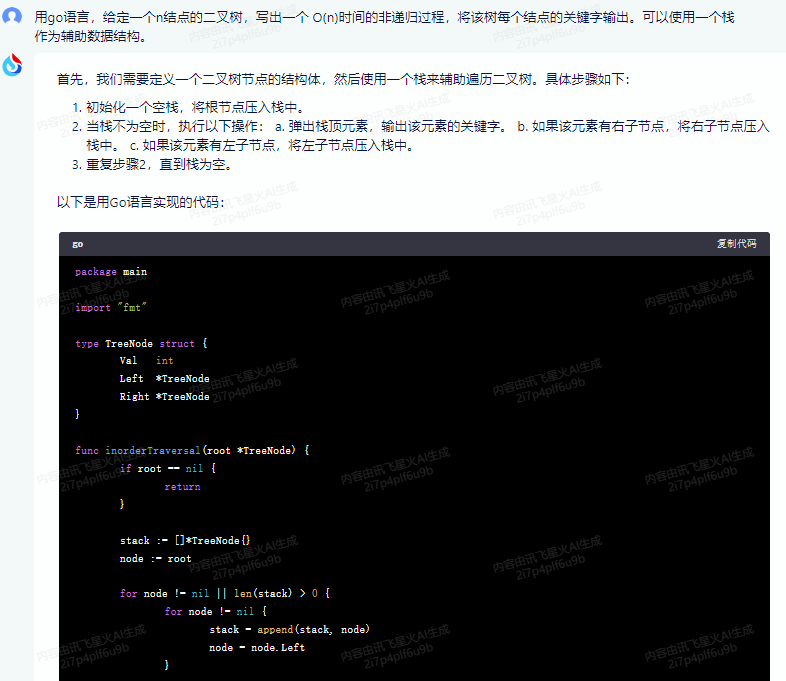
首先，我们需要定义一个二叉树节点的结构体，然后使用一个栈来辅助遍历二叉树。具体步骤如下：

  1. 初始化一个空栈，将根节点压入栈中。
  2. 当栈不为空时，执行以下操作：
    a. 弹出栈顶元素，输出该元素的关键字。
    b. 如果该元素有右子节点，将右子节点压入栈中。
    c. 如果该元素有左子节点，将左子节点压入栈中。
  3. 重复步骤2，直到栈为空。

以下是用Go语言实现的代码：

package main

import "fmt"

type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

func inorderTraversal(root *TreeNode) {
	if root == nil {
		return
	}

	stack := []*TreeNode{}
	node := root

	for node != nil || len(stack) > 0 {
		for node != nil {
			stack = append(stack, node)
			node = node.Left
		}

		node = stack[len(stack)-1]
		stack = stack[:len(stack)-1]
		fmt.Println(node.Val)

		node = node.Right
	}
}

func main() {
	root := &TreeNode{Val: 1}
	root.Left = &TreeNode{Val: 2}
	root.Right = &TreeNode{Val: 3}
	root.Left.Left = &TreeNode{Val: 4}
	root.Left.Right = &TreeNode{Val: 5}
	root.Right.Left = &TreeNode{Val: 6}
	root.Right.Right = &TreeNode{Val: 7}

	inorderTraversal(root)
}

这段代码首先定义了一个二叉树节点的结构体TreeNode，然后实现了一个非递归的中序遍历函数inorderTraversal，最后在main函数中创建了一个示例二叉树并调用inorderTraversal函数进行遍历。

在这里插入图片描述

在这里插入图片描述

360智脑：

以下是一个使用栈的非递归遍历二叉树的方法，可以输出每个结点的关键字：

package main

import (
    "fmt"
)

type Node struct {
    data int
    left *Node
    right *Node
}

func printTree(root *Node) {
    if root == nil {
        return
    }

    stack := []int{root.data}
    for _, v := range stack {
        fmt.Printf("%d ", v)
    }

    node := stack[len(stack)-1]
    left := root.left
    right := root.right

    stack = []int{}
    for node != nil {
        stack = append(stack, node.data)
        node = node.left
    }

    fmt.Println()
}

func main() {
    root := &Node{data: 10, left: &Node{}, right: &Node{data: 20}}

    printTree(root)
}

该程序首先创建一个包含当前结点的值的数组，并使用一个循环将数组中的元素依次输出。然后，程序将当前结点存储在栈中，并使用另一个循环将当前结点的左子树和右子树的结点分别推入栈中。最后，程序再次输出数组，以完成遍历。

该方法的时间复杂度为O(n)，其中n是二叉树中的结点数，因为它只遍历了树的深度，而没有进行任何嵌套遍历。

在这里插入图片描述

在这里插入图片描述

智谱清言：

package main
import "fmt"
type Node struct {  
   Key   int  
   Left  *Node  
   Right *Node  
}
func levelOrder(root *Node) {  
   if root == nil {  
       return  
   }
   stack := make([]*Node, 0)  
   stack = append(stack, root)
   for len(stack) > 0 {  
       node := stack[len(stack)-1]  
       stack = stack[:len(stack)-1]
       fmt.Print(node.Key, " ")
       if node.Left != nil {  
           stack = append(stack, node.Left)  
       }
       if node.Right != nil {  
           stack = append(stack, node.Right)  
       }  
   }  
}
func main() {  
   root := &Node{Key: 1}  
   root.Left = &Node{Key: 2}  
   root.Right = &Node{Key: 3}  
   root.Left.Left = &Node{Key: 4}  
   root.Left.Right = &Node{Key: 5}  
   root.Right.Right = &Node{Key: 6}
   levelOrder(root)  
}

这个程序首先定义了一个 Node 结构体，用于存储二叉树节点的关键字、左子节点和右子节点。然后，我们实现了一个 levelOrder 函数，它接受一个二叉树的根节点作为参数。

在 levelOrder 函数中，我们使用一个栈作为辅助数据结构。我们首先将根节点压入栈中，然后遍历栈。对于每个节点，我们首先输出它的关键字，然后将它的左右子节点依次压入栈中。当栈为空时，遍历结束。

在 main 函数中，我们创建了一个简单的二叉树，并调用 levelOrder 函数输出每个节点的关键字。输出结果为：1 2 4 5 3 6。

在这里插入图片描述

在这里插入图片描述

通义千问：

下面是一个Go语言实现的例子：

package main

import (
	"fmt"
)

type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

func levelOrder(root *TreeNode) [][]int {
	if root == nil {
		return nil
	}
	var res [][]int
	stack := []*TreeNode{root}
	for len(stack) > 0 {
		tmp := stack
		stack = nil
		row := []int{}
		for _, node := range tmp {
			row = append(row, node.Val)
			if node.Left != nil {
				stack = append(stack, node.Left)
			}
			if node.Right != nil {
				stack = append(stack, node.Right)
			}
		}
		res = append(res, row)
	}
	return res
}

func printTree(root *TreeNode) {
	for i := 0; i < len(levelOrder(root)); i++ {
		fmt.Println(levelOrder(root)[i])
	}
}

func main() {
	root := &TreeNode{1, &TreeNode{2, nil, nil}, &TreeNode{3, nil, nil}}
	printTree(root)
}

在这个例子中，我们首先定义了一个二叉树节点的结构体TreeNode，然后定义了一个函数levelOrder用于获取二叉树的层序遍历结果，最后定义了函数printTree用于打印二叉树的所有节点。

在levelOrder函数中，我们使用了一个栈来辅助遍历。首先我们将根节点放入栈中，然后进入循环，每次从栈中取出一个节点，将其值添加到当前行，然后将其左右子节点（如果存在）放入栈中。这样就可以保证每行都是同一层的节点。当栈为空时，说明所有节点都已经处理完毕，此时返回当前行的结果。

在printTree函数中，我们只需要调用levelOrder函数获取所有的层序遍历结果，然后逐行打印即可。

在这里插入图片描述

在这里插入图片描述

天工：

以下是使用 Go 语言实现 O(n) 时间复杂度的非递归方式遍历二叉树的代码：

type TreeNode struct {
    Val int
    Left *TreeNode
    Right *TreeNode
}

func printTree(root *TreeNode) {
    if root == nil {
        return
    }
    // 创建一个栈
    stack := make([]*TreeNode, 0)
    // 将根节点入栈
    stack = append(stack, root)
    // 循环直到栈为空
    for len(stack) > 0 {
        // 弹出栈顶节点
        node := stack[len(stack)-1]
        stack = stack[:len(stack)-1]
        // 如果节点有右子树，将其入栈
        if node.Right != nil {
            stack = append(stack, node.Right)
        }
        // 如果节点有左子树，将其入栈
        if node.Left != nil {
            stack = append(stack, node.Left)
        }
        // 输出节点的值
        fmt.Println(node.Val)
    }
}

在上述代码中，我们首先判断根节点是否为空，如果为空，则直接返回。接着，我们创建一个栈，并将根节点入栈。然后，我们循环直到栈为空。

在每次循环中，我们从栈中弹出栈顶节点，并判断该节点是否有右子树和左子树。如果该节点有右子树，则将其入栈；如果该节点有左子树，则将其入栈。最后，我们输出该节点的值。

通过这种方式，我们可以在 O(n) 时间复杂度内遍历二叉树，并输出每个节点的关键字。

在这里插入图片描述

在这里插入图片描述

chatgpt：

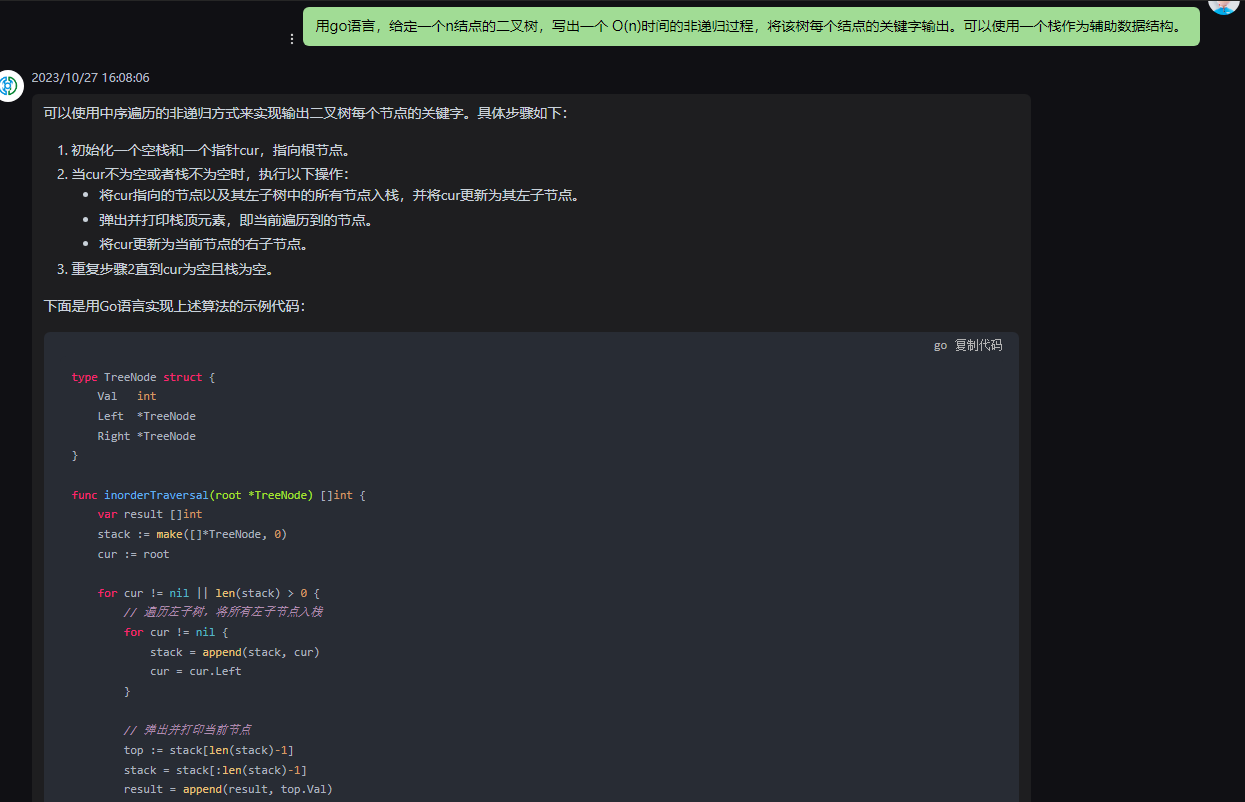
可以使用中序遍历的非递归方式来实现输出二叉树每个节点的关键字。具体步骤如下：

  1. 初始化一个空栈和一个指针cur，指向根节点。
  2. 当cur不为空或者栈不为空时，执行以下操作：
    • 将cur指向的节点以及其左子树中的所有节点入栈，并将cur更新为其左子节点。
    • 弹出并打印栈顶元素，即当前遍历到的节点。
    • 将cur更新为当前节点的右子节点。
  3. 重复步骤2直到cur为空且栈为空。

下面是用Go语言实现上述算法的示例代码：

type TreeNode struct {
    Val   int
    Left  *TreeNode
    Right *TreeNode
}

func inorderTraversal(root *TreeNode) []int {
    var result []int
    stack := make([]*TreeNode, 0)
    cur := root
    
    for cur != nil || len(stack) > 0 {
        // 遍历左子树，将所有左子节点入栈
        for cur != nil {
            stack = append(stack, cur)
            cur = cur.Left
        }
        
        // 弹出并打印当前节点
        top := stack[len(stack)-1]
        stack = stack[:len(stack)-1]
        result = append(result, top.Val)
        
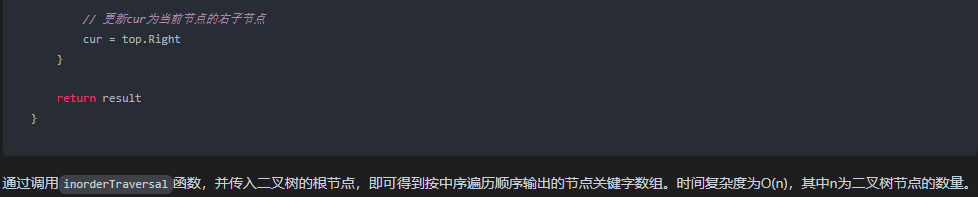
        // 更新cur为当前节点的右子节点
        cur = top.Right
    }
    
    return result
}

通过调用inorderTraversal函数，并传入二叉树的根节点，即可得到按中序遍历顺序输出的节点关键字数组。时间复杂度为O(n)，其中n为二叉树节点的数量。

在这里插入图片描述

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1143951.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Web应用系统设计

Web应用系统设计

Web应用设计的本质目的是为了解决软件系统的复杂性，所以我们在进行web设计时，首先要分析系统的复杂性，然后再进行设计。 1.案例 某公司在创业初期快速地开发了一个B2C的垂直电商网站，然后就迅速的投向市场进行运营。为了能够快速上线，系统设计得非常简单，选择了三层架构…
阅读更多...
大厂面试题-Java并发编程基础篇（一）

大厂面试题-Java并发编程基础篇（一）

目录 一、什么是守护线程&#xff0c;它有什么特点 二、谈谈你对AQS的理解 三、AbstractQueuedSynchronized为什么采用双向链表 四、lock和synchronized区别 五、线程池如何知道一个线程的任务已经执行完成 六、什么叫做阻塞队列的有界和无界 七、ConcurrentHashMap底层…
阅读更多...
拓扑排序基础详解，附有练习题

拓扑排序基础详解，附有练习题

介绍 拓扑排序是一种对有向无环图&#xff08;DAG&#xff09;进行排序的算法。在一个有向图中&#xff0c;如果存在一条从节点 A 到节点 B 的路径&#xff0c;那么节点 A 就依赖于节点 B。 有向无环图如下 什么是入度&#xff0c;出度&#xff1f; 入度&#xff1a;有多少个…
阅读更多...
10款轻量型的嵌入式GUI库分享

10款轻量型的嵌入式GUI库分享

LVGL LittlevGL是一个免费的开源图形库&#xff0c;提供了创建嵌入式GUI所需的一切&#xff0c;具有易于使用的图形元素、漂亮的视觉效果和低内存占用。 特点&#xff1a; 强大的构建模组 按钮、图表、列表、滑块、图像等 ​先进的图形 动画、反锯齿、半透明、平滑滚动 多样…
阅读更多...
【VR开发】【Unity】【VRTK】1-无代码VRVR开发介绍

【VR开发】【Unity】【VRTK】1-无代码VRVR开发介绍

本篇开始精简讲解VRTK相关的知识。 VRTK是基于Unity的一套提供无代码VR开发的插件，这套插件开源，可商用，集合了目前可能的VR体验组件，可以让不会C#编程但想要开发VR体验的人在不写一行代码的前提下开发出心仪的VR作品。 这套组件问世后也很受欢迎，目前已经进化到了第四代…
阅读更多...
2023阿里云双十一优惠活动「云上聚·创未来」价格和代金券领取

2023阿里云双十一优惠活动「云上聚·创未来」价格和代金券领取

2023阿里云双十一优惠活动「金秋云创季」开始啦&#xff0c;10月27日到10月31日可以领满减优惠&#xff0c;到11月1日和11月11日之间可以购买云服务器等产品&#xff0c;11.12到11.30日赢最高百万上云抵扣金&#xff0c;阿里云百科aliyunbaike.com分享2023阿里云双十一优惠活动…
阅读更多...
合成数据的好处和用途

合成数据的好处和用途

在不断变化的数据科学和人工智能环境中&#xff0c;合成数据集的概念成为具有多种用途的强大工具。 假设您是一名数据科学家&#xff0c;并分配了为电子商务网站创建尖端推荐系统的任务。为此&#xff0c;您需要大量的用户交互数据。但是&#xff0c;您面临着保护用户隐私和处…
阅读更多...
基本微信小程序的外卖点餐订餐平台

基本微信小程序的外卖点餐订餐平台

项目介绍 餐饮行业是一个传统的行业。根据当前发展现状&#xff0c;网络信息时代的全面普及&#xff0c;餐饮行业也在发生着变化&#xff0c;单就点餐这一方面&#xff0c;利用手机点单正在逐步进入人们的生活。传统的点餐方式&#xff0c;不仅会耗费大量的人力、时间&#xf…
阅读更多...
世界前沿技术发展报告2023《世界航空技术发展报告》（三）民用飞机技术

世界前沿技术发展报告2023《世界航空技术发展报告》（三）民用飞机技术

&#xff08;三&#xff09;民用飞机技术 1.干线飞机1.1 中国C919客机获得型号合格证并交付使用1.2 空客公司A321XLR超远程型窄体客机完成首飞1.3 NASA持续开展下一代民机技术研究1.4 欧洲开展“超高性能机翼”演示验证项目 2.支线飞机2.1 德国航宇中心完成“电动飞机概念及技术…
阅读更多...
世界前沿技术发展报告2023《世界航空技术发展报告》（四）无人机技术

世界前沿技术发展报告2023《世界航空技术发展报告》（四）无人机技术

&#xff08;四&#xff09;无人机技术 1.无人作战飞机1.1 美国空军披露可与下一代战斗机编组作战的协同式无人作战飞机项目1.2 俄罗斯无人作战飞机取得重要进展 2.支援保障无人机2.1 欧洲无人机项目通过首个里程碑2.2 美国海军继续开展MQ-25无人加油机测试工作 3.微小型无人机…
阅读更多...
Python+pytest+request 接口自动化测试！

Python+pytest+request 接口自动化测试！

一、环境配置 1.安装python3 brew update brew install pyenv 然后在 .bash_profile 文件中添加 eval “$(pyenv init -)” pyenv install 3.5.3 -v pyenv rehash 安装完成后&#xff0c;更新数据库 pyenv versions 查看目前系统已安装的 Python 版本 pyenv global 3.5…
阅读更多...
C#WinformListView实现缺陷图片浏览器

C#WinformListView实现缺陷图片浏览器

C#&Winform&ListView实现缺陷图片浏览器 功能需求图像浏览行间距调整悬浮提示 功能需求 机器视觉检测系统中特别是缺陷检测系统&#xff0c;通常需要进行对已经检出的缺陷图片进行浏览查阅。主要是通过条件筛选查询出所需要的数据&#xff0c;进行分页再展示到界面中。…
阅读更多...
基于SpringBoot的垃圾分类管理系统

基于SpringBoot的垃圾分类管理系统

基于SpringBootVue的垃圾分类管理系统的设计与实现~ 开发语言&#xff1a;Java数据库&#xff1a;MySQL技术&#xff1a;SpringBootMyBatis工具&#xff1a;IDEA/Ecilpse、Navicat、Maven主要功能&#xff1a;包括前台和后台两部分、首页列表展示、垃圾分类、垃圾图谱、查看详…
阅读更多...
当线性规划与算法相遇：揭秘单纯形法（Simplex）的独特魅力

当线性规划与算法相遇：揭秘单纯形法（Simplex）的独特魅力

传统的解决线性规划问题的方法是图形法、代数法求解&#xff0c;但是图形法解题有极大的局限性&#xff0c;因为一旦变量超过3个&#xff0c;基本上就无法通过图形解决&#xff0c;而代数法虽然可以解题&#xff0c;但对于复杂的问题可能效果较差甚至无法求解&#xff01; 相比…
阅读更多...
嵌入式PID算法理论+实践分析

嵌入式PID算法理论+实践分析

1.1 概述 比例&#xff08;Proportion&#xff09;积分&#xff08;Integral&#xff09;微分&#xff08;Differential&#xff09;控制器&#xff08;PID控制器或三项控制器&#xff09;是一种采用反馈的控制回路机制&#xff0c;广泛应用于工业控制系统和需要连续调制控制的…
阅读更多...
LangChain+LLM实战---LangChain概述

LangChain+LLM实战---LangChain概述

LangChain介绍 LangChain是个开源的框架&#xff0c;它可以让AI开发人员把像GPT-4这样的大型语言模型(LLM)和外部数据结合起来。可以简单认为LangChain是LLM领域的Spring&#xff0c;以及开源版的ChatGPT插件系统。 LangChain的强大之处不仅能通过API调用语言模型&#xff0c;…
阅读更多...
LLMs之ChatGLM3：ChatGLM3/ChatGLM3-6B的简介(多阶段增强+多模态理解+AgentTuning技术)、安装、使用方法之详细攻略

LLMs之ChatGLM3：ChatGLM3/ChatGLM3-6B的简介(多阶段增强+多模态理解+AgentTuning技术)、安装、使用方法之详细攻略

LLMs之ChatGLM3&#xff1a;ChatGLM3/ChatGLM3-6B的简介(多阶段增强多模态理解AgentTuning技术)、安装、使用方法之详细攻略 导读&#xff1a;2023年10月27日&#xff0c;智谱AI在2023中国计算机大会上推出了全自研的第三代基座大模型ChatGLM3及其相关系列产品&#xff0c;这是…
阅读更多...
系列二十一、请描述BeanDefinition的加载过程

系列二十一、请描述BeanDefinition的加载过程

一、概述 BeanDefinition是用来描述bean的生产信息&#xff0c;决定bean如何生产&#xff0c;是一个定义态的bean。 二、流程 2.1、第一步&#xff1a;启动IOC容器 AnnotationConfigApplicationContext context new AnnotationConfigApplicationContext(MySpringConfig.cla…
阅读更多...
嵌入式系统中C++ 类的设计和实现分析

嵌入式系统中C++ 类的设计和实现分析

C代码提供了足够的灵活性&#xff0c;因此对于大部分工程师来说都很难把握。 本文介绍了写好C代码需要遵循的10个最佳实践&#xff0c;并在最后提供了一个工具可以帮助我们分析C代码的健壮度。 原文&#xff1a;10 Best practices to design and implement a C class。 1. 尽…
阅读更多...
基于回溯搜索算法的无人机航迹规划-附代码

基于回溯搜索算法的无人机航迹规划-附代码

基于回溯搜索算法的无人机航迹规划 文章目录 基于回溯搜索算法的无人机航迹规划1.回溯搜索搜索算法2.无人机飞行环境建模3.无人机航迹规划建模4.实验结果4.1地图创建4.2 航迹规划 5.参考文献6.Matlab代码 摘要&#xff1a;本文主要介绍利用回溯搜索算法来优化无人机航迹规划。 …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023