本文属于「征服LeetCode」系列文章之一，这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁，本系列将至少持续到刷完所有无锁题之日为止；由于LeetCode还在不断地创建新题，本系列的终止日期可能是永远。在这一系列刷题文章中，我不仅会讲解多种解题思路及其优化，还会用多种编程语言实现题解，涉及到通用解法时更将归纳总结出相应的算法模板。

为了方便在PC上运行调试、分享代码文件，我还建立了相关的仓库：https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中，你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等，还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解，还可以一同分享给他人。

由于本系列文章的内容随时可能发生更新变动，欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。

矩形蛋糕的高度为 h 且宽度为 w，给你两个整数数组 horizontalCuts 和 verticalCuts，其中：

• horizontalCuts[i] 是从矩形蛋糕顶部到第  i 个水平切口的距离
• verticalCuts[j] 是从矩形蛋糕的左侧到第 j 个竖直切口的距离

请你按数组 horizontalCuts 和 verticalCuts 中提供的水平和竖直位置切割后，请你找出 面积最大 的那份蛋糕，并返回其 面积 。由于答案可能是一个很大的数字，因此需要将结果 对 109 + 7 取余 后返回。

示例 1：

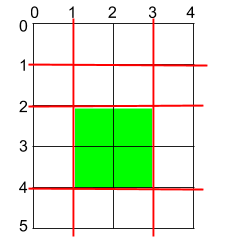
输入：h = 5, w = 4, horizontalCuts = [1,2,4], verticalCuts = [1,3]
输出：4 
解释：上图所示的矩阵蛋糕中，红色线表示水平和竖直方向上的切口。切割蛋糕后，绿色的那份蛋糕面积最大。

示例 2：

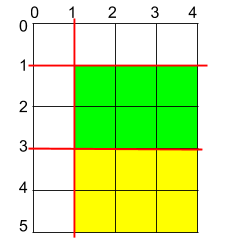
输入：h = 5, w = 4, horizontalCuts = [3,1], verticalCuts = [1]
输出：6
解释：上图所示的矩阵蛋糕中，红色线表示水平和竖直方向上的切口。切割蛋糕后，绿色和黄色的两份蛋糕面积最大。

示例 3：

输入：h = 5, w = 4, horizontalCuts = [3], verticalCuts = [3]
输出：9

提示：

• 2 <= h, w <= 10^9
• 1 <= horizontalCuts.length <= min(h - 1, 10^5)
• 1 <= verticalCuts.length <= min(w - 1, 10^5)
• 1 <= horizontalCuts[i] < h
• 1 <= verticalCuts[i] < w
• 题目数据保证 horizontalCuts 中的所有元素各不相同
• 题目数据保证 verticalCuts 中的所有元素各不相同

---

解法 贪心+排序

为了算出两个相邻切口的距离，把 $\text{horizontalCuts}$ 和 $\text{verticalCuts}$ 从小到大排序。

排序后，任意蛋糕都可以由两个相邻的水平切口和两个相邻的竖直切口决定（边界也算切口）。例如示例 1，水平切口 $2,4$ 和竖直切口 $1,3$ 就决定了面积最大的那份蛋糕。

所以蛋糕的面积可以表示为
$$(\text{horizontalCuts}[i]-\text{horizontalCuts}[i-1])\cdot (\text{verticalCuts}[j]-\text{verticalCuts}[j-1])$$
由于相乘的两项是互相独立的，只需要分别算出 $\text{horizontalCuts}[i]-\text{horizontalCuts}[i-1]$ 的最大值和 $\text{verticalCuts}[j]-\text{verticalCuts}[j-1]$ 的最大值，就得到了蛋糕面积的最大值。

也可以这样理解，先横着切，那么间隔最大的那两刀，就决定了最大的那条蛋糕，它包含着最终面积最大的那份蛋糕。接下来只需要知道竖着切时，两刀的最大间隔是多少，就知道了蛋糕的最大面积。

class Solution {
    int get_max_size(int size, vector<int> &cuts) {
        sort(cuts.begin(), cuts.end());
        int res = max(cuts[0], size - cuts.back());
        for (int i = 1; i < cuts.size(); i++) {
            res = max(res, cuts[i] - cuts[i - 1]);
        }
        return res;
    }
public:
    int maxArea(int h, int w, vector<int> &horizontalCuts, vector<int> &verticalCuts) {
        int max_h = get_max_size(h, horizontalCuts);
        int max_w = get_max_size(w, verticalCuts);
        return (long long) max_h * max_w % 1'000'000'007;
    }
};

复杂度分析：

• 时间复杂度：$\mathcal{O}(n\log n+m\log m)$ ，其中 $n$ 为 $\text{horizontalCuts}$ 的长度，$m$ 为 $\text{verticalCuts}$ 的长度。瓶颈在排序上。
• 空间复杂度：$\mathcal{O}(n)$ 或 $\mathcal{O}(1)$ 。