文章目录
- 前言
- 区间问题
- 判断区间是否重复
- 合并区间
- 插入区间
- 字符串分割
- 加油站问题
- 总结
前言
提示:如果生活把你的门关上了,那你就再打开,这就是门,门就是这样的。 --佚名
贪婪的思想不一定要理解的很透彻,但是贪婪的问题我们要掌握的很好,这里我们就研究一些高频的考察题目。
区间问题
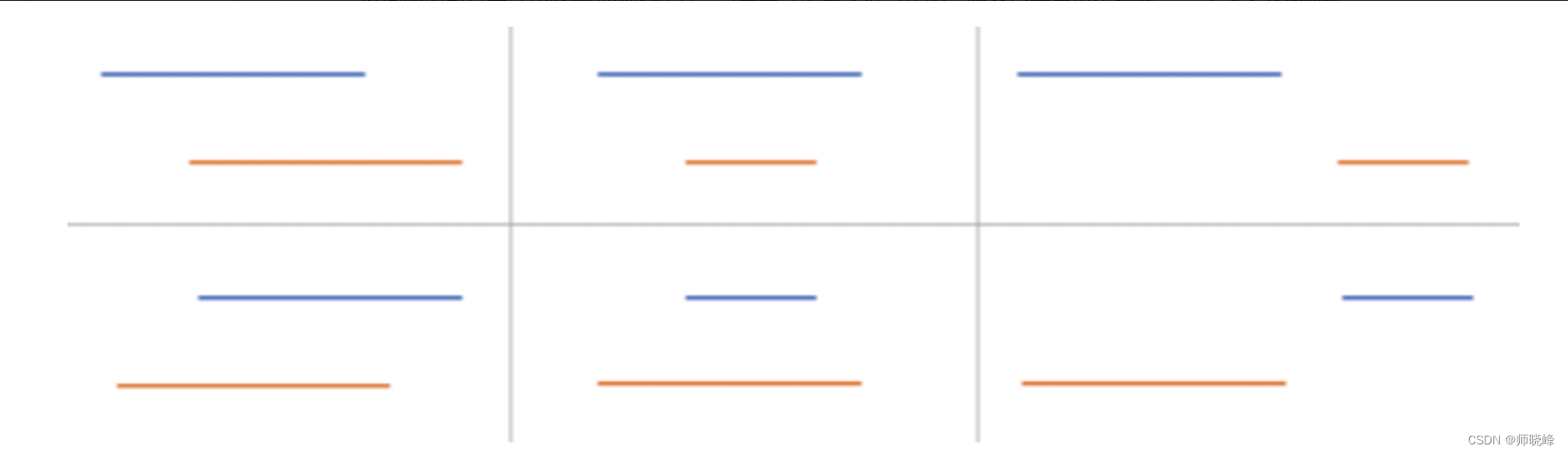
区间问题就是典型的面试中常见到的,这类面试题还是很受欢迎的,容易考察应聘者到底会不会写好代码。我们看看一些区间的例子🌰.两个区间的所有可能关系如下所示:
对于所有区间的问题,我们还是看看下面的图,一定要记住这些关系,很常见,也很容易出。
判断区间是否重复
参考地址连接:【leetcode】252 会议室(数组)_给定一个会议时间安排的数组-CSDN博客
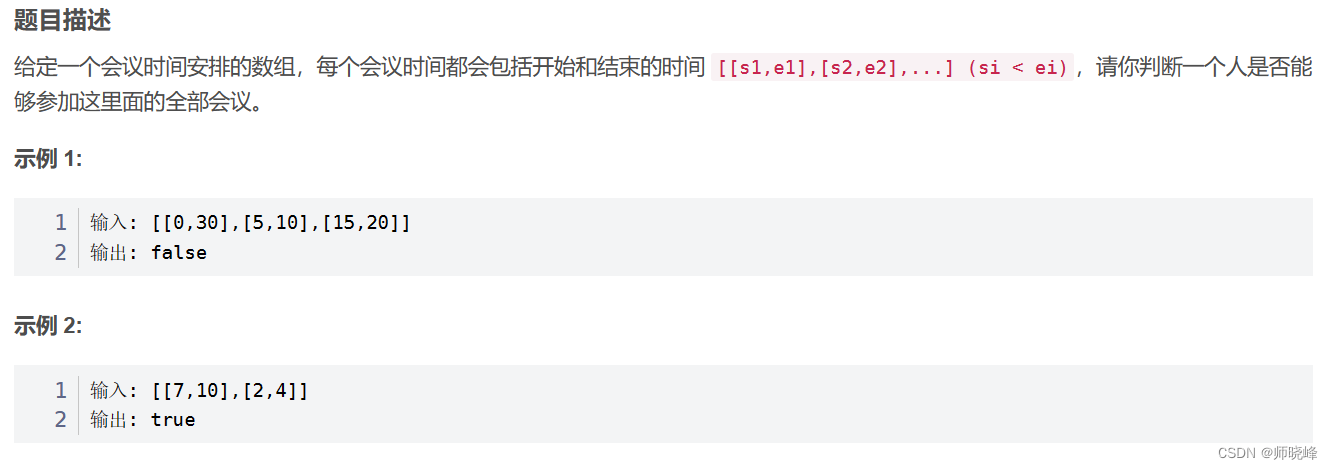
看下图🥰:
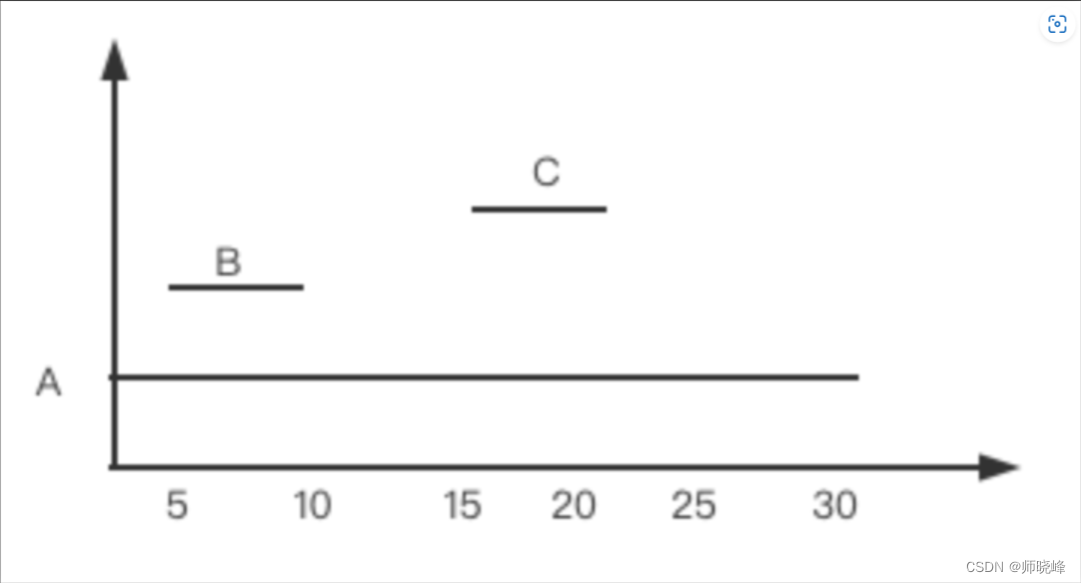
因为一个人同一时刻只能参加一个会议,因此题目实质是判断是否存在重叠区间的。将区间按照会议开始时间进行排序,然后遍历一遍判断后面的会议开始的时候是否前面的会议还没有结束即可,也就是上面的图中所显示的,如果存在重叠直接返回false即可。
/**
* 会议室(数组)
*
* @param intervals
* @return
*/
public static boolean canAttendMeetings(int[][] intervals) {
//将区间排序
Arrays.sort(intervals, (v1, v2) -> v1[0] - v2[0]);
// 遍历所有会议,是否出现重复 ( 技巧 从1 开始
for (int i = 1; i < intervals.length; i++) {
if (intervals[i][0] < intervals[i - 1][1]) {
return false;
}
}
return true;
}
合并区间
参考题目参数:56. 合并区间 - 力扣(LeetCode)


看下图🥰:
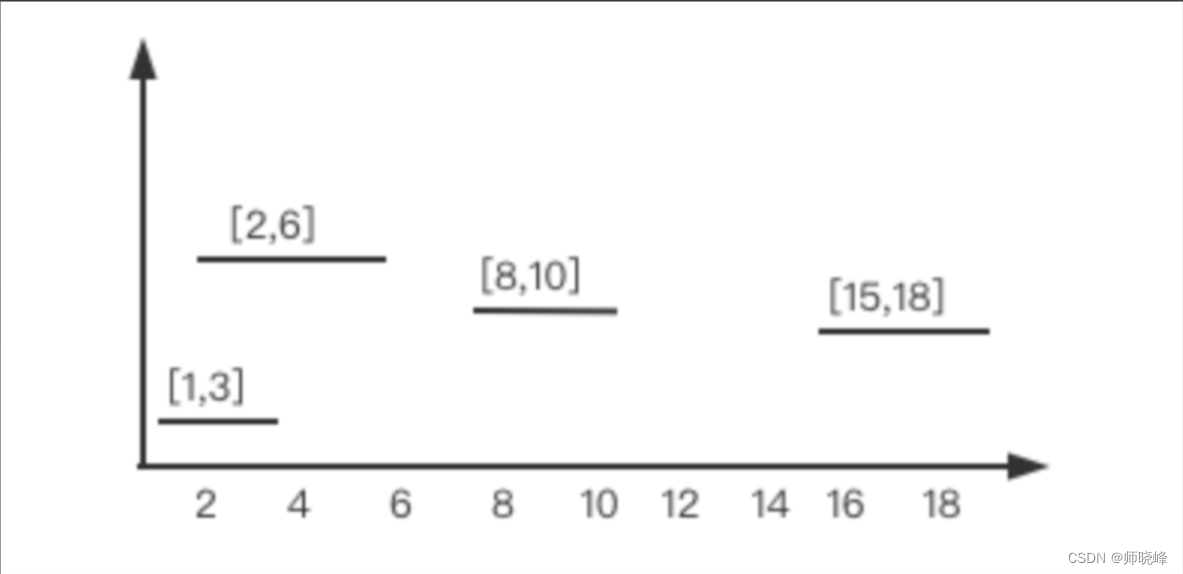
和上一题一样,首先对区间按照起点端点进行升序排序,然后逐个判断当前区间是否与前一个区间重叠,如果不重叠的话直接加入结果集,反之重叠的话(当前区间与前一个区间进行合并)
/**
* 合并区间
* @param intervals
* @return
*/
public static int[][] merge(int[][] intervals) {
// 排序数组
Arrays.sort(intervals,(v1,v2) ->v1[0] - v2[0]);
// 创建新的区间
int[][] merge = new int[intervals.length][2];
int idx = -1;
// 遍历数组
for(int [] interval: intervals){
// 如果数组是空的或者当前区间的起始位置 > 结果数组中最后区间的最大值
// 不合并区间,直接加入区间
if (idx == -1 && interval[0] > merge[idx][1]){
merge[++idx] = interval;
}else{
// 反之说明重叠,则将当前区间合并至结果数组的最后区间
merge[idx][1] = Math.max(merge[idx][1],interval[1]);
}
}
return Arrays.copyOf(merge, idx + 1);
}
插入区间
参考题目地址:57. 插入区间 - 力扣(LeetCode)
本题目也是上一个题目的扩展,这里区间已经按照起始结束升序排列了,我们可以直接遍历区间,寻找新区间的插入位置就可以了。
- 首先经新新区间左边且相离的区间加入结果集(遍历时,如果当前区间的结束位置,小于新区见的开始位置,说明当前区间在新区间的左边且相离)。
- 接着判断当前区间是否与新区间重叠,重叠的话就进行合并,知道遍历到当前区间在新区间的右边且相离,将最终合并后的新区间加入结果集;
- 最后将结果集右边且相离的区间加入结果集。
/**
* 插入区间
* @param intervals
* @param newInterval
* @return
*/
public static int[][] insert(int[][] intervals, int[] newInterval) {
// 创建一个足够大的数组
int[][] res = new int[intervals.length + 1][2];
int idx = 0;
// 左边的先进入(intervals[i][1] < newInterval[0]
//(后面还用的到
int i = 0;
while(i < intervals.length && intervals[i][1] < newInterval[0] ){
res[++idx] = intervals[i++];
}
// 合并新区间
while(i < intervals.length && intervals[i][0] <= newInterval[1]){
// 最左端
newInterval[0] = Math.min(newInterval[0], intervals[i][0]);
// 最右端
newInterval[1] = Math.min(newInterval[1],intervals[i][0]);
i++;
}
// 将合并的区间放入结果集
res[idx++]= newInterval;
// 放入右边的,直接放入结果集
while(i < intervals.length){
res[idx++]= intervals[i++];
}
return Arrays.copyOf(res,idx);
}
字符串分割
参考题目地址:763. Partition Labels - 力扣(LeetCode)

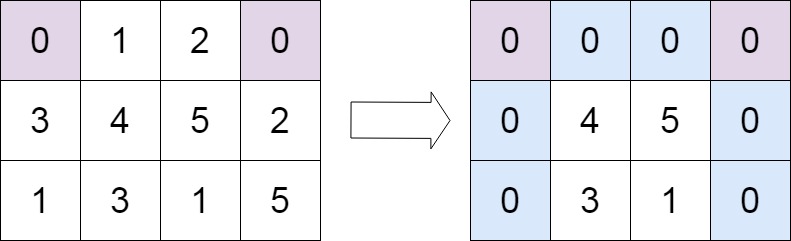
这个问题,有点回溯。分割问题是回溯算法的典型应用,但是这个问题如果用回溯将很复杂。题目要求同一个字母最多出现在一个片段中,那么要如何进行分片才算合理呢?🤔
该遍历过程相当于找每个字母的边界,如果知道之前遍历过的所有字母的最远边界,说明这个边界就是分割点了,此时前面出现的所有字母,最远也就到这个边界,所以做如下操作:
- 首先,统计每一个字符最后出现的位置
- 然后从头遍历字符,并更新字符的最远出现的下标,如果找到字符最远出现的下标和当前下标相等,则找到分割点。
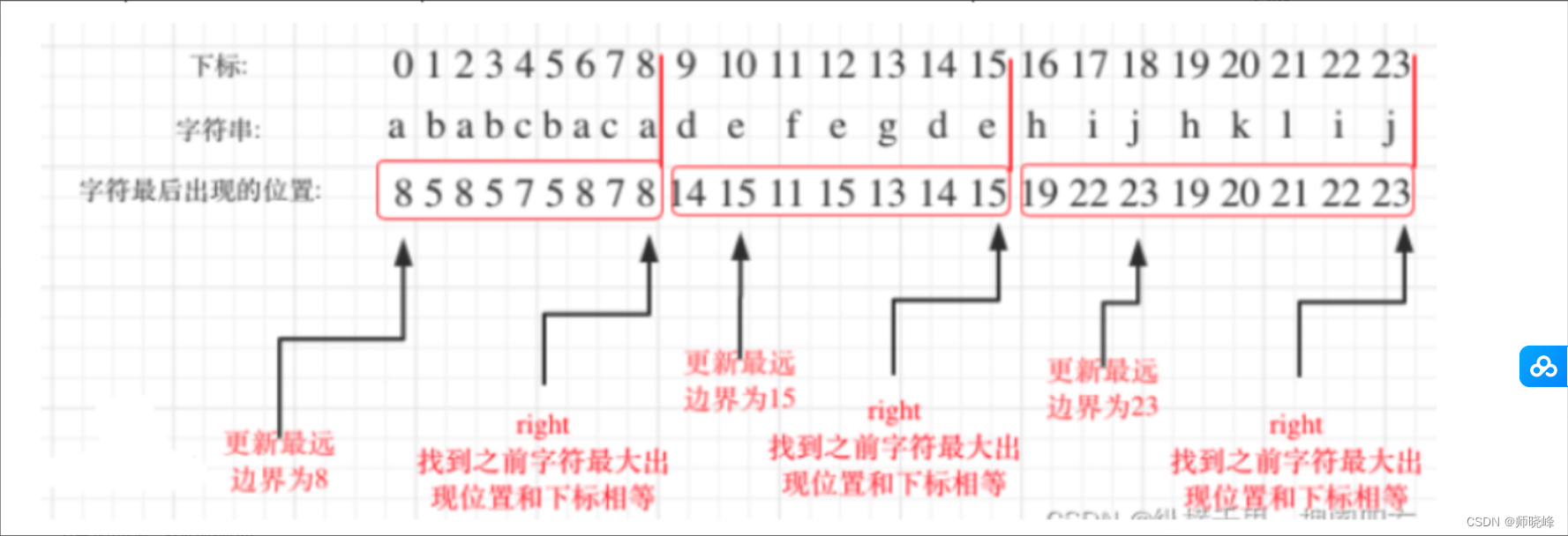
直接上代码:这个太神了
/**
* 划分字母区间
*
* @param S
* @return
*/
public static List<Integer> partitionLabels(String S) {
List<Integer> res = new ArrayList<Integer>();
int[] edge = new int[26];
char[] chars = S.toCharArray();
for (int i = 0; i < chars.length; i++) {
// 只保留最后一次的位置
edge[chars[i] - 'a'] = i;
}
int idx = 0;
int last = -1;
for (int i = 0; i < chars.length; i++) {
idx = Math.max(idx, edge[chars[i] - 'a']);
if (i == idx) {
// 这个非常巧妙
res.add(i - last);
last = i;
}
}
return res;
}
加油站问题
参考题目介绍:134. 加油站 - 力扣(LeetCode)


我们说做贪婪的题目,如果不管什么是贪婪,就直接做题。这里解释以下题目的含义:
实例给我们了两个数组,知识代表了当前站提供的油料,以及从前一个站过来需要消耗多少油料,因为是环,所以这里gas[0] = 1 和gas[0] = 3 就表示第一个站有1升汽油,从第一个站到第二个站需要消耗3升汽油.
当然最简单的方式是暴力从第一个试到最后一个。如图:
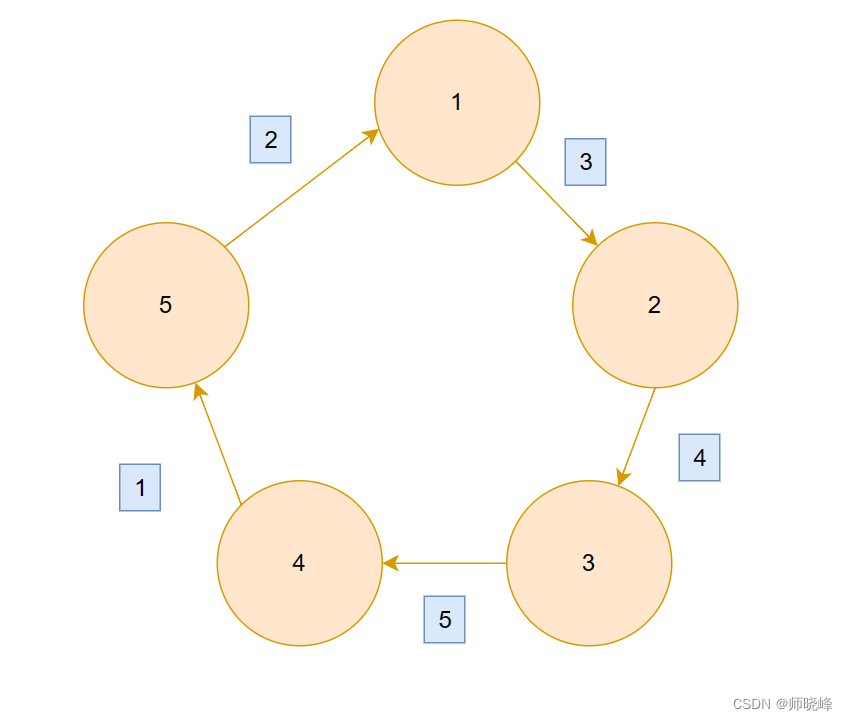
我们一直向后找,可以的话是一定有答案的。
但是,这个问题需要大量的重复计算,优化以下:
- 首先,如果总的油量大于(等于)总的消耗量,那么是可以跑完一圈的,具体就每段我们要考虑以下了。在具体一点是各个站的剩余油量rest[i]相加一点是大于等于零的。
- 每个加油站的剩余量rest[i]为gas[i] - cost[i].从i到0开始累加rest[i],和基座curSum,一旦curSum小于零,说明[0,i]区间都不能做起始位置,起始位置必须从i + 1开始重新算,只有这样才能保证我们有可能完成。
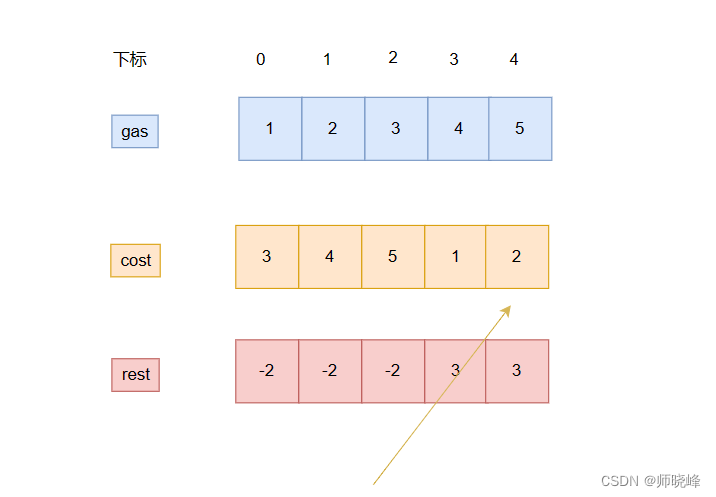
代码展示:
public int canCompleteCircuit(int[] gas, int[] cost) {
int start = 0;
int totalSum = 0;
int curSum = 0;
for(int i = 0; i < gas.length; i++){
curSum += gas[i] - cost[i];
totalSum += gas[i] - cost[i];
if(curSum < 0){
// 更新起始位置
start = i + 1;
// 更新curSum
curSum = 0;
}
}
// 说明不能走一圈
if(totalSum < 0){
return -1;
}
return start;
}
总结
提示:区间问题;字符串分割;加油站;贪婪算法;区间划分
如果有帮助到你,请给题解点个赞和收藏,让更多的人看到 ~ ("▔□▔)/
如有不理解的地方,欢迎你在评论区给我留言,我都会逐一回复 ~
也欢迎你 关注我 ,喜欢交朋友,喜欢一起探讨问题。