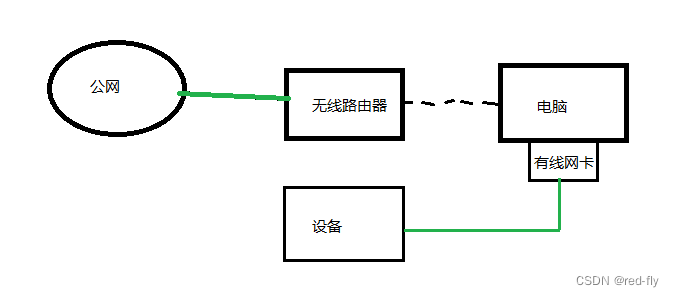
这一题是一个关于多次查询区间状态的一个问题，暴力肯定会超限，但是可以用莫队来优化暴力。

莫队的思想就是，用上一个区间的状态来更新当前区间的状态。

问题就是状态怎么更新以及求出当前区间的状态、也就是有多少对相同的袜子以及总共有多少袜子，通过这两个值可以求出来概率。

如何求出来有多少对相同的袜子，只需要遍历一遍当前区间记录每个颜色出现了多少次，当到了某个位置的时候，只需要知道之前的袜子有多少能跟自己配对即可。从区间中删除某个袜子也是如此，减去区间中跟自己颜色相同的袜子即可。

解释的不太好，看代码吧还是。

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define endl "\n"
//#define x first
//#define y second
#define int long long
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<int, string> pis;
typedef struct{
	int l, r, i;
}aa;
const int mod = 1e9 + 7;
const int N = 1e6+ 10;
int dx[] = {-1, 0, 1, 0, -1, 1, 1, -1};
int dy[] = {0, 1, 0, -1, 1, 1, -1, -1};
int n, m;
int o[N], f[N][2];
aa p[N];
int x, y;
int st[N], s;

inline void add(int a) // 加上当前位置
{
    // 首先需要知道之前一共有多少袜子颜色跟自己相同，就是当前袜子可以跟之前的组成多少对。
	s += st[o[a]] ++;
    // 加完之后把这个颜色的袜子加一
}
inline void del(int a) // 减去当前位置
{
    // 先是把当前的袜子从区间内减去，
    // 然后需要知道区间内一共有多少袜子颜色跟自己相同，就是当前袜子可以跟区间内的袜子组成多少对。
	s -= -- st[o[a]];
}
inline void query(int i, int l, int r) // 记录当前区间的概率， i表示是第i个问题，因为要按顺序输出
{
	if(s == 0)  // 特判不能组成袜子 
	{
		f[i][0] = 0, f[i][1] = 1;
		return ;
	}
	int k = r - l + 1; 
	k = k * (k - 1) / 2; // 这两行通过组合数求出不分颜色可以组成多少对袜子。
	int a = __gcd(k, s); // 化简为最简分数，需要计算出来最大公约数。
//	cout << s << " " << k << " " << a << endl;
	f[i][0] = s / a, f[i][1] = k / a; // 记录分子、分母。
}
int id[N];
inline void sovle()
{
	st[0] = 1;
	cin >> n >> m;
	int len = sqrt(n);
	for(int i = 1; i <= n; i ++)
	{
		cin >> o[i];
		id[i] = (i - 1) / len + 1;
	 } 
	for(int i = 0; i < m; i ++)
	{
		cin >> p[i].l >> p[i].r;
		p[i].i = i;
	}
	stable_sort(p, p + m, [&](aa a, aa b){  // 莫队特殊的排序方式
		if(id[a.l] == id[b.l]) 
		{
			if(id[a.l] & 1 == 1) return a.r < b.r;
			else return a.r > b.r;
		}
		else
		return id[a.l] < id[b.l];	
	});
	int l = 0, r = 0, k = 0;
	for(int i = 0; i < m; i ++) 
	{
		while(r > p[i].r) del(r --);
		while(r < p[i].r) add(++ r);
		while(l > p[i].l) add(-- l);
		while(l < p[i].l) del(l ++); // 这四部可以通过之前的区间移动到当前区间，在移动的过程中进行计算。
		query(p[i].i, p[i].l, p[i].r); // 记录当前区间的概率
	}
	for(int i = 0; i < m; i ++)
	{
		cout << f[i][0] << "/" << f[i][1] << endl;
	}
}

signed main(void)
{
	IOS;
	int t = 1;
//	cin >> t;
	while(t --) sovle();
	return 0;
}