夕小瑶科技说 原创
 作者 | 小戏

一旦谈及未来 AI，除了天马行空的科幻畅想，不可避免的也有未来 AI 时代的末日预言。从 AI 武器化到 AI 欺骗，从邪恶 AI 到 AI 掌权，人工智能，尤其是通用人工智能的风险始终都清清楚楚的写在人们的担忧之中。

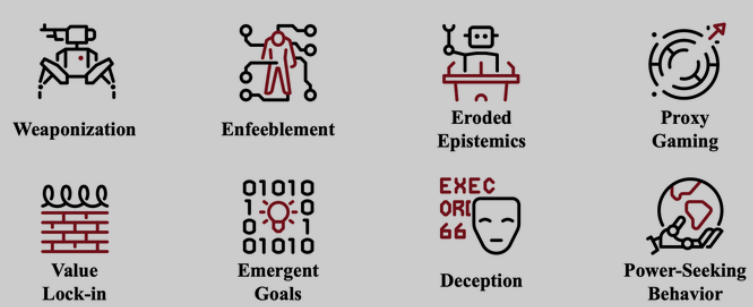
而伴随着以 GPT-4 为代表的大模型的出现，人类如何掌控这些拥有无法解释以致使用“涌现”而命名的神奇能力的大模型成为了一个巨大的灰犀牛问题，AI 的安全风险不会瞬间爆发，但是却不紧不慢的向我们奔袭而来。

而在昨天，OpenAI 在其安全与对齐社区中发布文章，宣布组建名为“Preparedness”的新团队，这个以“准备”甚至带着“战备”意味的词似乎表明 OpenAI 已经在试图为未来的 AI 风险付出认真的行动。

根据博客，OpenAI 表示自己已经开始积极的开展工作以应对 AI 相关的全方位的安全风险，这些风险不仅仅包含现在以 GPT 为基础架构的大模型潜在的风险，也包含未来可能的“超级人工智能”所蕴含的风险。具体而言，Preparedness 团队将评估与解决：

1. 在现在以及未来，前沿的 AI 系统被滥用，它们会有多危险？

2. 如何构建一个强大的框架来监控、评估、预测与防御前沿 AI 系统可能的风险？

3. 如果前沿的 AI 系统被盗用，恶意行为者可能会如何使用它们？

在这些大目标的基础上，这个由 MIT 教授 Aleksander Madry 领导的新团队将主要防范包括网络安全风险、化学风险、生物风险、辐射风险、核风险以及政治风险在内的多种灾难性风险。

此外，Preparedness 团队还将开发与维护一个风险指引发展策略（Risk-Informed Development Policy ，RDP），RDP 将详细阐释 OpenAI 将如何对自己开发的大模型进行风险监控，如何对大模型风险管理搭建治理体系与治理结构，以及如何对已发生风险进行补救。

▲image.png

与此同时，OpenAI 也发布了一个 AI 安全风险防范挑战赛用以预防 AI 被灾难性的滥用，挑战赛的 TOP 10 将获得总计 25000 美元的 API 积分。

挑战赛地址：
https://openai.com/form/preparedness-challenge

最后，组建新团队当然还有一步就是广发英雄帖：

▲image.png

目前在招的岗位有安全风险研究员以及研究工程师，怀揣拯救世界梦想的少年有没有去挑战 AI 这条恶龙的兴趣呢？