1、题目

2、题意

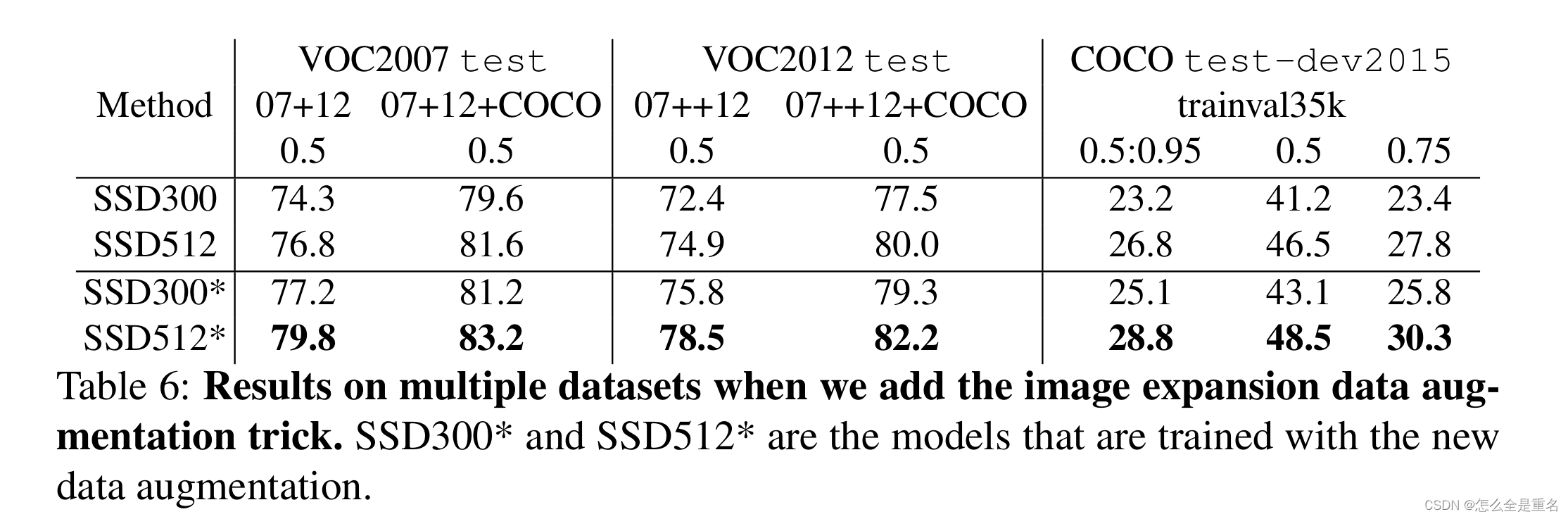
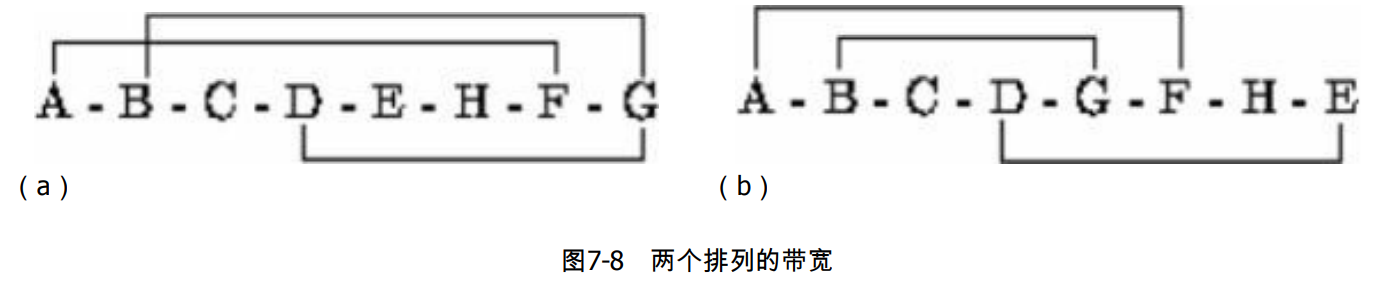
给出一个 $n（n\le 8）$个结点的图G和一个结点的排列，定义结点 $i$ 的带宽 $b(i)$ 为 $i$ 和相邻结点在排列中的最远距离，而所有 $b(i)$ 的最大值就是整个图的带宽。给定图G，求出让带宽最小的结点排列，如图所示。

下面两个排列的带宽分别为6和5。具体来说，图7-8（a）中各个结点的带宽分别为6, 6,1, 4, 1, 1, 6, 6，图7-8（b）中各个结点的带宽分别为5, 3, 1, 4, 3, 5, 1, 4。

3、分析

如果不考虑效率，本题可以递归枚举全排列，分别计算带宽，然后选取最小的一种方案。能否优化呢？和八皇后问题不同的是：八皇后问题有很多可行性约束（feasibility constraint），可以在得到完整解之前避免扩展那些不可行的结点，但本题并没有可行性约束——任何排列都是合法的。难道只能扩展所有结点吗？当然不是。

可以记录下目前已经找到的最小带宽 $k$。如果发现已经有某两个结点的距离大于或等于 $k$，再怎么扩展也不可能比当前解更优，应当强制把它“剪”掉，就像园丁在花园里为树修剪枝叶一样，也可以为解答树“剪枝（prune）”。

除此之外，还可以剪掉更多的枝叶。如果在搜索到结点 $u$ 时，$u$ 结点还有 $m$ 个相邻点没有确定位置，那么对于结点 $u$ 来说，最理想的情况就是这 $m$ 个结点紧跟在 $u$ 后面，这样的结点带宽为 $m$，而其他任何“非理想情况”的带宽至少为 $m+1$。这样，如果 $m\ge k$，即“在最理想的情况下都不能得到比当前最优解更好的方案”，则应当剪枝。

提示：在求最优解的问题中，应尽量考虑最优性剪枝。这往往需要记录下当前最优解，并且想办法“预测”一下从当前结点出发是否可以扩展到更好的方案。具体来说，先计算一下最理想情况可以得到怎样的解，如果连理想情况都无法得到比当前最优解更好的方案，则剪枝。

4、代码实现

#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;

const int maxn = 10;
int id[256], letter[maxn];

int main() {
	char input[1000];
  	while(scanf("%s", input) == 1 && input[0] != '#') {
    	// 计算结点个数并给字母编号
    	int n = 0;
    	for(char ch = 'A'; ch <= 'Z'; ch++)
      		if(strchr(input, ch) != NULL) {
        		id[ch] = n++;
        		letter[id[ch]] = ch;
      		}

		// 处理输入
    	int len = strlen(input), p = 0, q = 0;
    	vector<int> u, v;
   		for(;;) {
      		while(p < len && input[p] != ':') p++;
      		if(p == len) break;
      		while(q < len && input[q] != ';') q++;
      		for(int i = p+1; i < q; i++) {
        		u.push_back(id[input[p-1]]);
       			v.push_back(id[input[i]]);
      		}
      		p++; q++;
    	}

    	// 枚举全排列
    	int P[maxn], bestP[maxn], pos[maxn], ans = n;
    	for(int i = 0; i < n; i++) P[i] = i;
    	do {
			for(int i = 0; i < n; i++) pos[P[i]] = i; // 每个字母的位置
	      	int bandwidth = 0;
      		for(int i = 0; i < u.size(); i++)
        		bandwidth = max(bandwidth, abs(pos[u[i]] - pos[v[i]])); // 计算带宽
      		if(bandwidth < ans) {
        		ans = bandwidth;
        		memcpy(bestP, P, sizeof(P));
      		}
    	} while(next_permutation(P, P+n));

    	// 输出
    	for(int i = 0; i < n; i++) printf("%c ", letter[bestP[i]]);
    	printf("-> %d\n", ans);
  	}
  	return 0;
}