算术逻辑单元：

之前提过的运算器包括MQ,ACC,ALU,X,PSW；运算器可以实现运算以及一些辅助功能（移位，求补等）。

其中ALU负责运算，运算包括算术运算（加减乘除等）和逻辑运算（与或非，异或等）。ALU能同时处理的比特位数通常等于机器字长。

        逻辑运算：

与：  Y=A*B ;   类似于乘法，a和b要都为1，输入才能为1；

 或：  Y=A+B;   类似于加法，a和b有一个为1，输入就为1；

非：     Y=Ā;就是取反，a是0，y就是1，a是1，y就是0.

这里还有与或非的门电路，下面的图片。

在逻辑运算中，与 的优先级是大于 或的（与好比乘嘛，乘优先于加）。

逻辑运算也是符合分配律和结合律的，像这样a*（c+d）=ac+ad；（这个就是逻辑表达式）逻辑表达式本质上就是对电路的数学化描述，通过逻辑表达式可以构建出对于的电路，所以简化逻辑表达式实际上也就是在简化电路，还是钱的问题，简化省点钱。

这里在逻辑运算中实际上还有个反演律，可以看一下。

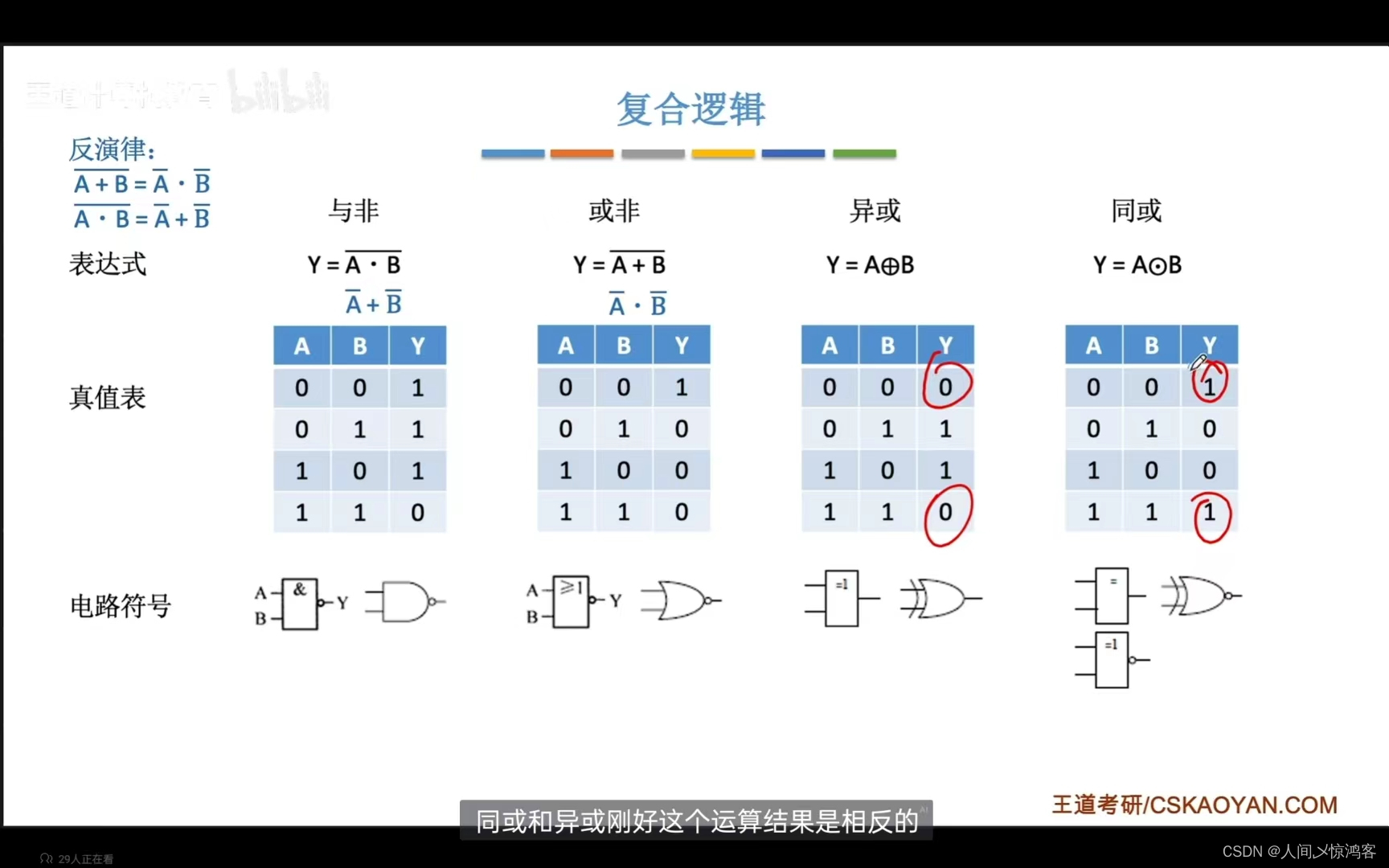        复合逻辑：

异或：异或就是相同为 0，不同为1.可以通过异或门电路来求偶校验位。

同或：同或的效果和异或的相反。

还有与非和或非，就是这两个逻辑的结合。

        一位全加器：

对于全加器，每次应该有三个输入（当前位的两个数值，来自低位的进位），两个输入（当前位求和的值（本位和），向高位的进位），哎，感觉这都蛮抽象的，用语言不太好描述。

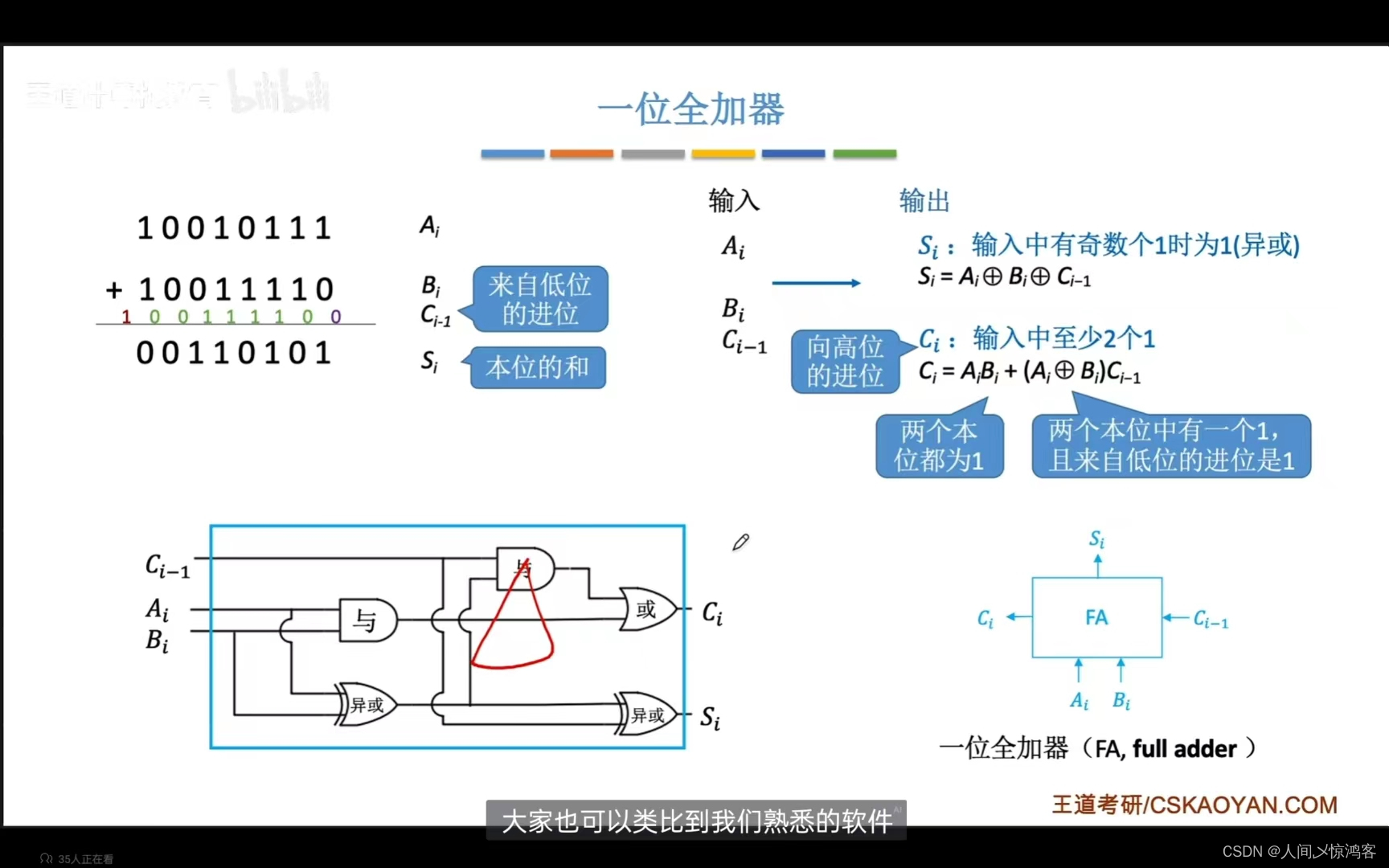
这里对于向高位的进位的实现还是挺有意思的。

然后还有一个串行加法器，其只有一个全加器，但比上面多了个进位触发器（用来保存进位数），数据逐位串行送入加法器中进行运算的时候，进位触发器用来寄存进位信号，以便参与下一次运算。这样的话，如果操作数长n位的话，加法就要分n次进行，每一位产生一位和，并且串行逐位地送回寄存器。

        并行加法器：

可以把多个全加器串接起来，每一个全加器处理一位的数据，这样可以进行两个n位数的相加，这样的叫做串行进位的并行加法器.

串行进位又称为行波进位，每一位进位直接依赖于前一位的进位，即进位信号是逐级形成的，这样实际上好像也并不能太多提升运算速度，因为还是要等前面的算完，才能轮到后面的。这里计算速度就主要取决于进位产生的速度，以及数据传递的速度。

        并行进位加法器

上面说了依赖低位来获得进位数据的话，会受到进位产生的速度和数据传递速度的影响，这里实际上实际上低位的进位数据，是通过低位运算产生的，那么可以直接通过向处理高位数据的全加器输入高位数据的同时，也输入低位数据，这样就是可以不等待低位的运算结果，而在一开始就进行运算，也就是说第 i 位向更高位的进位可以根据被加数，加数的第 1 ~ i 位，再结合最开始的进位来确定。

根据上面说的可以对并行加法器优化，实现的结果是并行进位的并行加法器，各级进位的信号同时形成，又称为先行进位，同时进位，但这里实际上对于高位来说和最初的那个一位加法器有点一样，从最低位开始算到当前位，可能比一位加法器好在不用反复的读取和输入数据了，一位加法器的每一位的运算结果是要传送到寄存器上的嘛，而这里目的只是当前的高位，过程中求的值无所谓。同时也要指出，随着位的增加，越高位的运算就会越复杂，后面得到结果也会越来越慢。

        补码加减运算其：

加法器的原理就是输入被加数和加数（被加数和加数比较长的话，大于机器字长，加法器一次运算是不够的），还有来自低位的进位，通过运算输出 最高位产生的进位和相加的结果，这里实际上还有其他的输出，就是标志位。

        补码加/减运算方法：

相加的话，直接按位相加就行；

相减的话，将减数的补码全部按位取反，末位加1（就是正变负，负变正，比如正变负吧，正的原码和补码一样，直接把补码当原码看，这个时候是正数的原码，把符号位取反 0 变 1，这个时候是这个数负数的原码，然后将这个负数的原码变成补码，操作就是符号位不变，其他位按位取反，然后在末位加1嘛，刚刚符号位由正变负的时候已经变过了，所以相当于全部位取反，然后加1.）

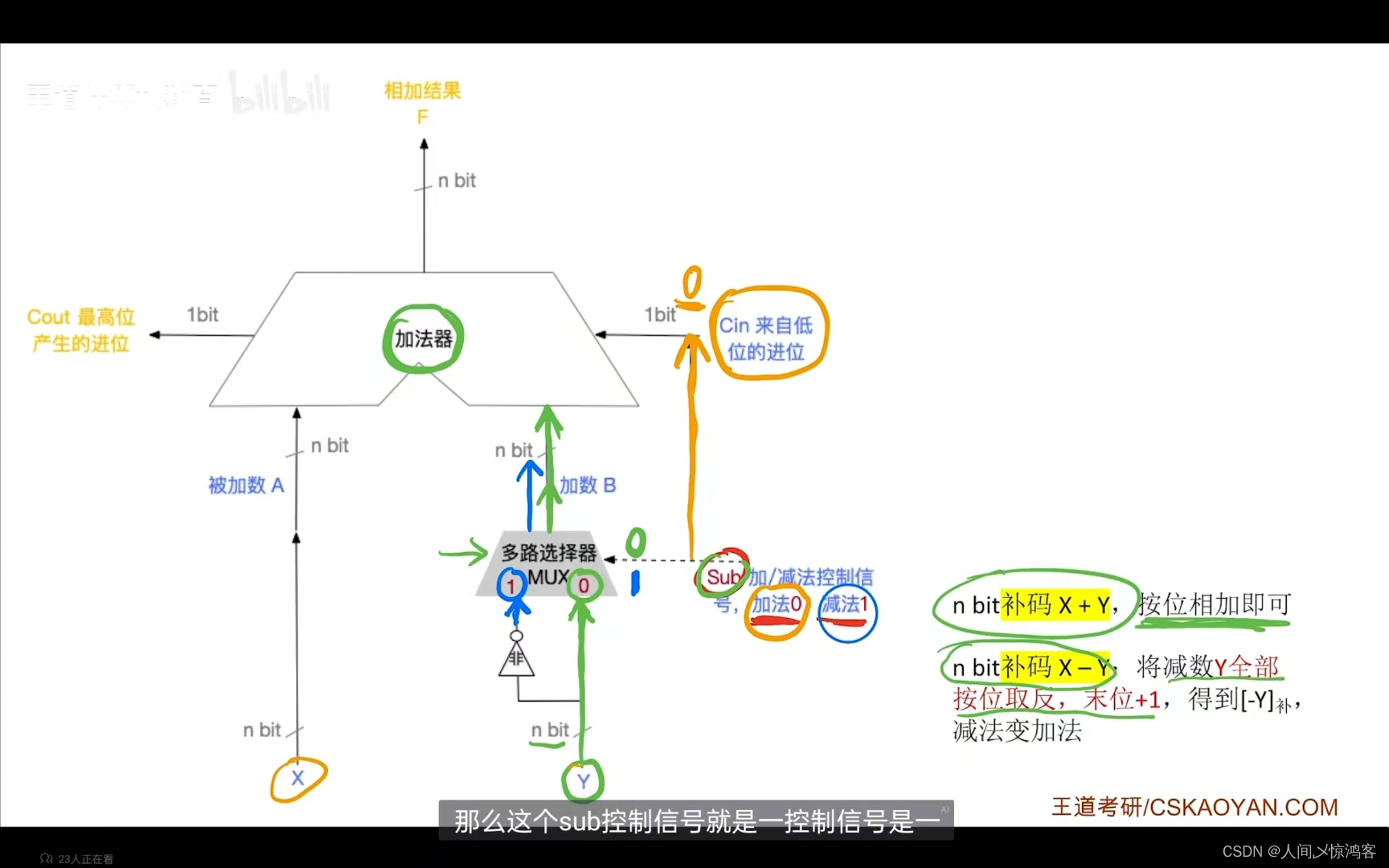
这个不好说，这个就是补码的加法器，它这里多了一个Sub加/减法控制信号，同时向选择器和低位的进位输入信息，如果是加法的话非门是关着的，低位的进位输入是 0 ，这样就都是补码直接参与运算，如果是减法的话，那非门就是打开的，另一边是关着的，这样的话就可以实现减数的全部为按位取反，而末位加一这个操作的实现是通过向低位的进位输入 1 来实现的，这里真的很巧妙，一个输入信号，即控制了加减，又实现了对数据处理，其实两个都是数据的处理，反正就是挺开眼的。

对于无符号整数的加法/减法也可以用该电路实现，其实无符号整数就可以理解为正数，能够处理正数，自然也可以处理无符号整数了。但是无符号整数也会有溢出的出现，注意。