目录
LeetCode之路——226. 翻转二叉树
分析
解法一:深度优先搜索
解法二:广度优先搜索
简单总结

LeetCode之路——226. 翻转二叉树
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:
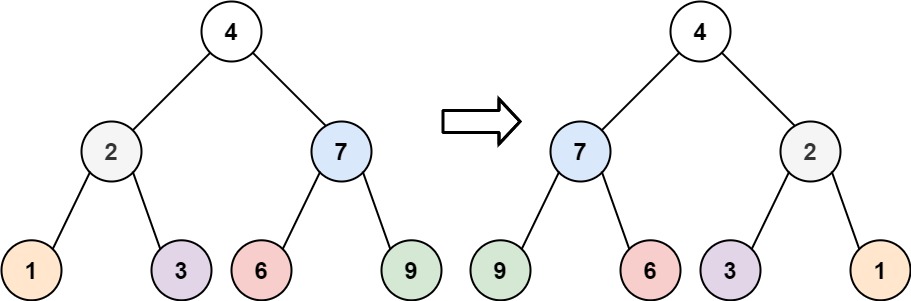
输入:root = [4,2,7,1,3,6,9] 输出:[4,7,2,9,6,3,1]
示例 2:
输入:root = [2,1,3] 输出:[2,3,1]
示例 3:
输入:root = [] 输出:[]
提示:
-
树中节点数目范围在
[0, 100]内 -
-100 <= Node.val <= 100
分析
简单题,关键点翻转二叉树就是交换左右子节点。
解法一:深度优先搜索
class Solution {
public TreeNode invertTree(TreeNode root) {
if (root == null) {
return null;
}
invertTree(root.left);
invertTree(root.right);
swap(root);
return root;
}
private void swap(TreeNode root) {
TreeNode tmp = root.left;
root.left = root.right;
root.right = tmp;
}
}
-
时间复杂度:O(n)
-
空间复杂度:O(n)
解法二:广度优先搜索
class Solution {
public TreeNode invertTree(TreeNode root) {
if (root == null) {return null;}
ArrayDeque<TreeNode> deque = new ArrayDeque<>();
deque.offer(root);
while (!deque.isEmpty()) {
int size = deque.size();
while (size-- > 0) {
TreeNode node = deque.poll();
swap(node);
if (node.left != null) deque.offer(node.left);
if (node.right != null) deque.offer(node.right);
}
}
return root;
}
public void swap(TreeNode root) {
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
}
}
-
时间复杂度:O(n)
-
空间复杂度:O(n)
简单总结
深度优先搜索(DFS)和广度优先搜索(BFS)是两种常用的二叉树遍历算法,它们在不同的情况下有不同的使用场景。
深度优先搜索(DFS):
-
前序遍历(Preorder Traversal):在前序遍历中,首先访问根节点,然后递归遍历左子树,最后递归遍历右子树。DFS前序遍历常用于复制整个二叉树的结构或生成树的深度优先遍历路径。
-
中序遍历(Inorder Traversal):在中序遍历中,首先递归遍历左子树,然后访问根节点,最后递归遍历右子树。中序遍历常用于获取有序的二叉搜索树中的元素。
-
后序遍历(Postorder Traversal):在后序遍历中,首先递归遍历左子树,然后递归遍历右子树,最后访问根节点。后序遍历常用于内存回收或树的结构修改等情况。
DFS的主要优点是它对于深度优先搜索路径的处理非常方便,因为它使用递归或栈来维护路径。在查找路径或在树中寻找特定元素时,DFS通常是有用的。
广度优先搜索(BFS):
-
层序遍历(Level Order Traversal):BFS按层级顺序遍历树,首先访问根节点,然后逐层遍历子节点。层序遍历非常适合用于寻找树的层级结构或找到最短路径等问题。
-
二叉树的宽度度量:BFS可用于测量二叉树的宽度,即树的某一层上的节点数。这在某些树结构的分析和问题求解中非常有用。
BFS的主要优点是它在许多情况下能够找到最短路径,因为它从根节点开始逐层扩展,直到找到目标节点。因此,BFS常用于寻找最短路径、解决迷宫问题、查找邻近节点等。