使用穷举法来解：

12个球分A1234、B1234、C1234

1、A1234=B1234→坏在C1234

1.1、A123=C123→坏在C4

1.2、A123<C123→坏在C123，且知坏的重

1.2.1、C1=C2→坏在C3

1.2.2、C1<C2→坏在C2

1.2.3、C1>C2→坏在C1

1.3、A123>C123→坏在C123，且知坏的轻

1.3.1、C1=C2→坏在C3

1.3.2、C1<C2→坏在C1

1.3.3、C1>C2→坏在C2

2、A1234<B1234→坏在A1234、B1234

2.1、A12B12=A3B3C12→坏在A4、B4，且知A4<B4

2.1.1、A1=A4→坏在B4，且由2知坏的重

2.1.2、A1<A4→A1<A4<B4，不可能出现

2.1.3、A1>A4→坏在A4，且由2知坏的轻

2.2、A12B12<A3B3C12→坏在A12、B3，且A12必有一个正常

2.2.1、A1=A2→坏在B3，且知坏的重

2.2.2、A1<A2→坏在A12，由2.2知坏的轻→坏在A1

2.2.3、A1>A2→坏在A12，由2.2知坏的轻→坏在A2

2.3、A12B12>A3B3C12→坏在A3、B12，且B12必有一个正常

2.3.1、B1=B2→坏在A3，且知坏的轻

2.3.2、B1<B2→坏在B12，由2.3知坏的重→坏在B2

2.3.3、B1>B2→坏在B12，由2.3知坏的重→坏在B1

3、A1234>B1234→坏在A1234、B1234

3.1、A12B12=A3B3C12→坏在A4、B4，且知A4>B4

3.1.1、A1=A4→坏在B4，且由3知坏的轻

3.1.2、A1<A4→坏在A4，且由3知坏的重

3.1.3、A1>A4→A1>A4>B4，不可能出现

3.2、A12B12<A3B3C12→坏在A3、B12，且B12必有一个正常

3.2.1、B1=B2→坏在A3，且知坏的重

3.2.2、B1<B2→坏在B12，且由3知坏的轻→坏在B1

3.2.3、B1>B2→坏在B12，且由3知坏的轻→坏在B2

3.3、A12B12>A3B3C12→坏在A12、B3，且A12必有一个正常

3.3.1、A1=A2→坏在B3，且知坏的轻

3.3.2、A1<A2→坏在A12，且由3知坏的重→坏在A2

3.3.3、A1>A2→坏在A12，且由3知坏的重→坏在A1

遗留问题：

我统计了球号出现的次数当做验证，直觉所有球号出现的次数应该是一样的

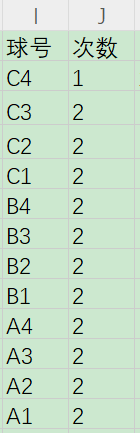
可是为什么C4出现的次数和其他的不一样（不管是1还是3）？

参考：

解题参考知乎-善兔的回答

图标参考百度百科-称球问题

软件测试笔试十大逻辑题，收藏这一篇就够了_软件开发笔试逻辑题大全及答案-CSDN博客