问题( 一 )
问题描述:
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序
题目链接:
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
问题分析:
提示:给定的数组是按从小到大的顺序排列的,可能大家容易想到的就是暴力破解,所有数先平方,简单粗暴。再进行排序。这里给大家讲的是双指针的思路。
例如给定的数组: nums={ -4 , -3 , 1 , 2 , 4}; 通过观察我们可以得出,平方之后两侧的数是最大的,所以双指针法,一个往右移动,一个向左移动,平方进行比较,大的存放到数组中,小的不移动,说明一点(这里我们放入数组的元素,是从尾部往前存放,这样得到得数组才是从小到大得顺序)。同时下面的代码中没有,对两个元素相等进行处理,为什么?1、 因为在实际处理的时候,遇到两个数相等的是比较少的 2、这样写的代码更简洁,可读性更高。
视频讲解(代码随想录):
双指针法经典题目 | LeetCode:977.有序数组的平方_哔哩哔哩_bilibili
解决方案:
vector<int> sortedSquares(vector<int>& nums) {
int left = 0 ;
int right = nums.size()-1;
vector< int> ret(right+1);
int num=right;
while( left < right ){
if( nums[left]*nums[left] < nums[right]*nums[right] ){
ret[num--]=nums[right]*nums[right];
right--;
}
else { //大于等于的情况
ret[num--]=nums[left]*nums[left];
left++;
}
}
ret[num]=nums[left]*nums[ left ];
return ret;
}问题( 二 )
问题描述:
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
题目链接:
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
问题分析:
求符合条件的数组,就是一个滑动窗口,其实也是双指针,前后两个指针固定住一个窗口。两个指针都指向数组的第一个元素,定义一个计数器(计算元素的值),第一个指针往后移动遍历元素,当我们的计数速器大于或者等于给定的 target 时,此时这个区间就是我们要找的子数组,此时我们的第一个指针往后移动,不断的压缩我们的窗口,取符合的最小窗口。
视频讲解:
双指针法经典题目 | LeetCode:977.有序数组的平方_哔哩哔哩_bilibili
解决方案:
int minSubArrayLen(int target, vector<int>& nums) {
int size=nums.size(); //记录子序列的长度
int sum=0 ; //子序列的元素的大小
int flag=0 ;
int lenth=0 ;
int i=0 ;
for(int j=0 ; j< nums.size() ; j++){
sum += nums[j];
while( sum >=target ){
lenth = j-i+1; //区间的长度
size= size > lenth ? lenth : size;
flag=1;
sum-=nums[i];
i++; //缩小区间长度
}
}
return flag ==1 ?size : 0 ;
}问题( 三 )
问题描述:
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
题目链接:
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
问题分析:
我们需要考虑转几圈,循环控制圈数。转圈的时候我们采用左闭右开的原则(大多数人可能会想不到这一点) 往左从零开始剩下一个元素没有处理,往下的时候就从剩下的这个元素开始,这样每处理一条边的时候,都会空出一个元素留给下一条边处理,转完一圈刚好全部点都处理完了,每次转圈的起始位置都在对角线的位置,此时我们还要考虑一个点如果圈速是奇数,说明中间是一个点,这里我们需要进行特殊处理。
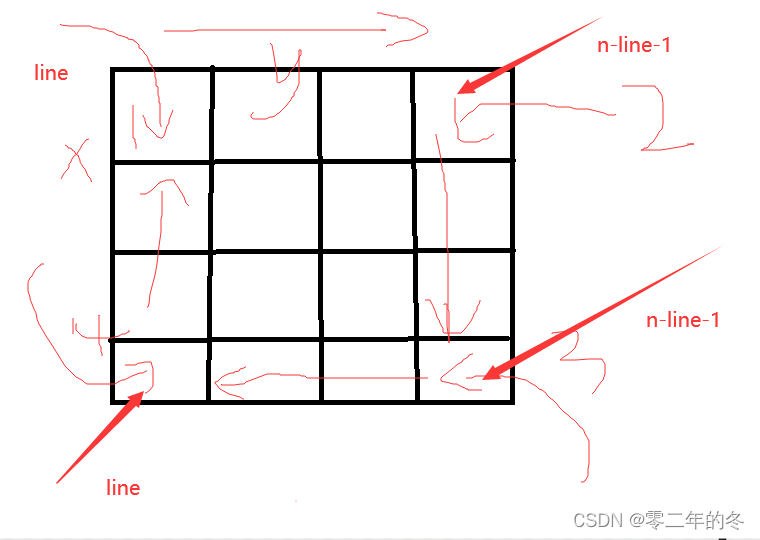
标注: 这里的 **line**用来更新我们每圈的起始位置,为什么要 n-line -1 ,因为每一条边的最后一个元素不出来,以及转完一圈后要缩小范围。
解决方案:
vector<vector<int>> generateMatrix(int n) {
int count=n/2 ; //要转的圈数
int x=0,y=0;
vector<vector<int>> ret(n,vector<int>(n,0)); //形成的矩阵
int value=1;
int line=0; //记录边界
while( count-- ){
// ->
for( x=line ; y < n-line-1 ; y++ ){
ret[x][y] = value++;
}
//往下
for( y=n-line-1 ; x < n-line-1 ; x++ ){
ret[x][y]=value++;
}
//往左
for( ; y > line ; y--){
ret[x][y]=value++;
}
//往上
for( ; x > line ; x--){
ret[x][y]=value++;
}
line++; //范围缩小
x += 1;
y += 1;
}
if(n%2!=0){ //说明中间留有一个位置
ret[x][y]=value;
}
return ret;
}