关于补码的文章，csdn上面遍地都是，所以我们大可不必搬运别人的文章来装点门面，我写这篇博客是想补充一个问题“补码为什么要+1”的问题，这个问题，博客园有个叫张子秋的文章写的很好，但是最后对补码为什么+1的问题，我想补充得更充分一点。

我们知道，在计算机里面

正整数：补码=反码=原码

[+1] = [0000 0001]原 = [0000 0001]反 = [0000 0001]补

负整数在计算机却是用补码表示的

负整数：补码=反码+1

[-1] = [1000 0001]原 = [1111 1110]反 = [1111 1111]补 （负数补码=反码+1）

【注：最高位为符号位0表示正，1表示负】

我们来做一个计算，验证这个逻辑：

1 + 1 = 2

[0000 0001]原 + [0000 0001]原 = [0000 0010]原 = 2 没问题

[0000 0001]反 + [0000 0001]反 = [0000 0010]反 = 2 也没问题

[0000 0001]补 + [0000 0001]补 = [0000 0010]补 = 2 也没问题

【结论：正数做加法，原码=反码=补码，结果是很显然的，因为正数的原码=反码=补码，不管采用什么方式计算结果都一样】

我们再来看负数相加的情况：

1 - 1=0----> 1 + (-1) = 0

[0000 0001]原 + [1000 0001]原 = [1000 0010]原 = -2 错误

[0000 0001]反 + [1111 1110]反 = [1111 1111]反 = [1000 0000]原 = -0

【最后1111 1111要还原成原码1000 0000，保留符号位，原来反的再复原】

此时，出现-0这个数，虽然我们能理解0和-0是一个数，但是我们又觉得-0是没有意义的，所以作为人类杰出的发明，当然不允许作为整个人类科技的基石【计算机算科技的基石吧】出现这种没有意义的事情【不完美会让科学家们睡不着】，如果让-0存在，那么就会出现[0000 0000]表示+0，[1000 0000]表示-0，这会浪费一个数[1000 0000]，我们知道，在8位字长中，最高位作为符号位，那么整个8位字长的数能表示的范围就是[1111 1111]~[0111 1111]，即-127~+127，[-127,+127]，这中间还有一个[1000 0000]，所以应该是[-127....-0,0,+127]，计算机的设计者觉得，何不把-0这个编码给到-128，让8位字长能多表示一个数？因此，表示范围变成了[-128,+127]，这样看起来很完美。那，有人说为什么不让-0给+128，让表示范围变成[-127,+128]，但是这个+128怎么编码？又要让最高位的符号位为0，又要表示一个大于127的数【127占满了7个位】，当然是用-0表示-128最好了，因为-128本来符号位就是1啊。

因此，1-1我们不能用反码计算【反码计算结果为-0】。

我们再用补码计算看看，

[0000 0001]补 + [1111 1111]补 = [0000 0000]补 = [0000 0000]原 = 0 【0是一个正数，0的补码，反码，原码都是0000 0000】

补码计算结果正确。

我们刚才做了一个这样得动作：

1-1= 1+（-1）这好像是把减法转成了加法，对没错，计算机就是这样来设计的。那么计算机是如何把减法转成加法的呢？虽然，我们没法搞清楚计算机里面门电路的设计原理，但是可以搞清楚这个理论依据。

计算机是如何把减法转化成加法的？

我们来做一个有意思的实验：

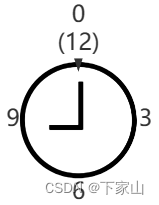
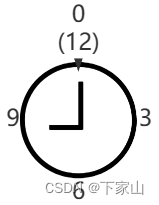例：我们有一个活动定在下午6点，假设当前时间是上午9点，我们要把时钟拨到下午6点的方法，有两种， 一种是倒拨3小时，即9-3 = 6 mod 12 = 6; 还有一种是顺时针拨9小时，即9+9=18 mod 12 = 6； 在以12为模的时钟系统中，加9与减3的效果是一样的。这就很好的把减法转成加法计算了。这就是计算机需要的，因为加法的实现要比减法方便得多。

mod是模运算的意思，2 mod 12 = 2，13 mod 12 = 1， 12 mod 12 = 0，11 mod 12 = 11，

当a mod b = c，a和b都是正整数的时候，你可以把取模运算当成求余运算。

 mod运算的本质是把减法转成加法

（9-3） ≡  (9+9) mod 12 = 6，≡是同余的意思），同余的说明见下面的同余定理，这里先不影响我们理解。

那么补码为什么+1

计算机处理负数的时候，是用补码来计算的，我们上面也证明了，出现负数的时候，必须使用补码才能得出正确答案。而，计算机设计中却规定

  负数的补码 = 反码 + 1

那么这个+1是什么原理？科学家看到-0觉得不完美睡不着，我们看到科学家的补码的设计+1看不懂也睡不着。

我们重新做一遍1-1

反码计算： 1-1=1+(-1)= [0000 0001]原 + [1000 0001]原

= [0000 0001]反 + [1111 1110]反 = [1111 1111]反 = [1000 0000]原 = -0

补码计算: 1-1=1+(-1)=[0000 0001]补 + ([1111 1110]反+0000 0001 ) = [0000 0001]补+[1111 1111]补= 0

+1就对，不加1就错！

[0000 0001] + [1111 1110]反和 [0000 0001] + [1111 1111]补 有什么区别？

这里面是什么原理？

我们回到起点，计算机是想把减法转成加法，当出现负数的时候，用他的同余数来替代。【同余原理下面讲】

再回到钟表：

3-9等价于3+3，我们把-9转成了3，为什么可以这样转变

例：3点要拨到6点， 一种是顺时针拨3个小时，即3+3 = 6 ; 还有一种是逆时针拨9个小时，即3-9 = 6； 注意：你很自然这样操作了！你潜意识里面做了什么？

3-9=6这个等式好像不太对，3-9=-6啊，那么6和-6为什么一样了呢？这就是模的作用？顺时针拨3和逆时针拨9，这3+9=12，12就是这个时钟系统的模。

我们再用数学知识来解释为什么-6和6重合了。

根据mod（模）的公式

X mod y = x - y*⎿ x/y ⏌-------------取模公式

验证：

6 mod 12 = 6 - 12*⎿ 6/12 ⏌ = 6 - 12*⎿ 0.5 ⏌ = 6 - 12*0 = 6 ,符号⎿ ⏌向下取整

-6 mod 12 = -6 - 12 * ⎿ -6/12 ⏌ = -6 - 12 * ⎿ -0.5 ⏌ = -6 - 12*(-1) = -6+12 = 6

看到没有，6和-6 mod 12同余， 6≡-6 mod 12，数学真他妈伟大，所以数学才是基石的基石。【≡，是同余符号】

我们很自然的想到了在钟表里面，3的镜像是-9，也就是3的相反数是-9，或者说-9的相反数是3？

3 mod 12 = 3

-9 mod 12 = -9 - 12 * ⎿ -9/12 ⏌ = -9 - 12 * ⎿ -0.75 ⏌ = -9 - 12*(-1) = -9+12 = 3

那么在钟表里面，-1的相反数是多少？是不是11？

-1 mod 12 = -1 - 12*⎿ -1/12 ⏌ = -1 - 12 * ⎿ -0.09 ⏌ = -1 - 12*(-1) = -1+12 = 11

我们再回到上面1-1的计算中，按照钟表的原理，那么在计算机中-1的镜像是多少？是不是应该是127？

你为什么会想到127？为什么这么自然?

-1的反码是 [1000 0001]原---->[1111 1110]反，这个数如果不看符号位，是多少？是126.

按照钟表的原理，-1的反码不是127吗？

所以，我们要在[1111 1110]反码的基础上再加1【-1的反码是126，补码才是127】，而用补码来表示反码加1.

还是有点牵强！感觉是为了凑这个数。

-1和126有什么关系？【126是取反过来的，为什么要取反？计算机为什么这样设计？】

我们换一种思路：

-1 mod 127 = 126，用数学来解释才是硬道。

-1 mod 127 = -1 - 127*⎿ -1/127 ⏌ = -1 - 127*⎿ -0.008 ⏌ = -1 -127*(-1)=-1+12=126

问题来了，我们上面不是很自然的认为-1的镜像是127吗，为什么我们用数学公式算出来是126？

这就是潜意识里面把模自然当成了128所以，得出-1的相反数是127.

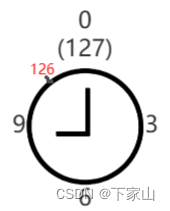
模为127

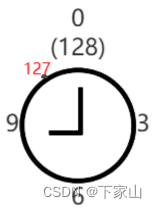
模为128

那为什么不能让-1的相反数直接反过来就等于127呢？

这个做不到，我们看原因

-1反=[1000 0001]原反 = [1111 1110]反=126，而127是[1111 1111](不考虑符号位)

所以，原码取反之后，无法得到127，必须在反的基础上再加1刚好是127。

加1的本质是什么？

加1的本质是让模变成128，这是重点。

那么为什么+1就让模变成了128呢？

我们仔细看上面钟表这个图，当模是127时，表盘上的最大刻度只能是126，如果要让表盘的最大刻度变成127，模必须是128，好好理解这就话。

也许有人说，唉，我用127照样可以对127取模啊，并不是只有小于模的数才可以对该模取模啊。我们要这样想，在模为127的数里面，就没有127这个数，到了127又是一轮了，又归零了，如果你还不好理解，你把模当进制来理解，两个10进制数列竖式计算，里面就不能出现10，满10要进位。

你还可以用127 mod 127 实际上等于0，还是归位到其实位置。

所以，我们在用-1进行计算机运算的时候，必须在反码的基础上加1，只不过我们给这个操作定义一个名字叫补码，本质上是因为-1取反后只能等于126，得不到127才加1的。（加1自然就让mod变成128了）

其实，8位字长的模取值范围是[-128,+127]这个范围的数的模就是128.

【其他字长的原理其实也一样，16位，32位，64位】

至此，补码为什么+1这个问题就解释到这里，不知你是否理解了。

同余定理

两个整数a,b，如果分别除以整数m，得到的余数相等，则称a,b 模 m同余，模常用mod替代。记作：

a ≡ b mod m，≡是同余符号，a和b可以是负数，m一般是正整数(0肯定不可以，不知负数有上面意义，没有去研究)

同余是数论中非常重要的一块，是由德国数学家高斯发明的(1777~1855)，其中同余符号≡就是他发明的。

同余里面的定理：

（1）反身性（Reflexive Property）：若a是整数，则a≡a(mod m)；

这个性质很容易理解，11 mod 7 = 4，11 mod 7 = 4，当然11和11 mod 7 同余；

（2）对称性（Symmetric Property）：若a和b是整数，且a≡b(mod m)，则b≡a(mod m)；

11 mod 7 = 4, 4 mod 7 = 4, 11 ≡ 4 mod 7同余，4 ≡ 11 mod 7也同余

（3）传递性（Transitive Property）：若a、b和c是整数，且a≡b(mod m)和b≡c(mod m)，则a≡c(mod m)。

4 mod 7 = 4, 11 mod 7 = 4， 18 mod 7 = 4,

4 ≡ 11 mod 7，11 ≡ 18 mod 7------> 4 ≡ 18 mod 7

基本模运算

（1）若a≡b(mod m)，c≡d(mod m)，则a±c≡b±d(mod m)；

        4 ≡ 11 mod 7 = 4

        -3 ≡ 18 mod 7 = 4

        1(4+(-3))≡29(11+28) mod 7 = 1, 7(4-(-3))≡-7(11-18) mod 7 = 0

        1(4-3) !≡ -7(11-18) mod 7 前面是a+b后面是a-b这样不同余

（2）若a≡b(mod m)，c≡d(mod m)，则a×c≡b×d(mod m)；

        4 ≡ 11 mod 7 = 4

        2 ≡ 9 mod 7 = 2

        8 ≡ 99 mod 7 = 1

（3）若a≡b(mod m)，且n∈N，     

        2 ≡ 7 mod 5 = 2, 4 ≡ 49 mod 5 = 4 , 8 ≡ 343 mod 5 = 3

（4）若a≡b(mod m)，且k是整数，则k×a≡k×b(mod m)；

        2 ≡ 7 mod 5 = 2, 4 ≡ 14 mod 5 = 4，6 ≡ 21 mod 5 = 1

（5）若a≡b(mod m)，且m＝qn，则a≡b(mod n)

        3 ≡ 15 mod 12 = 3, 12=3x4, 3 ≡ 15 mod 4 = 3, 3≡ 15 mod 3 = 0

        同余定理的目的不是捣鼓这些变换，而是解决问题：比如

Q1）求2的90次方 除以11的余数

红线标注部分，属于取模的一些性质，这些性质可以通过下面的例子看出：

4 mod 11 = 4，有 (4+11) mod 11 = 4，也有 （4 - 11）mod 11 = 4 也就是任何一个数加减n倍的mod的 余数不变，类似钟表6点钟，转一圈还是回到6点，不管是正转还是反转，也不管是转多少圈。

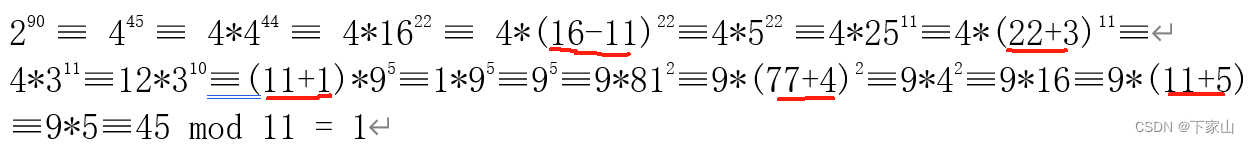
Q2）求1992×59除于7的余数

13 mod 7 = 6 ,有 (1*7 + 6) mod 7 也等于6

9 mod 7 = 2，有(1*7 + 2) mod 7 也等于2

有

13x9 mod 7 = 117 mod 7 = 5

(1*7+6) x (1*7+2) mod 7 = 2*6 mod 7 = 12 mod 7 = 5

所以，1992x59 mod 7 = (1992%7) x (59%7) mod 7 = 4x3 mod 7 = 12 mod 7 = 5

或者，可以这样理解，1992x59 mod 7 = (284*7+4)x(7*8+3) mod 7 = 4x3 mod 7 = 5