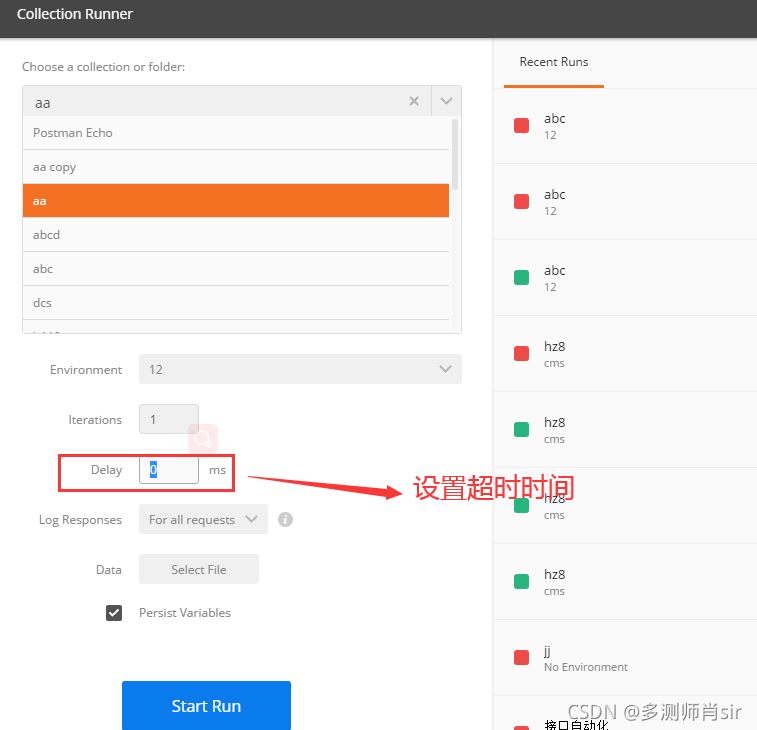
二，量化算术
模型量化过程可以分为两部分：将模型从 FP32 转换为 INT8，以及使用 INT8 进行推理。本节说明这两部分背后的算术原理。如果不了解基础算术原理，在考虑量化细节时通常会感到困惑。
2.1，定点和浮点
定点和浮点都是数值的表示（representation），它们区别在于，将整数（integer）部分和小数（fractional）部分分开的点，点在哪里。定点保留特定位数整数和小数，而浮点保留特定位数的有效数字（significand）和指数（exponent）。
绝大多数现代的计算机系统采纳了浮点数表示方式，这种表达方式利用科学计数法来表达实数。即用一个尾数(Mantissa，尾数有时也称为有效数字，它实际上是有效数字的非正式说法)，一个基数(Base)，一个指数(Exponent)以及一个表示正负的符号来表达实数。具体组成如下：
- 第一部分为
sign符号位 s，占 1 bit，用来表示正负号； - 第二部分为
exponent指数偏移值 k，占 8 bits，用来表示其是 2 的多少次幂； - 第三部分是
fraction分数值（有效数字） M，占 23 bits，用来表示该浮点数的数值大小。
基于上述表示，浮点数的值可以用以下公式计算：
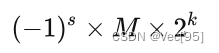
值得注意是，上述公式隐藏了一些细节，如指数偏移值 k 使用的时候需要加上一个固定的偏移值。
比如 123.45 用十进制科学计数法可以表示为 1.2345×102 ，其中 1.2345 为尾数，10 为基数，2 为指数。
单精度浮点类型 float 占用 32bit，所以也称作 FP32；双精度浮点类型 double 占用 64bit。
量化浮点
32-bit 浮点数和 8-bit 定点数的表示范围如下表所示：
| 数据类型 | 最小值 | 最大值 |
|---|---|---|
| FP32 | $-1.2\times 10^{-38}$ | $3.4\times 10^{38}$ |
| int8 | -128 | 128 |
| uint8 | 0 | 255 |
值 2127 大约等于 1038。
神经网络的推理由浮点运算构成。FP32 和 INT8 的值域是 [(2−223)×2127,(223−2)×2127] 和 [−128,127] ，而取值数量大约分别为 232 和 28 。FP32 取值范围非常广，因此，将网络从 FP32 转换为 INT8 并不像数据类型转换截断那样简单。但是，一般神经网络权重的值分布范围很窄，非常接近零。
根据偏移量 Z是否为 0，可以将浮点数的线性量化分为两类-对称量化和非对称量化。
当浮点值域落在 (−1,1) 之间，权重浮点数据的量化运算可使用下式的方法将 FP32 映射到 INT8，这是对称量化。其中 
表示 FP32 权重， 表示量化的 INT8 权重， 
是缩放因子（映射因子、量化尺度（范围）/ float32 的缩放因子）。
对称量化的浮点值和 8 位定点值的映射关系如下图，从图中可以看出，对称量化就是将一个 tensor 中的
内的 FP32 值分别映射到 8 bit 数据的 [-128, 127] 的范围内，中间值按照线性关系进行映射，称这种映射关系是对称量化。可以看出，对称量化的浮点值和量化值范围都是相对于零对称的。
因为对称量化的缩放方法可能会将 FP32 零映射到 INT8 零，但我们不希望这种情况出现，于是出现了数字信号处理中的均一量化，即非对称量化。数学表达式如下所示，其中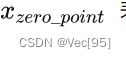 
表示量化零点（量化偏移）。
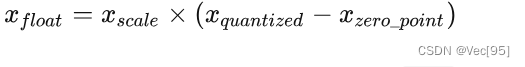
大多数情况下量化是选用无符号整数，即 INT8 的值域就为 [0,255] ，这种情况，显然要用非对称量化。非对称量化的浮点值和 8 位定点值的映射关系如下图：
