198.打家劫舍 

这个题一开始由于给出来的例子陷入了思维误区，以为结果就是每隔一个取一个，其实有可能中间隔很多个。比如一下这个例子

下面这种写法不对。

class Solution {
public:
    int rob(vector<int>& nums) {
        int odd_sum = 0;
        int even_sum = 0;
        for( int i = 0; i < nums.size(); i = i + 2){
            odd_sum += nums[i];
        }

         for( int j = 1; j < nums.size(); j = j + 2){
            even_sum += nums[j];
        }
         return max(odd_sum, even_sum);
    }
};

下面这种动态规划才能做出来；

class Solution {
public:
    int rob(vector<int>& nums) {
        if (nums.size() == 0) return 0;
        if (nums.size() == 1) return nums[0];
        vector<int> dp(nums.size() + 1, 0); //dp[i]：考虑下标i（包括i）以内的房屋，最多可以偷窃的金额为dp[i]。
        dp[0] = nums[0];
        dp[1] = max (nums[0], nums[1]);
        for (int i = 2; i < nums.size(); i++) {
            dp[i] = max(dp[i - 1], dp[i - 2] + nums[i]);
        }
        return dp[nums.size() - 1];
    }
};

213.打家劫舍II

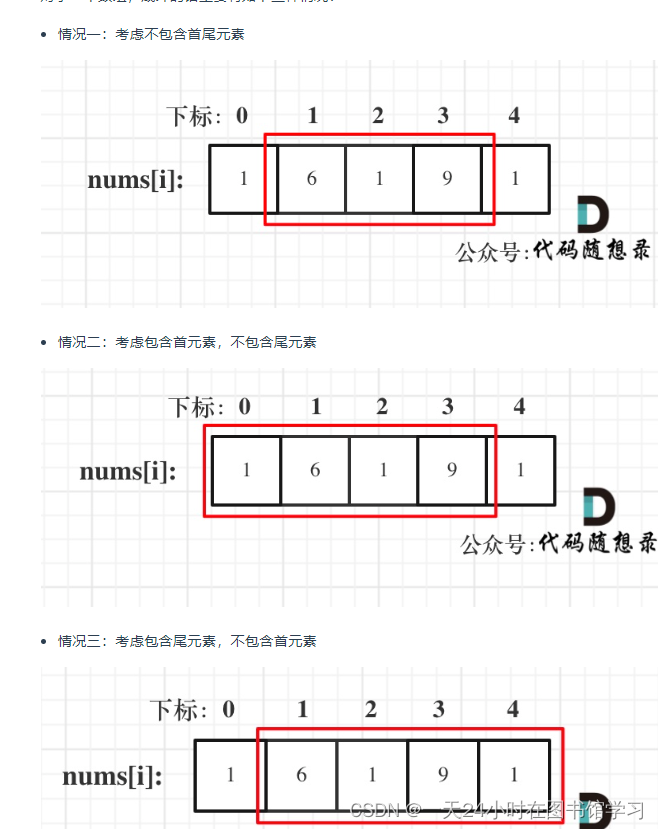
情况二就是假设不存在最后一个元素来求最大可以偷的， 情况上就是假设不存在第一个元素来求最大可以偷的，具体情况二选不选择首元素这个要看递推公式来决定；

class Solution {
public:
    int rob(vector<int>& nums) {
        if (nums.size() == 0) return 0;
        if (nums.size() == 1) return nums[0];
        int result_1 = robRange(nums, 0, nums.size() - 2);
        int result_2 = robRange(nums, 1, nums.size() - 1);
        return max(result_1, result_2);
    }

    int robRange(vector<int>& nums, int start, int end) {
        if (end == start) return nums[start];  //这行不写会报错越界之类的
        vector<int> dp(nums.size(), 0);
        dp[start] = nums[start];
        dp[start + 1] = max(nums[start], nums[start + 1]);
        for (int i = start + 2; i <= end; i++) {
            dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
        }
        return dp[end];
    }
};

337.打家劫舍 III

树形dp，后序遍历。挺难的做不出； dp的含义是dp[0]是不屈这个current的最大值，dp[1]是取这哦current的最大值

class Solution {
public:
    int rob(TreeNode* root) {
        vector<int> result = robTree(root);
        return max(result[0], result[1]);
    }
    // 长度为2的数组，0：不偷，1：偷
    vector<int> robTree(TreeNode* cur) {
        if (cur == NULL) return vector<int>{0, 0};
        vector<int> left = robTree(cur->left);
        vector<int> right = robTree(cur->right);
        // 偷cur，那么就不能偷左右节点。
        int val1 = cur->val + left[0] + right[0];
        // 不偷cur，那么可以偷也可以不偷左右节点，则取较大的情况
        int val2 = max(left[0], left[1]) + max(right[0], right[1]);
        return {val2, val1};
    }
};