1.状态分析

我们可以把无符号数分为：整数，带小数，带指数部分三种形式。以此构建一个DFA。首先需识别输入是整数还是小数点，若是整数部分输入然后还要再循环识别一次是否有小数点，最后识别是否有指数部分，指数部分可以带有符号。

2.画出状态图

下图种d代表整数，不在状态图中的情况则表示这不是无符号数

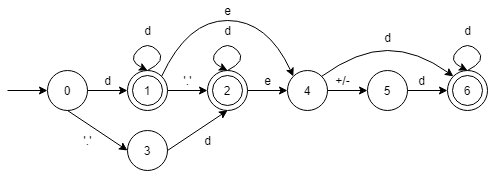
3.构造状态矩阵

状态图种不存在的情况则标为-1

	.	E/e	+/-	d	other
0	3	-1	-1	-1	-1
1	2	4	-1	1	-1
2	-1	4	-1	2	-1
3	-1	-1	-1	2	-1
4	-1	-1	5	6	-1
5	-1	-1	-1	6	-1
6	-1	-1	-1	6	-1

4.程序实现

#include <iostream>
#include <string>
using namespace std;

// 状态转换表0: . 1: e 2: + or - 3: 0-9 4: other
int state[7][5] = {
    {3, -1, -1, 1, -1},
    {2, 4, -1, 1, -1},
    {-1, 4, -1, 2, -1},
    {-1, -1, -1, 2, -1},
    {-1, -1, 5, 6, -1},
    {-1, -1, -1, 6, -1},
    {-1, -1, -1, 6, -1}
};
int allend[3] = {1, 2, 6}; //可以结束的状态

int judge(char change) {
    if (change == '.') return 0;
    else if (change == 'E' || change == 'e') return 1;
    else if (change == '+' || change == '-') return 2;
    else if (change >= '0' && change <= '9') return 3;
    else return 4;
} //跳转函数

int isend(int now) {
    for (int i = 0; i < 3; i++) {
        if (now == allend[i]) return 1;
    }
    return 0;
} // 判断是否为结束状态

int main() {
    string s;
    while (cin >> s) {
        int now = 0;
        for (int i = 0; i < s.length(); i++) {
            cout << now << "->";
            int index = judge(s[i]);
            now = state[now][index];
            cout << now << endl;
            if (now == -1) break; // 发现不是无符号数
        }
        if (isend(now) == 1) cout << "yes\n";
        else cout << "no\n";
    }
    return 0;
}