深入浅出排序算法之希尔排序

news2024/9/25 9:37:54

1. 原理

2. 代码实现

3. 性能分析

1. 原理

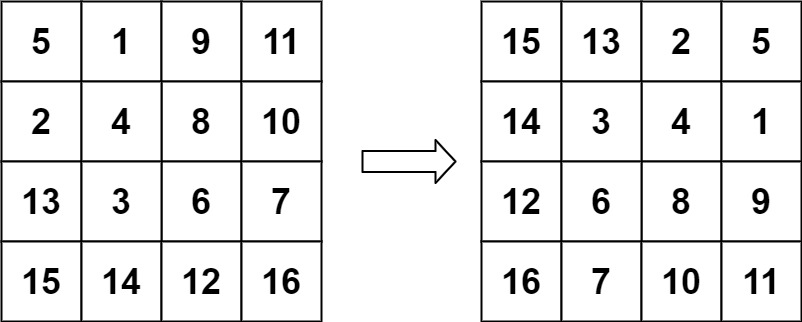
希尔排序法又称缩小增量法。希尔排序法的基本思想是：先选定一个整数，把待排序文件中所有记录分成个组，所有距离为的记录分在同一组内，并对每一组内的记录进行排序。然后，取，重复上述分组和排序的工作。当到达=1时，所有记录在统一组内排好序。

（1）希尔排序是对直接插入排序的优化。
（2）当gap > 1时都是预排序，目的是让数组更接近于有序。当gap == 1时，数组已经接近有序的了，这样就会很快。这样整体而言，可以达到优化的效果。我们实现后可以进行性能测试的对比。

2. 代码实现

    //希尔排序
    public static void shellSort(int[] array){
        int gap = array.length;
        while(gap > 1){
            shell(array,gap);
            gap /= 2;//增量是多少都可以，随便小伙伴们写
        }
        shell(array,1);
    }
    //有增量的直接插入排序
    //不是一组希尔排序全部排完，是间隔性的，可能是第一组先插一个，第二组再插一个，第一组再插……
    private static void shell(int[] array,int gap){
        for(int i = gap;i < array.length;i++){
            int tmp = array[i];
            int j = i - gap;
            for(;j >= 0;j -= gap){
                if(array[j] > array[j+gap]){
                    array[j + gap] = array[j];
                }
                else{
                    break;
                }
            }
            array[j + gap] = tmp;
        }
    }


    public static void main(String[] args) {
        int[] arr = {3,1,2,4,5};
        Sort.shellSort(arr);
        for (int x : arr) {
            System.out.print(x + " ");
        }
    }

3. 性能分析

时间复杂度			空间复杂度
最好	平均	最坏	空间复杂度
O(N)	O(N^1.3)	O(N^2)	O(1)
数据有序		难以构造出来

    public static void main(String[] args) {

        int[] arr2 = new int[10000];
        Test.createArray2(arr2);
        long s2 = System.currentTimeMillis();
        Sort.insertSort(arr2);
        long e2 = System.currentTimeMillis();
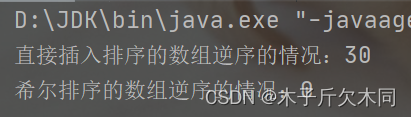
        System.out.println("直接插入排序的数组逆序的情况："+(e2 - s2));

        int[] arr1 = new int[10000];
        Test.createArray2(arr1);
        long s1 = System.currentTimeMillis();
        Sort.shellSort(arr2);
        long e1 = System.currentTimeMillis();
        System.out.println("希尔排序的数组逆序的情况："+(e1 - s1));
    }