问题描述

小蓝是一个热爱收集玩具的小伙子，他拥有  n 个不同的玩具。

这天，他把  n 个玩具按照高度顺序从矮到高摆放在了窗台上，然后，他希望将这些玩具分成  k 个段，使得所有分段的极差之和尽可能小。

具体来说，你需要将一个长度为  n 的序列分为  k 段，我们定义  Gi 为第  i 个分段的极差，你要最小化 。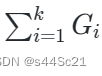

你能帮助小蓝找到最小值是多少吗？

极差：是指每个分段中最高和最矮玩具高度之差，例如有一段为： {3,6,10,12}，那么极差为  12−3=9。

分段：即每一段在原始序列中是一段连续区间，例如将  {1,2,3,4,5} 分为两段， {1,2,3}∣{4,5} 是合法的，但是  {1,2,4}∣{3,5} 不是合法的。

输入格式

第一行输入两个整数  n,k，代表玩具数量和需要分段的数量。

第二行输入  n 个整数  {h1,h2,...,hn}，代表每个玩具的高度。

输出格式

输出一个整数，表示最小的极差和。

样例输入

5 2 
2 5 7 10 13

样例输出

8

说明

存在多种分段方式，其结果都是最小值：

1. {2}∣{5,7,10,13}，极差和为 0+8=8。
2. {2,5,7}∣{10,13}，极差和为 5+3=8。
3. {2,5,7,10}∣{13}，极差和为 8+0=8。

评测数据范围

1≤k≤n≤10^5。

1≤h1≤h2≤h3≤...≤hn≤10^9。

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int n=scan.nextInt();
        int k=scan.nextInt();
        int sum=0;
        int a[]=new int[n];
        int b[]=new int[n-1];
        for(int i=0;i<n;i++){
            a[i]=scan.nextInt();
        }
        for(int i=0;i<n-1;i++){
            b[i]=a[i+1]-a[i];
        }
        Arrays.sort(b);
        for(int i=0;i<n-k;i++){
            sum+=b[i];
        }
        System.out.println(sum);
    }
}