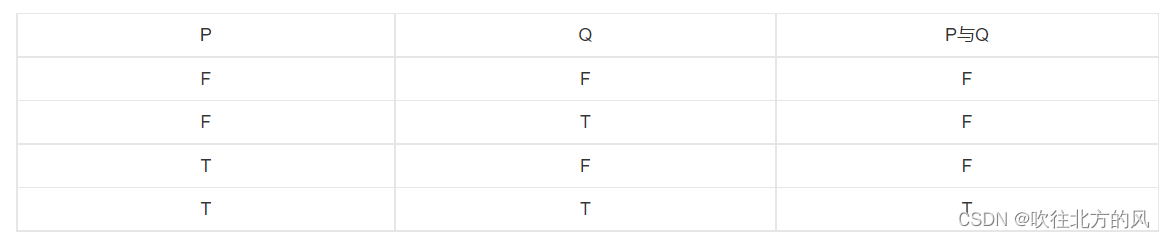
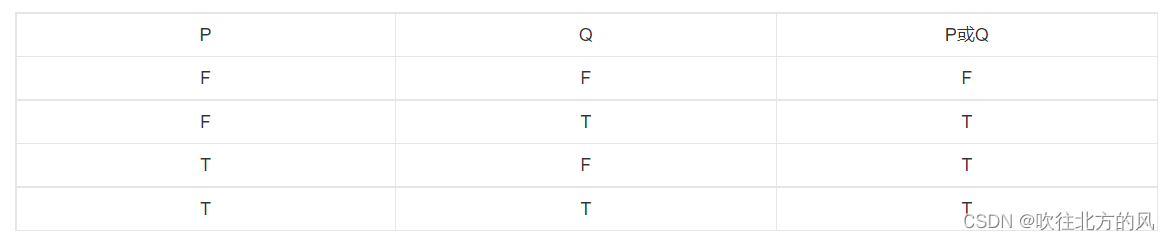
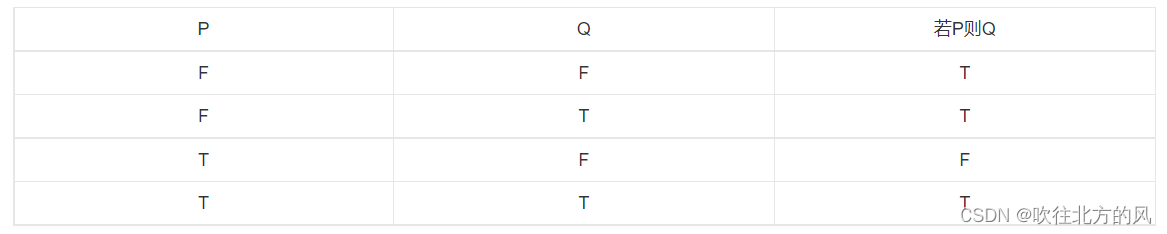
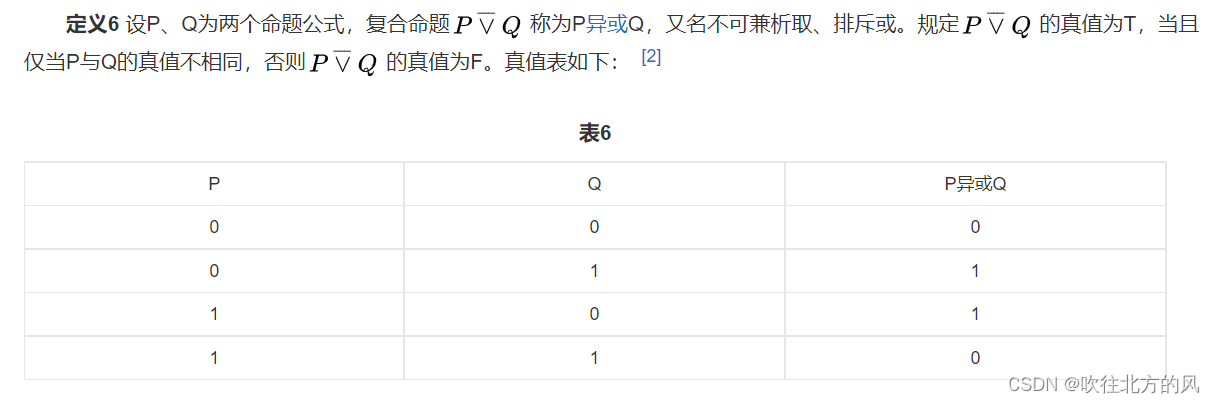
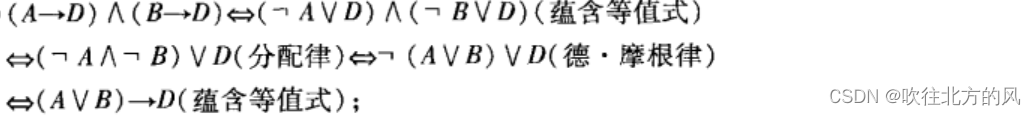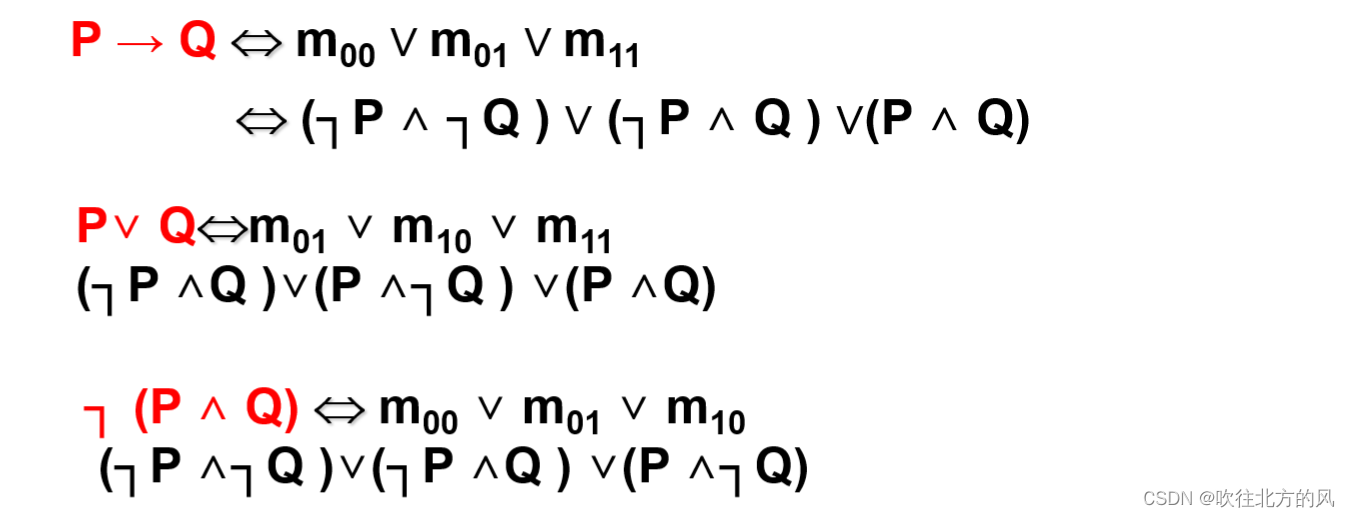复习16题： 

【1】下列哪个语句是真命题（）

A、今天天气真好！

B、我正在说谎。

C、如果7 + 2 = 10 ，那么4 + 6 = 5。

D、如果7 + 2 = 9 ， 则 4 + 6 = 5。

---

对于A，只有具有确定真值的陈述句才是命题，因此感叹句、疑问句、祈使句等不能作为命题。

对于B，“我正在说谎” 是不能确定真值的，是一个悖论！

对于C，p -> q ，前假后真是一个真命题。

对于D，p -> q，前真后假是一个假命题。

答案是C。

【2】下列语句中是真命题的是（）
A、1 + 101 = 110。

B、严禁吸烟！
C、如果1+2=3，那么雪是黑的。

D、如果1+2=5，那么雪是黑的 。

---

根据上面那道题，练一下这道题！

对于A在二进制中为真，在十进制中为假，所以无法判断其真值。

答案是D。 

【3】 令P：他聪明 ， Q：他用功 ， 则命题“虽然他聪明，但是他不用功”可符号化为（）

---

否定："" 理解为“不……”，表示否定。

合取：""理解为“……与……”，但不能局限于此，比如“虽然……，但是……”这种类似“与”相并列意思的命题。

析取：""理解为“……或……”。

条件：“”理解为“如果……那么……” 或者“若……则……”。

双条件：“”可理解为“……当且仅当……”。

【4】将下列命题符号化：

1、如果a 和 b是偶数，则a + b 是偶数。

2、四边形 ABCD是平行四边形，当且仅当它的对边平行。

3、停机的原因在于语法错误或程序错误。

4、小李一边看书，一边听音乐。

---

根据上面那道题，练一下这道题。

 【5】若要使公式的真正为真，则P和Q的赋值分别是（）。

---

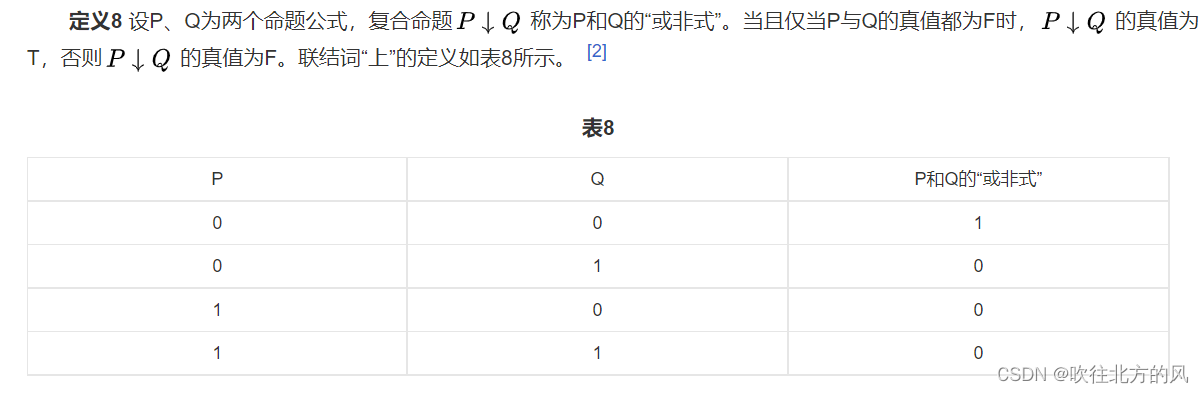
⚠️必记：欲会此题，必先知道联结词的真值组合。

---

有些学校可能也会考察其他的联结词：

异或联结词：

与非联结词：

或非联结词：

条件否定：

P	Q	P和Q的条件否定
T	T	F
T	F	T
F	T	F
F	F	F

 【6】写出   的真值表，并求它们的成真赋值和成假赋值?

【7】证明下列等价式：

(a）

或者：

---

(b)

蕴析律（蕴含等价式）：

---

(c)

---

当然上面这些题都可以通过画出真值表来对比是否等价（笨方法）

比如：

通过真值表证明：

P	Q
T	T	T	T	F	T
T	F	F	F	F	F
F	T	F	F	F	F
F	F	T	F	T	T

它们的真值是相同的，所以其等价！

---

⚠️必记

【8】下列等价式正确的是（）

---

答案：D

 【9】证明下列各式是重言式？

1、

法一，直接证明：（用上面那个等价律表）

法二，画真值表看是否为真（笨方法）

---

2、

也可以用蕴含重言式证明：

定理：当且仅当 P -> Q是一个重言式时，我们称“P蕴含Q”，即

---

【10】 

【11】 不构造真值表法证明此蕴含式：

1、

解法一（前真看后真）：

解法二（后假看前假）：

解法三（定理：当且仅当 P -> Q是一个重言式时，我们称“P蕴含Q”，即）：

---

有些时候也会考察 P -> Q的逆换式、反换式、逆反式。

【12】

一个一个带入进去，比如A。

我们用【后假看前假】

若S V R为假，则S为假，R为假。

所以我们讨论

（1）P和Q都为真

（2）P真Q假

（3）P假Q真

（4）P和Q都是假

讨论完后，发现前式都是假的，所以选择A。

---

这题用推理来证也很简单（见后文）

【13】 

答案：D

复习见P32

【14】 

答案：C

复习见P29

【15】 

求主析取范式：

法一：真值表法：

在真值表中,一个公式的真值为T的指派所对应的小项的析取,即为此公式的主析取范式。

例如：      

所以：

法二：利用基本等价公式推出

---

同理对于主合取范式方法类似：

在真值表中,一个公式的真值为F的指派所对应的大项的合取,即为此公式的主合取范式。

更多请见P38

---

例题：

答案：C

【16】 

答案：C（注意是不能推出）

有三种方法：

【1】真值表法

【2】直接证法

【3】间接证法

具体步骤，请见P40

 

---

基础选择题：

答案：

1：D 

2：B

3：A

4：A

5：D

6：C

7：C

8：A

9：A

10：A 

11：B

---

基础填空题：

答案：

1：（1，0，0） ，（1，0，1），（1，1，1）

2：1

3： ，

4：T

5：

6： ，

、、

7、

8、永假（矛盾）、永真（重言）

结尾：

相信我，刷完这些题，你第一章必定学的巴巴实实的！！