一、单链表，循环链表和双向链表的时间效率比较

	查找表头结点（首元结点）	查找表尾结点	查找结点*p的前驱结点
带头结点的单链表L	L->next时间复杂度O（1）	从L->next依次向后遍历时间复杂度为O（n）	通过*p无法找到其前驱
带头结点仅设头指针为L的循环单链表	L->next时间复杂度为0（1）	从L->next依次向后遍历时间复杂度为O（n）	通过p->next可以找到其前驱时间复杂度为O(n)
带头结点仅设尾指针R的循环链表	R->next时间复杂度为O（1）	R时间复杂度O（1）	通过p->next可以找到其前驱的时间复杂度O（n）
带头结点的双向循环链表L	L->next时间复杂度为O(1)	L->prior时间复杂度为O（1）	p->prior时间复杂度为O（1）

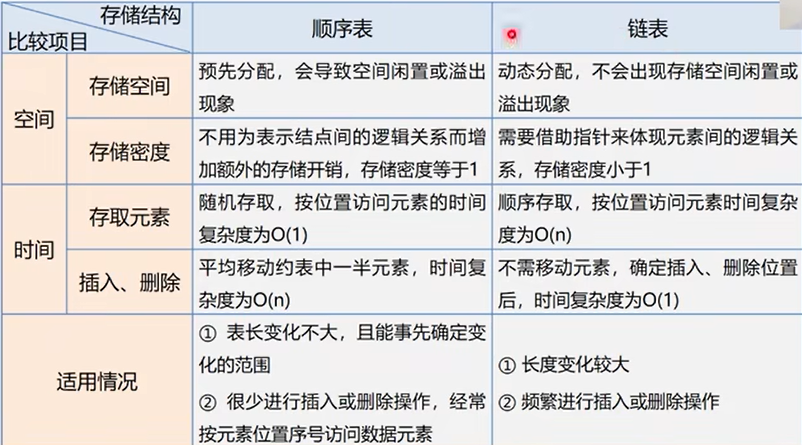
二、顺序表和链表的比较

• 链式存储结构的优点：
  结点空间可以动态申请和释放；
  数据元素的逻辑次序靠结点的指针来指示，插入和删除不需要移动数据元素。
• 链式存储结构的缺点：
  存储密度小，每个结点的指针域额外需要占用存储空间。（存储密度是指结点数据本身所占的存储量和整个结点结构中所占的存储量之比），即：（结点本身占用的空间）/(节点占用的空间总量））
  
  一般的，存储密度越大，存储空间的使用率就越高。显然，顺序表的存储密度为1（100%），而链表的存储密度小于1.
• 链式存储结构非随机存储。
  

三、线性表的应用

1.线性表的合并

假设利用两个线性表La和Lb分别表示两个集合A和B，现要求一个新的集合A = A∪B。

【算法步骤】
依次取出Lb中的每一个元素，执行以下操作：
1.在La中查找该元素。
2.如果找不到，则将其插到La的最后。

1.1有序表的合并------用顺序表实现

已知线性表La和Lb中的数据元素按值递增有序排列，现要求将La和Lb归并为一个新的线性表Lc，且Lc也按递增排列。

//线性表的合并
void Union(Sqlist La, Sqlist Lb) {
	int La_len = La.length;
	int Lb_len = Lb.length;
	for (int i = 1; i <= La.length; i++) {
		Elemtype e;
		GetElem(Lb, i, e);//查找Lb中的第i个元素，若果存在就赋值给e
		if (!LocateElem(La, e, i)) {//La中不存在与e相同的元素
			//将e插在La的最后
			int m = 0;
			ListInsert(La, ++m, e);
		}
	}
}

1.2有序表的合并--------用链表实现

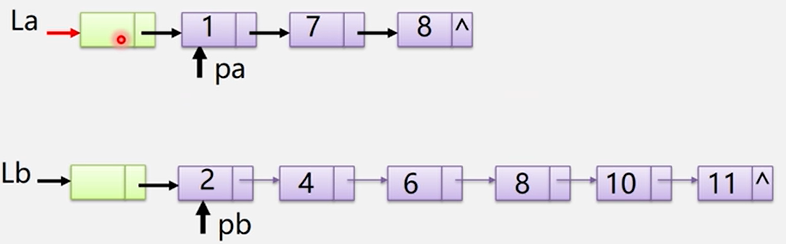
①将La的头结点作为Lc的头结点（Lc表示最后合并好的链表）。
②指定三个三个结点

③比较La和Lb的结点的指针指向的数据域的大小：pa->data < pb->data；那个小的pa连接到Lc上：pc->next = pa就将小的那个链表放进Lc中。
④将pa复制给pc：pc=pa；pa指向下一个结点。
⑤再比较pa和pb的大小，这里的pb比较小，所以在pc后面接上pb：pc->next= pb；

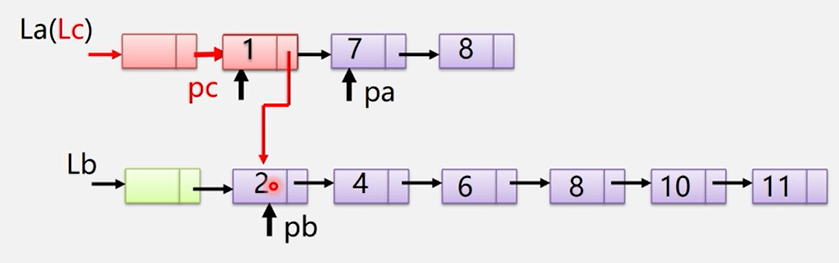
⑥再将pb赋值给pc;pb往后面移pc=pb->next；
⑦继续比较pa->data和pb->data的值
⑧直到将某一个链表的结点都加入了，就完成链表的合并。

⑨如果哪个链表非空，就指向哪个链表：pc->next = pa ? pa:pb;

void MergeList(LinkList& La, LinkList& Lb, LinkList& Lc) {
	LinkList pa = La->next;
	LinkList pb = Lb->next;
	LinkList pc = Lc = La;
	while (pa && pb) {
		if (pa->data <= pb->data) {
			pc->next = pa;
			pc = pa;
			pa = pa->next;
		}
		else {
			pc->next = pb;
			pc = pb;
			pb = pb->next;
		}
	}
	pc->next = pa ? pa : pb;//如果pa非空那么pc->next = pa，否则pb
	delete Lb;//释放Lb的头结点
}