Kalman-Filter-Example

项目地址 https://github.com/zhengjie9510/kalman-filter-example

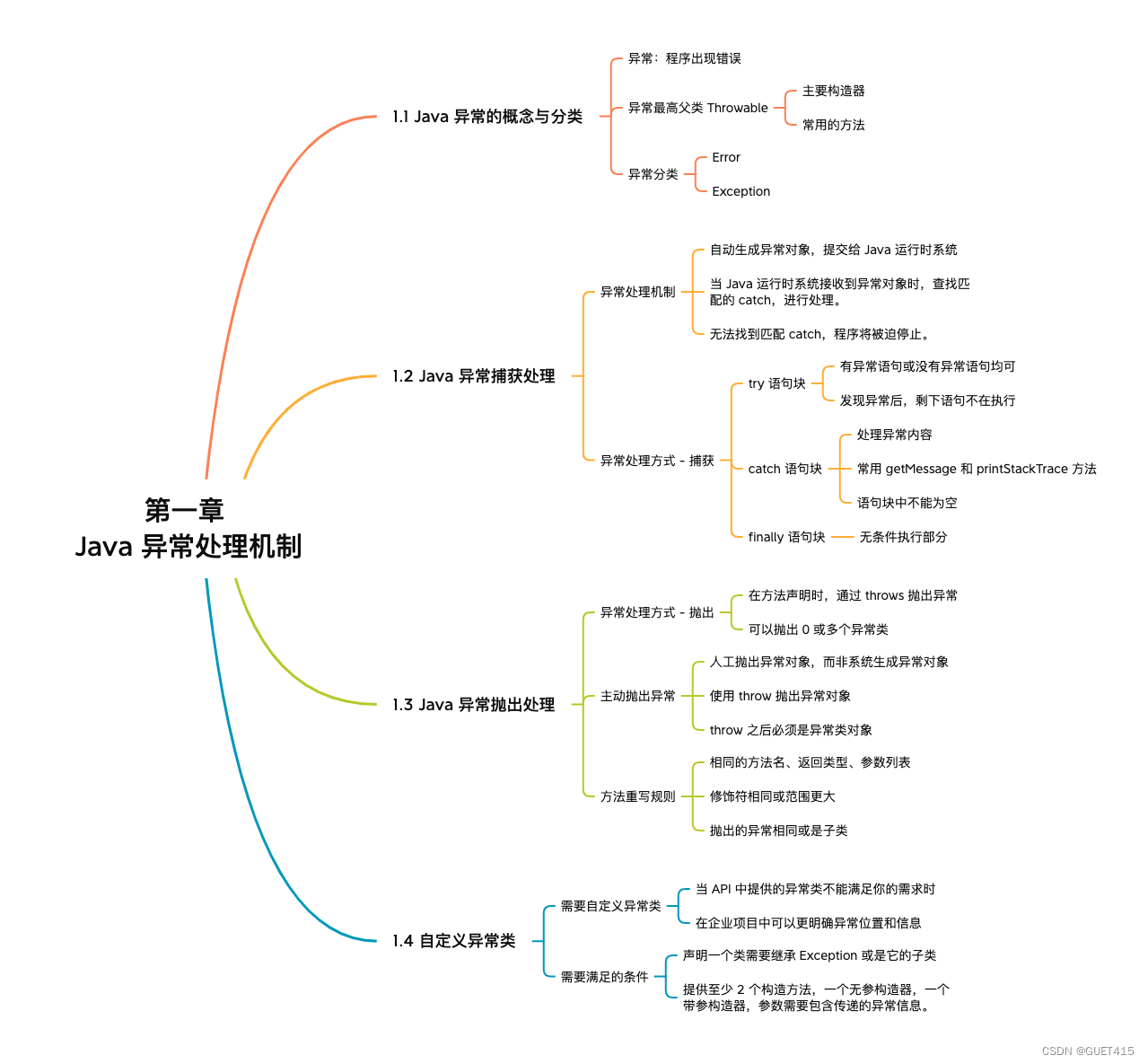
理论公式

详细理论可参考DR_CAN关于卡尔曼滤波器的视频讲解。https://www.bilibili.com/video/BV1dV411B7ME
卡尔曼滤波公式分为预测和更新两部分。

预测公式为：

x_hat_minus[k]= A * x_hat[k-1] + B * u[k-1]

P_minus[k] = A * P[k-1] * A.T + Q

更新公式为：

K[k] = P_minus[k] * H.T * (H * P_minus[k] * H.T + R).I

x_hat[k] = x_hat_minus[k] + K[k] * (z[k] - H * x_hat_minus[k])

P[k] = (np.eye(1) - K[k] * H) * P_minus[k]

其中:

x_hat_minus--先验估计状态  
P_minus--先验估计协方差矩阵  
x_hat--后验估计状态  
P--后验估计协方差矩阵  
A--状态转移矩阵  
B--控制矩阵  
u--控制量  
Q--过程噪声协方差矩阵  
K--卡尔曼增益  
H--观测矩阵  
R--观测噪声协方差矩阵  
z--观测量。

应用

背景

假定有一个匀速运动的人，状态变量x1和x2，Xx1表示人的位置，x2表示人的速度，观测变量z1和z2，z1表示人的位置，z2表示人的速度。
状态转移方程如下：

速度：x2[k] = x2[k-1] + w2[k-1]  
位置：x1[k] = x1[k-1] + x2[k-1] * dt + w1[k-1]

测量方程为：

速度：z2[k] = x2[k] + v2[k]  
位置：z1[k] = x1[k] + v1[k]

读取数据

df = pd.read_csv('data.csv', index_col=0)
x = df[['X1', 'X2']].values
z = df[['Z1', 'Z2']].values

设置参数并调用卡尔曼滤波函数

u = np.zeros(z.shape)  # 控制量，当前场景为0
x_hat_first = np.array([[0, 1]])  # 初始估计
P_first = np.array([[1, 0], [0, 1]])  # 初始估计协方差

A = np.array([[1, 1], [0, 1]])  # 状态转移矩阵
B = np.array([[0, 0], [0, 0]])  # 控制矩阵
H = np.array([[1, 0], [0, 1]])  # 观测矩阵
Q = np.array([[0.1, 0], [0, 0.1]])   # 系统噪声协方差矩阵
R = np.array([[1, 0], [0, 1]])  # 测量噪声协方差矩阵

x_hat = kalman_filter(x, z, u, A, B, H, Q, R, x_hat_first, P_first)

结果展示

plt.figure(figsize=(16, 9))
plt.plot(x[:, 0], 'g--', label='position--noisy system estimate')
plt.plot(z[:, 0], 'k--', label='position--noisy measurements')
plt.plot(x_hat[:, 0], 'b--', label='position--a posteri estimate')
plt.legend()
plt.xlabel('Step')
plt.ylabel('Position')
plt.title('Position')
plt.show()

plt.figure(figsize=(16, 9))
plt.plot(x[:, 1], 'g-', label='speed--noisy system estimate')
plt.plot(z[:, 1], 'k-', label='speed--noisy measurements')
plt.plot(x_hat[:, 1], 'b-', label='speed--a posteri estimate')
plt.legend()
plt.xlabel('Step')
plt.ylabel('Speed')
plt.title('Speed')
plt.show()