•  139.单词拆分 

•  关于多重背包，你该了解这些！ 

•  背包问题总结篇！

第一题：单词拆分

给定一个非空字符串 s 和一个包含非空单词的列表 wordDict，判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。

说明：

拆分时可以重复使用字典中的单词。

你可以假设字典中没有重复的单词。

示例 1：

• 输入: s = "leetcode", wordDict = ["leet", "code"]
• 输出: true
• 解释: 返回 true 因为 "leetcode" 可以被拆分成 "leet code"

感觉用背包做这道题不是很好理解。

单词作为物品，字符串S就是背包，单词能否组成字符串S，就是问物品能不能把背包装满，意思就是说字符串的单词必须全部由单词表里的部分单词组成？

动态规划五部曲：

（1）确定dp数组以及下标含义

dp[i]: 字符串长度为i的话，dp[i]为true，表示可以拆分成一个或多个在字典中出现的单词。

（2）确定递推公式

站在前面往后看，如果dp[j]=true的话，且[j,i]这个区间的子串出现在字典中，那么dp[i]一定也是true;

就是说，如果前面已经是true了，后面的子串也在字典中，自然dp[i]就是true，如果前面是true，但是子串没在字典中，那么dp[i]是false

（3）dp数组如何初始化。

根据递推公式dp[i]依赖dp[j]，所以dp[0]就是根基，比如(0,1)子串在字典中，那么dp[1]是否是true就取决于dp[0]了，所以dp[0]肯定为true;

（4）确定遍历顺序

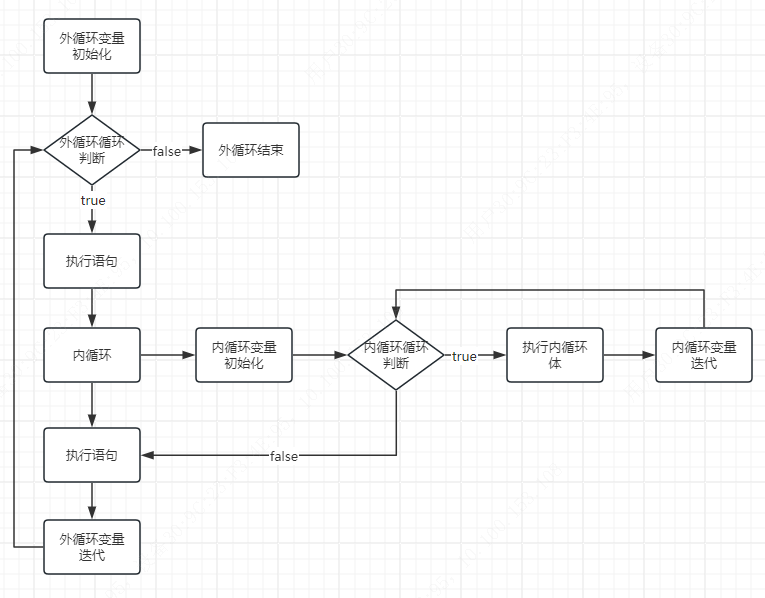
本题，物品（单词）可以无限次使用，目的是将背包装满，同时单词的拿取有顺序，只有这样才能组成正确的字符串。所以是排列问题

排列问题：外层先遍历背包，内层后遍历物品。

（5）举例推导dp[i]

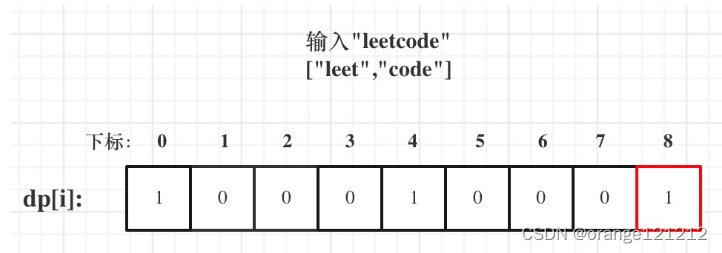
第二题：多重背包问题

有N种物品和一个容量为V的背包，第i种物品最多有Mi件可用，每件耗费的空间是Ci，价值是Wi。

求解将哪些物品装入背包可使这些物品的耗费的空间总和不超过背包容量，且价值总和最大。

和之前的不同：物品数量不一样。但将所有物品张开其实和01背包一样。

背包问题总结：

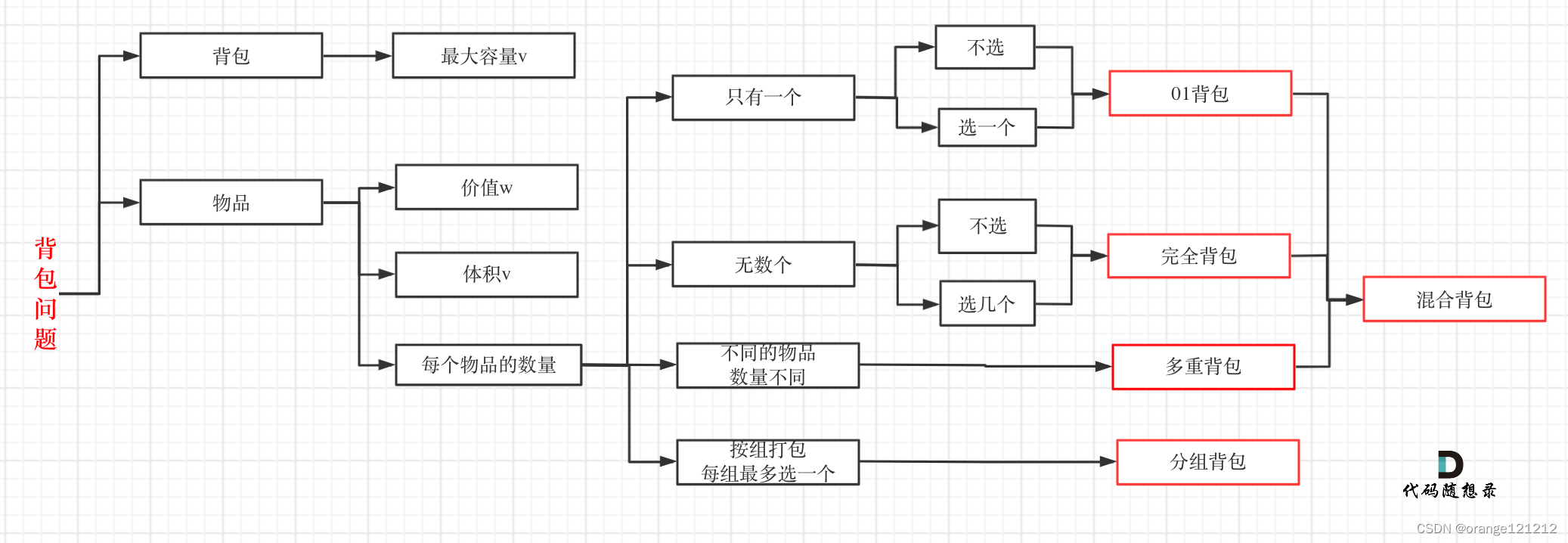
不论题目如何描述，涉及容量的是背包，涉及价值体积数量的是物品。

动态规划五部曲：

1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式
3. dp数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组

重点在递推公式，初始化根据递推公式决定dp[0]的值

1. 问能否装满背包（或者最多装多少）：dp[j]=max(dp[j],dp[j-nums[i]]+nums[i]);

分割等和子集：用一个容量为sum/2的背包装子集

最后一块石头的重量：同理，用一个容量为sum/2的背包装子集，并求最后剩下的

2. 问装满背包有几种方法： dp[j]+=dp[j-nums[i]];

目标和：站在j位置上，等于原来的j-nums[i]的基础上加上nums[i].

零钱兑换2:

组合总和4

爬楼梯进阶版

3. 问背包装满最大价值：dp[j]=max(dp[j],dp[j-weight[i]]+value[i])

一和零：等等，有些不理解

4.问装满背包所有物品的最小个数：dp[j]=min(dp[j-coins[i]]+1,dp[j])

零钱兑换：用5,10,20装满背包

完全平方数：将满足条件的数求平方和满足target，等于求装满背包，只是多加了一步求平方

遍历顺序：

01背包：注意一维dp数组和二维dp数组

完全背包：一维dp数组实现，但是for循环的先后不一样

如果是求组合，外层先物品，内层再背包

如果是求排列，外层先背包，内层再物品

求组合数：零钱兑换2

求排列数：组合总和4、爬楼梯进阶版

求最小数：零钱兑换、完全平方数