个人主页:仍有未知等待探索_C语言疑难,数据结构,小项目-CSDN博客
专题分栏:数据结构_仍有未知等待探索的博客-CSDN博客
目录
一、前言
二、队列的基本操作(循环队)
1、循环队的数据类型
2、循环队的名词解释
3、循环队的创建及其初始化
第一种写法
第二种写法
4、 判断队满
5、判断队空
6、入队
7、出队
8、求长度
三、优势
四、总代码
一、前言
在前面学习了栈的基本知识,知道栈是一种特殊的线性表,其特点是先进后出。
而接下来要学的队列也是一种操作受限的线性表,其特点是先进先出。从队头出队,从队尾入队。
二、队列的基本操作(循环队)
1、循环队的数据类型
在下面的数据类型实现中,存数据的data数组的类型有两种写法。
第一种写法:这样写的话,数组是固定的MAX大小。
//第一种写法 elemtype data[MAX];
第二种写法:这样写的话,可以通过动态内存开辟来给data开辟足够大的空间。
//第二种写法 elemtype* data;
front和rear的作用是记录对头位置和队尾位置。
由下图可以清晰的看出:
front:指向第一个元素。
rear:指向最后一个元素的下一个元素。
#define MAX 100
typedef int elemtype;
typedef struct Queue
{
//第一种写法
//elemtype data[MAX];//elemtype是为了改data的数据类型的时候方便
//第二种写法
elemtype* data;
int front;//队首指针
int rear;//队尾指针
}Queue;2、循环队的名词解释
可能大家一开始都会有疑问,为什么叫做循环队呢?栈用数组进行存储叫做顺序栈,为什么队列用数组存储叫做循环队呢?
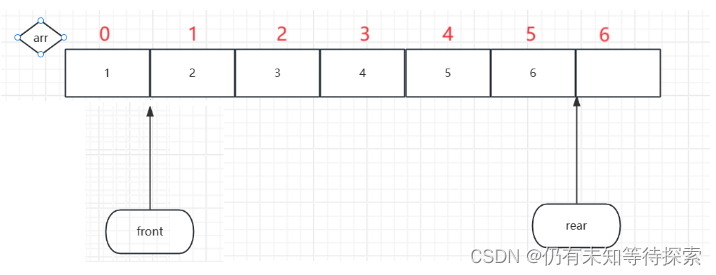
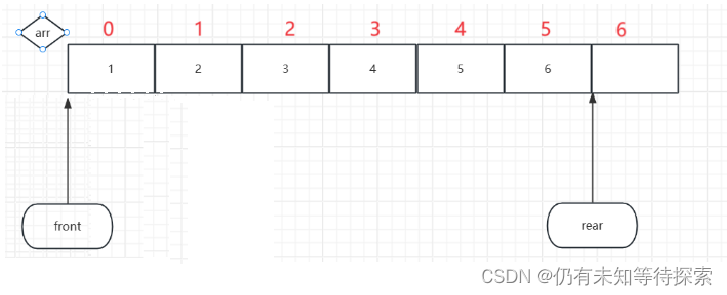
假设这是一个队列(并且装满了,一般队列填数组会空一个元素位置)。
如果进行一次出队操作。
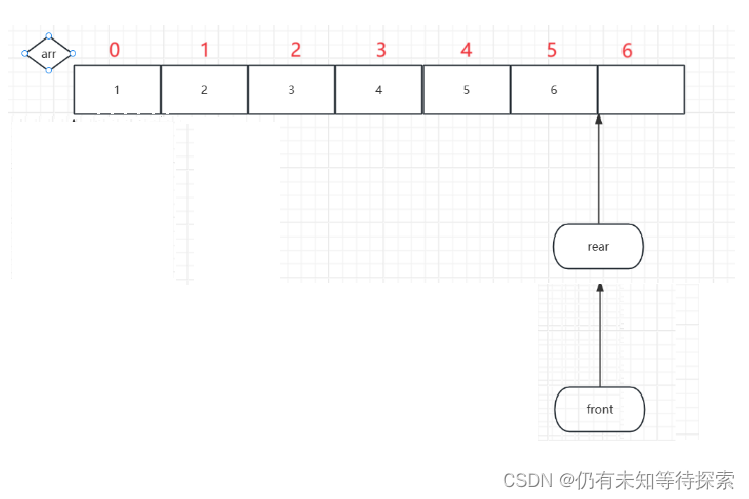
如果要进行一次入队操作的话,现在只有下标为0的地方有空,但是现在rear指向的是最后一个元素的下一个元素。如果rear继续+1,往下走的话,数组会越界,只有让rear指向下标为零的位置上。
3、循环队的创建及其初始化
第一种写法
- 创建循环队和创建栈的操作大体相同,都是用malloc进行开辟空间,如果失败,则返回空。
- 在对front指针和rear指针进行初始化的时候,将他们赋值为0就完成了操作。(这里说的指针是泛称,不是真的指针类型,而是有着和指针相同的作用,都用来记录位置)
#include<stdio.h>
#include<stdlib.h>
#define MAX 100
typedef int elemtype;
typedef struct Queue
{
//第一种写法
elemtype data[MAX];//elemtype是为了改data的数据类型的时候方便
int front;//队首指针
int rear;//队尾指针
}Queue;
Queue* CreateQueue();
int main()
{
Queue* Q = CreateQueue();
if (Q == NULL)//如果Q开辟失败,结束程序
{
return 0;
}
return 0;
}
Queue* CreateQueue()
{
Queue* Q = (Queue*)malloc(sizeof(Queue));
if (Q == NULL)
{
perror("malloc");//写出错误原因
return NULL;//如果Q开辟失败,提前结束
}
Q->front = 0;
Q->rear = 0;
return Q;
}第二种写法
大体上和第一种写法没什么区别,唯一不同的是还要在给数组data开辟空间。
#include<stdio.h>
#include<stdlib.h>
#define MAX 100
typedef int elemtype;
typedef struct Queue
{
//第二种写法
elemtype* data;
int front;//队首指针
int rear;//队尾指针
}Queue;
Queue* CreateQueue();
int main()
{
Queue* Q = CreateQueue();
if (Q == NULL)
{
return 0;
}
return 0;
}
Queue* CreateQueue()
{
Queue* Q = (Queue*)malloc(sizeof(Queue));
if (Q == NULL)
{
perror("malloc_Q");
return NULL;
}
Q->data = (elemtype*)malloc(MAX * sizeof(elemtype));
if(Q->data==NULL)
{
perror("malloc_Q->data");
return NULL;
}
Q->front = 0;
Q->rear = 0;
return Q;
}
4、 判断队满
当Q->front == (Q->rear + 1) % MAX的时候,队满。
Q->front=0,Q->rear=6,将这数据带入上述式子,可得出队满结论,和实际符合。其中主要取循环作用的是取余号(%)。
当队满的时候返回1,不满返回0。
int IsFull(Queue* Q)
{
if (Q->front == (Q->rear + 1) % MAX)
return 1;
return 0;
}5、判断队空
当Q->front == Q->rear的时候,队空。
当对空的时候返回1,否则返回0。
int IsEmpty(Queue* Q)
{
if (Q->front == Q->rear)
return 1;
return 0;
}6、入队
注意: Q->rear = (Q->rear + 1) % MAX
int Push(Queue* Q, elemtype x)
{
if (IsFull(Q))
{
return 0;
}
Q->data[Q->rear] = x;
Q->rear = (Q->rear + 1) % MAX;
return 1;
}7、出队
注意: Q->front= (Q->front + 1) % MAX
int Pop(Queue* Q, elemtype* x)
{
if (IsEmpty(Q))
{
return 0;
}
*x = Q->data[Q->front];
Q->front = (Q->front + 1) % MAX;
return 1;
}8、求长度
注意:有可能Q->rear会在Q->front的左边。
int Queue_length(Queue* Q)
{
return (Q->rear - Q->front + MAX) % MAX;
}三、优势
以上所有的操作的时间复杂度均为O(1) 。
四、总代码
#include<stdio.h>
#include<stdlib.h>
#define MAX 100
typedef int elemtype;
typedef struct Queue
{
//第一种写法
elemtype data[MAX];//elemtype是为了改data的数据类型的时候方便
int front;//队首指针
int rear;//队尾指针
}Queue;
Queue* CreateQueue();
int IsFull(Queue* Q);
int IsEmpty(Queue* Q);
int Push(Queue* Q, elemtype x);
int Pop(Queue* Q, elemtype* x);
int Queue_length(Queue* Q);
int main()
{
Queue* Q = CreateQueue();
if (Q == NULL)
{
return 0;
}
for (int i = 0; i < 3; i++)
{
int ret = Push(Q, i);
if (ret == 0)
{
printf("队满,入队失败\n");
}
else
{
printf("入队成功\n");
}
}
int x;
int ret = Pop(Q, &x);
if (ret == 0)
{
printf("队满,入队失败\n");
}
else
{
printf("出队成功\n");
}
return 0;
}
Queue* CreateQueue()
{
Queue* Q = (Queue*)malloc(sizeof(Queue));
if (Q == NULL)
{
perror("malloc");
return NULL;
}
Q->front = 0;
Q->rear = 0;
return Q;
}
int IsFull(Queue* Q)
{
if (Q->front == (Q->rear + 1) % MAX)
return 1;
return 0;
}
int IsEmpty(Queue* Q)
{
if (Q->front == Q->rear)
return 1;
return 0;
}
int Push(Queue* Q, elemtype x)
{
if (IsFull(Q))
{
return 0;
}
Q->data[Q->rear] = x;
Q->rear = (Q->rear + 1) % MAX;
return 1;
}
int Pop(Queue* Q, elemtype* x)
{
if (IsEmpty(Q))
{
return 0;
}
*x = Q->data[Q->front];
Q->front = (Q->front + 1) % MAX;
return 1;
}
int Queue_length(Queue* Q)
{
return (Q->rear - Q->front + MAX) % MAX;
}谢谢大家的支持!