GoogLeNet是google推出的基于Inception模块的深度神经网络模型，在2014年的ImageNet竞赛中夺得了冠军，在随后的两年中一直在改进，形成了Inception V2、Inception V3、Inception V4等版本。

Inception块

4个路径从不同层面抽取信息，然后在输出通道维合并。

$1\times 1$卷积可以看作是用来降低通道数，控制模型复杂度的。

与单$3\times 3$或$5\times 5$卷积层相比，Inception块有更少的参数个数和计算复杂度。

• Inception-BN（V2），使用batch normalization

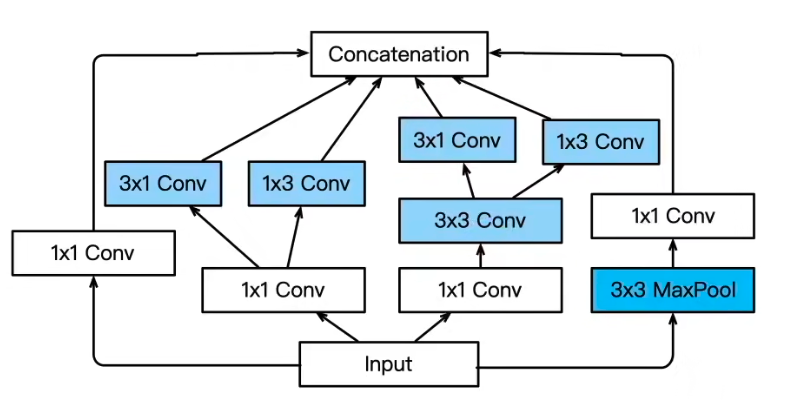
• Inception-V3，修改了Inception块

  • 替换$5\times 5$为多个$3\times 3$卷积层

  • 替换$5\times 5$为$1\times 7$和$7\times 1$卷积层

  • 替换$3\times 3$为$1\times 3$和$3\times 1$卷积层

  • 更深

• Inception-V4，使用残差连接

V3，消耗内存较多，速度较慢，但精度比较好。

段3

段4

段5

总结：

Inception块用4条有不同超参数的卷积层和池化层的路来抽取不同的信息，它的一个主要优点是模型参数小，计算复杂度低。

GoogleNet使用了9个Inception块，是第一个达到上百层的网络。