1、极大似然法（ maximum likelihood estimation，MLE ）

极大似然法（ maximum likelihood estimation，MLE ）是概率统计中估算模型参数的一种很经典和重要的方法。
（1）定义
最大似然估计是一种基于观测数据估计概率模型参数的统计方法。最大似然函数的目标是找到最大似然函数的参数值集，该函数测量在假设模型下观察给定数据的概率。
（2）MLE关键组成部分

• Likelihood Function似然函数
  
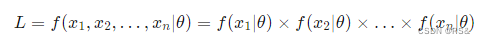
• Log-Likelihood Function对数似然函数
• MLE Objective目标函数

2、最小二乘算法

最小二乘问题的四种解法——牛顿法，梯度下降法，高斯牛顿法和列文伯格-马夸特法Levenberg-Marquardt（LM）。
最小二乘问题的四种解法——牛顿法，梯度下降法，高斯牛顿法和列文伯格-马夸特法的区别和联系

2.1 牛顿法

2.2 梯度下降法

2.3 高斯牛顿法

2.4 列文伯格-马夸特法Levenberg-Marquardt（LM）

参考资料：
https://blog.csdn.net/liu14lang/article/details/53991897
Levenberg-Marquardt（列文伯格-马夸尔特）算法
机器学习-最小二乘拟合
GitHub：https://github.com/abnerbog/levenberg-marquardt-method
GitHub：https://github.com/fabiodimarco/tf-levenberg-marquardt

（1）定义
莱文贝格－马夸特方法（Levenberg–Marquardt algorithm）能提供数非线性最小化（局部最小）的数值解，是利用梯度求最大（小）值的算法。
（2）优点
LM算法是介于牛顿法与梯度下降法之间的一种非线性优化方法，对于过参数化问题不敏感，能有效处理冗余参数问题，使代价函数陷入局部极小值的机会大大减小，这些特性使得LM算法在计算机视觉等领域得到广泛应用。

参考资料：

1、Understanding Maximum Likelihood Estimation (MLE) in Machine Learning：https://rmoklesur.medium.com/understanding-maximum-likelihood-estimation-mle-in-machine-learning-6d69c8fec53
2、Maximum Likelihood Estimation (MLE)：https://brilliant.org/wiki/maximum-likelihood-estimation-mle/
3、Python Guide To Maximum Likelihood Estimation：https://analyticsindiamag.com/maximum-likelihood-estimation-python-guide/
4、GITHUB levenberg-marquardt-method：https://github.com/abnerbog/levenberg-marquardt-method