C++：哈希

news2024/11/16 1:29:08

目录

一、unordered系列关联容器

二、底层的结构

哈希结构

哈希冲突/哈希碰撞

①、闭散列 —> 开放定址法

闭散列的模拟实现

②、开散列 —> 拉链法/哈希桶

哈希桶的模拟实现

三、哈希应用

位图

位图的特点

位图的模拟实现

布隆过滤器

布隆过滤器的模拟实现

一、unordered系列关联容器

unordered_set

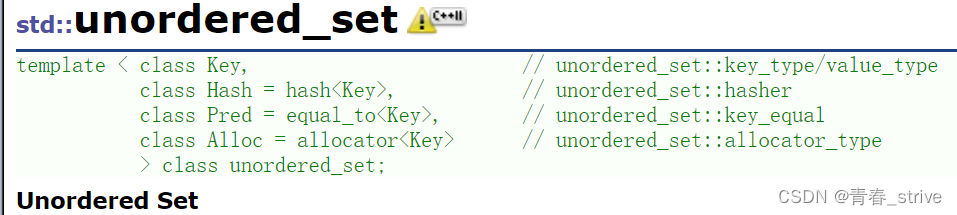
unordered_map

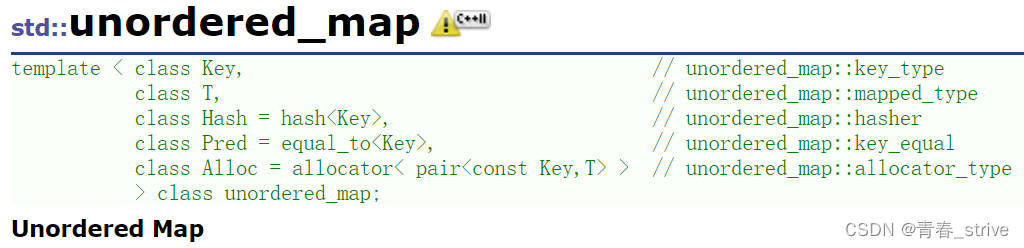
而关于unordered_set和unordered_map与map和set的用法区别不大，具体用法看map和set部分的详解

unordered_set和unordered_map与map和set主要有以下两个区别：

1、map和set遍历是有序的，而unordered_set和unordered_map遍历是无序的

2、map和set是双向迭代器，而unordered_set和unordered_map是单向迭代器

而引进unordered系列的原因是因为：在大量数据的情况下，增删查改效率更高，尤其是查效率最高

下面演示一下用法：

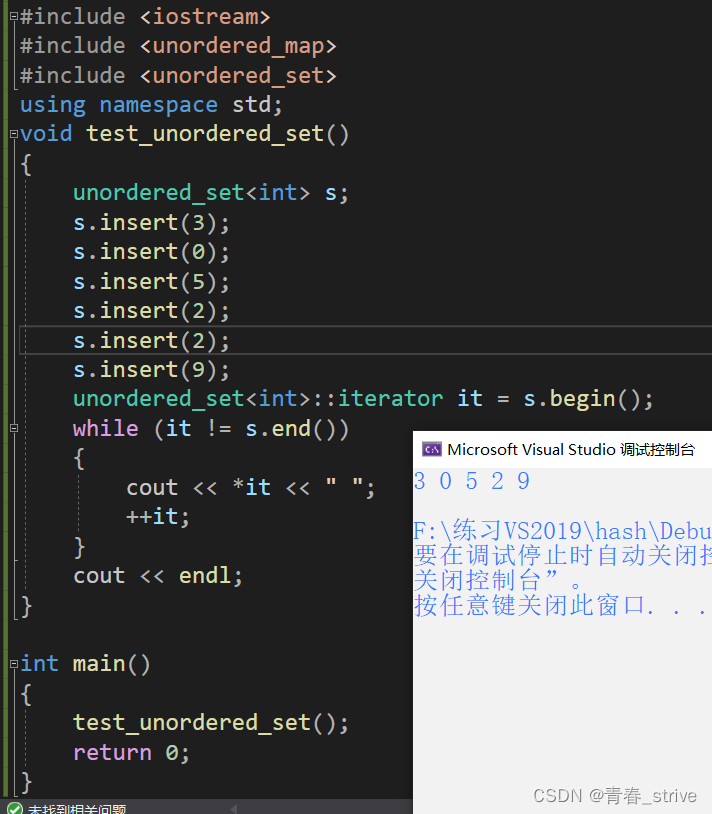
通过结果可以看出unordered_set插入后是无序的，unordered_set与set的用法基本相同，也是有去重的作用，剩下用法参照map和set

二、底层的结构

哈希结构

哈希也叫散列，表示值跟存储位置建立映射关联关系

在我们还没学习哈希时，做题时也用过类似哈希的思路去解决问题，比如说要查找一个数组中唯一只出现一次的数字

这时我们只需要遍历一遍数组，遍历到每一个数字时，在一个新数组的对应位置++，最后再遍历一遍新数组，看哪个位置的值为1，该位置所对应的数字即为只出现一次的数字

但是有时候会出现特殊情况，比如只有极少个数的数，但是它们之间的差距却很大，如果我们开辟与之对应位置的数组，就会导致非常浪费空间，这时就出现了哈希的除留余数法的思想

哈希中构造出来的结构：哈希表(散列表)，就类比于上面使用的数组

除留余数法：散列表是大小为n的，用这个几个大小不同的数，分别去模p(%np)，这里的p是最接近n或等于n的质数，之后再存入散列表中，这就是除留余数法，即Hash(i) = i % p(p <= n)这时无论是多大的数，都可以存在这个空间中，也不怕开辟太多的多余空间，造成空间浪费

例如：有,四个数,7,201,400，40000，这时我们用除留余数法的思想，假设有一个大小为5的散列表，接下来这,四个数分别%5，得到的结果是2，1，0，0，就可以很好地存储进散列表中了，不用像之前一样开辟40000个空间却只存4个数而造成空间浪费

这时又有问题了，四个数中的400与40000%5后都是0，那怎么解决呢？

这种情况就叫做哈希冲突/哈希碰撞

哈希冲突/哈希碰撞

有两种方法解决哈希碰撞/哈希冲突：

①、闭散列 —> 开放定址法

开放定址法即如果当前位置已经被占用了，那我们就接着往后面找，有没有没有被占用的的位置

而开放定址法也有两种方式：

第一种：线性探测

线性探测就是指一个位置被占用后，就依次往后找没被占用的位置

但是有可能会出现，位置依次占用后，如果删除一个位置的数据，接下来在找后面的数据时，会因为删除的位置为空而找不到了，所以我们可以用枚举设置一个状态，(EMPTY)空、(EXIST)存在、(DELETE)删除，这样删除完后，如果后面数据发现此位置为空， 但是状态是删除时，就不会终止查找了

哈希在扩容时引入了负载因子(载荷因子)的概念：

负载因子 = 填入表中元素个数 / 散列表的长度

负载因子越大，冲突概率越大；负载因子越小，冲突概率越小

一旦到了负载因子的基准值，就需要扩容了

基准值越大，冲突越多，效率越低，空间利用率越高

基准值越小，冲突越少，效率越高，空间利用率越低

一般基准值是控制在0.7~0.8

 但是线性探测在一些特殊情况下，就会显得非常不好：

比如某一个位置非常冲突，连续几个数都要这个位置，所以都会向后延伸，这时如果再遇到该位置后面位置的数，依然还得往后延伸，因此会造成某个位置冲突很多的情况下，互相占用，冲突一片，下面的二次探测能够稍微减轻冲突的情况

第二种：二次探测

线性探测是一个数所对应的位置如果有数了，就+i处理，即+1到下一个位置，如果下一个位置还有数+2，以此类推（i >= 0）

而二次探测则是+ i^2（i >= 0）

会比线性探测好一点，但是本质依然可能会互相占用概率大，这两种方法统一的弊端就是，例如：好几个数据都在一号位置存，那么就顺延到后面位置存，而后面数据存的时候发现自己的位置被占用，就又会占用其他数据的位置，恶性循环

下面有一种更好的方式就叫做拉链法/哈希桶，很好解决了上面的问题

闭散列的模拟实现
//设置状态，表示空、存在、删除
enum State
{
	EMPTY,
	EXIST,
	DELETE
};

//有一个状态_state以及一个pair类型的数据_kv
template<class K, class V>
struct HashData
{
	pair<K, V> _kv;
	State _state = EMPTY;
};

//这个是正常能取模的数据调用的
template<class K>
struct HashUsual
{
	size_t operator()(const K& key)
	{
		return (size_t)key;
	}
};

//有些数据不能直接取模，例如string，需要自己写仿函数
//也可以不主动调用，特化处理
template<>
struct HashUsual<string>
{
	//string类型的就返回所有字符的ascll码
	size_t operator()(const string& key)
	{
		size_t val = 0;
		for (auto& e : key)
		{
			val += e;
		}

		return val;
	}
};

template<class K, class V, class Hash = HashUsual<K>>
class HashTable
{
public:
	bool Insert(const pair<K, V>& kv)
	{
		//负载因子到了就扩容，一般是0.7~0.8
		//之所以>=7，不是>=0.7，是因为两个整数除完不能等于0.7这个小数
		//所以干脆放大十倍就不会有这个问题了
		if (_table.size() == 0 || 10 * _size / _table.size() >= 7)
		{
			size_t newsize = _table.size() == 0 ? 10 : _table.size() * 2;
			HashTable<K, V> newHT;
			newHT._table.resize(newsize);
			//旧表的数据映射到新表中
			for (auto& e : _table)
			{
				if (e._state == EXIST)
				{
					newHT.Insert(e._kv);
				}
			}
			//旧表与新表交换，执行完毕旧表自动释放了
			_table.swap(newHT._table);
		}
		//线性探测
		Hash hs;
		//找到要存储的位置hashi
		size_t hashi = hs(kv.first) % _table.size();
		
		while (_table[hashi]._state == EXIST)
		{
			hashi++;
			//超过散列表的范围后，需要返回到开头
			hashi %= _table.size();
		}
		_table[hashi]._kv = kv;
		_table[hashi]._state = EXIST;
		++_size;

	//	//二次探测
	//	Hash hs;
	//	//找到要存储的位置start
	//	size_t start = hs(kv.first) % _table.size();
	//	size_t i = 0;
	//	size_t hashi = start;
	//	while (_table[hashi]._state == EXIST)
	//	{
	//		//如果_table[hashi]有值，hashi就+i^2
	//		i++;
	//		hashi = start + i * i;
	//		hashi %= _table.size();
	//	}
	//	_table[hashi]._kv = kv;
	//	_table[hashi]._state = EXIST;
	//	++_size;

		return true;
	}


	HashData<K, V>* Find(const K& key)
	{
		//如果表为空，就不查找了
		if (_table.size() == 0)
		{
			return nullptr;
		}
		Hash hs;
		//除留余数法
		size_t hashi = hs(key) % _table.size();
		while (_table[hashi]._state != EMPTY)
		{
			if (_table[hashi]._state != DELETE && _table[hashi]._kv.first == key)
			{
				return &_table[hashi];
			}

			hashi++;
			//如果超过散列表，就回到开头
			hashi %= _table.size();
			//如果回到开头了，就break
			if (hashi == key % _table.size())
			{
				break;
			}
		}

		return nullptr;
	}

	bool Erase(const K& key)
	{
		//查找值为key的数据在不在
		//如果在，只需要改变状态再--_size就完成了删除
		HashData<K, V>* ret = Find(key);
		if (ret)
		{
			ret->_state = DELETE;
			--_size;
			return true;
		}
		else
		{
			return false;
		}
	}

	void Print()
	{
		for (size_t i = 0; i < _table.size(); ++i)
		{
			if (_table[i]._state == EXIST)
			{
				printf("[%d:%d] ", i, _table[i]._kv.first);
			}
			else
			{
				printf("[%d:×] ",i);
			}
		}
	}
private:

	//存储的每个数据是HashData<K, V>的
	vector<HashData<K, V>> _table;
	size_t _size = 0;//表示数组中存储了多少有效数据
};

void testHT()
{
	HashTable<int, int> ht;
	int arr[] = { 3,6,15,13,27,48 };
	for (auto e : arr)
	{
		ht.Insert(make_pair(e, e));
	}
	
	ht.Print();
}
②、开散列 —> 拉链法/哈希桶

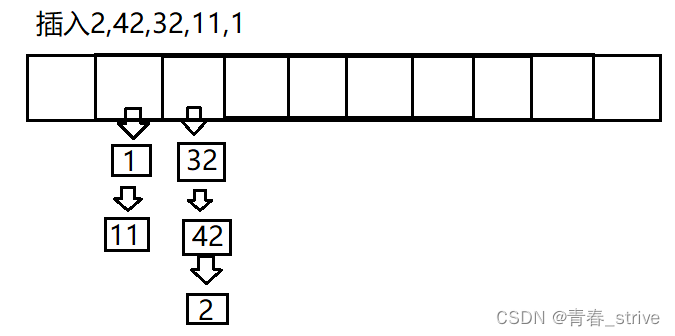
哈希桶的方式，就是如果数据在一个位置，就先挂起，先不放入位置中

哈希桶的表就不是普通数组了，而是指针数组

每次插入新的数据时，只需要头插即可

例如下图所示方式： 

哈希桶的模拟实现
template<class K,class V>
struct HashNode
{
	pair<K, V> _kv;
	HashNode<K, V>* _next;

	HashNode(const pair<K,V>& kv)
		:_kv(kv)
		,_next(nullptr)
	{}
};

//这个是正常能取模的数据调用的
template<class K>
struct HashUsual
{
	size_t operator()(const K& key)
	{
		return (size_t)key;
	}
};

//有些数据不能直接取模，例如string，需要自己写仿函数
//也可以不主动调用，特化处理
template<>
struct HashUsual<string>
{
	//string类型的就返回所有字符的ascll码
	size_t operator()(const string& key)
	{
		//BKDR法
		size_t val = 0;
		for (auto& e : key)
		{
			val *= 131;
			val += e;
		}

		return val;
	}
};


template<class K,class V,class Hash = HashUsual<K>>
class HashTable
{
	typedef HashNode<K, V> Node;
public:
	//析构，释放哈希桶
	~HashTable()
	{
		for (size_t i = 0; i < _table.size(); ++i)
		{
			Node* cur = _table[i];
			while (cur)
			{
				//记录cur的next
				Node* next = cur->_next;
				delete cur;
				cur = next;
			}
			//置空
			_table[i] = nullptr;
		}
	}

	bool Insert(const pair<K, V>& kv)
	{
		//去重
		if (Find(kv.first))
		{
			return false;
		}
		Hash hs;//仿函数
		//负载因子到1就扩容
		if (_size == _table.size())
		{
			size_t newsize = _table.size() == 0 ? 10 : _table.size() * 2;
			vector<Node*> newtable;
			newtable.resize(newsize, nullptr);

			//旧表结点映射到新表
			for (size_t i = 0; i < newtable.size(); ++i)
			{
				Node* cur = _table[i];
				while (cur)
				{
					//提前保存cur的next，下面会改变next，不然会找不到
					Node* next = cur->_next;

					size_t hashi = hs(cur->_kv.first) % newtable.size();
					//头插：插入结点的next指向新表结点的第一个
					//插入结点作为新表结点的第一个
					cur->_next = newtable[hashi];
					newtable[hashi] = cur;
				}
				_table[i] = nullptr;
			}
			//交换_table与newtable,便于运行结束自动删除_table
			_table.swap(newtable);
		}
		

		size_t hashi = hs(kv.first) % _table.size();
		//头插
		Node* newnode = new Node(kv);
		newnode->_next = _table[hashi];
		_table[hashi] = newnode;
		++_size;

		return true;
	}

	Node* Find(const K& key)
	{
		//如果表中无数据，直接return
		if (_table.size() == 0)
		{
			return nullptr;
		}
		Hash hs;//仿函数
		//找到要查找数据对应的位置
		size_t hashi = hs(key) % _table.size();
		Node* cur = _table[hashi];
		//在该位置挂起的数据中找
		while (cur)
		{
			if (cur->_kv.first == key)
			{
				return cur;
			}
			cur = cur->_next;
		}
		//如果代码走到这里，说明没找到
		return nullptr;
	}

	bool Erase(const K& key)
	{
		//如果为空，直接return
		if (_table.size() == 0)
		{
			return nullptr;
		}
		Hash hs;//仿函数
		size_t hashi = hs(key)% _table.size();
		Node* cur = _table[hashi];
		Node* prev = nullptr;
		while (cur)
		{
			//如果相等则删除
			if (cur->_kv.first == key)
			{
				//删除的是_table[hashi]的头结点
				if (prev == nullptr)
				{
					_table[hashi] = cur->_next;
				}
				//删除的是_table[hashi]的中间结点
				else
				{
					prev->_next = cur->_next;
				}
				delete cur;
				--_size;	

				return true;
			}
			prev = cur;
			cur = cur->_next;
		}
		//代码运行到这里，说明没有找到
		return false;
	}

private:
	vector<Node*> _table;
	size_t _size = 0;//存储的有效数据个数	
};

三、哈希应用

位图

有一道题来引出位图的概念：

假设给40亿个不重复且未排序的无符号整数，然后给出一个无符号整数，如何快速判断这个数是否在这40亿个数中？

我们的之前学习过的方法例如：堆、搜索树、哈希这些方法确实搜索的速度很快，但是一个无符号整数4个字节，40亿个无符号整数存储空间得占用160亿个字节即大约14GB左右，这肯定是存不下的，只能存在磁盘中，而磁盘查找又很麻烦，效率非常低，所以之前学习的方法是没有办法解决的 

这里就引入位图的概念，在给的这40亿个无符号整数，给定的一个无符号整数只会有两种状态，在或者不在，那么就可以使用二进制的比特位0/1存储(1表示在，0表示不在)

因为1GB = 1024MB = 1024 * 1024KB = 1024 * 1024 * 1024 byte约等于10亿，所以40亿字节相当于4GB，而40亿大约是2^32，现在使用位图用的是40亿个比特位，一个byte = 8个比特位，所以位图占用的空间就是4GB / 8 约等于512MB，对比上面所占的空间，可以说是非常小了，效率也很快

而通过上面的例子，就可以得知，位图就是用每一位来存在某种状态，是用于非常大的数据，且数据无重复的情况，通常是判断某个数据存不存在

而这2^32比特位我们应该怎么开辟呢，就开辟每个元素是char类型的数组即可，一个char是8个比特位，所以就相当于每8个比特位用一个char存储，即0~7位存储在第一个char，8~15存储在第二个char，以此类推

这时我们通过/8和%8就分别可以得知在第几个char与在这个char的第几个比特位

例如前两个char表示的比特位分别是0~7和8~15，那么假设数字10，10 / 8 == 1，10 % 8 == 2，所以数字10就在第一个char的第二个比特位上（注意是从0开始的），如下所示：

而不论是多少数据，并不是说题目给10亿数据，我们就开10亿个比特位大小的空间，而是不论是10亿，50亿，90亿，我们都开整数的最大值，即42亿9千万多，因为给出的数据是无序的，不能保证数据的大小

所以开辟时可以有下面的方式：

bit_set<-1>：可以传-1，是因为位图的非类型模板参数是size_t类型的，即无符号整型，-1表示的就是整型的最大值

bit_set<0xffffffff>：0xffffffff是用8个16进制位表示的，1个16进制位等于4个2进制位，所以8个16进制位都是f，就表示二进制位都为1，也是整型的最大值

我们上面也计算了开辟整型的最大值也就是42亿多比特位，算下来就是512MB左右，下面可以看看实际的情况是不是我们所说的那样：

先用上面的方法创建整型最大值个比特位，然后打断点调试：

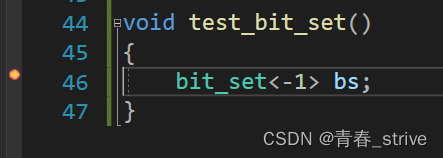
这时打开我们的Windows任务管理器，发现此时运行的这个进程所占内存是0.5MB：

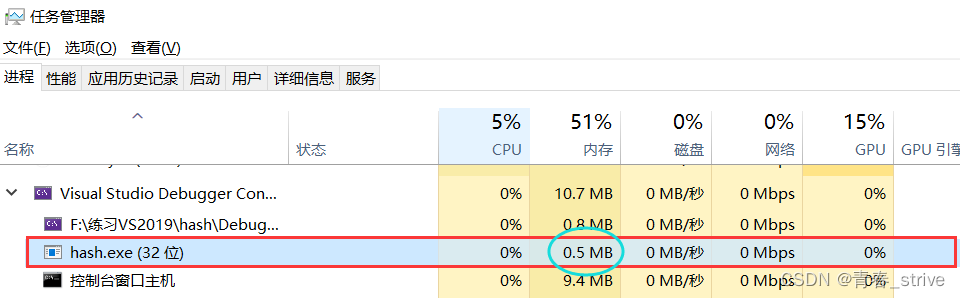
接下来我们按F10，创建这个bs变量即开辟好整型的最大值个比特位的空间（箭头表示已经走到的位置，说明创建完成了）：

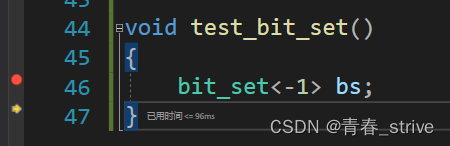
这时再打开任务管理器：

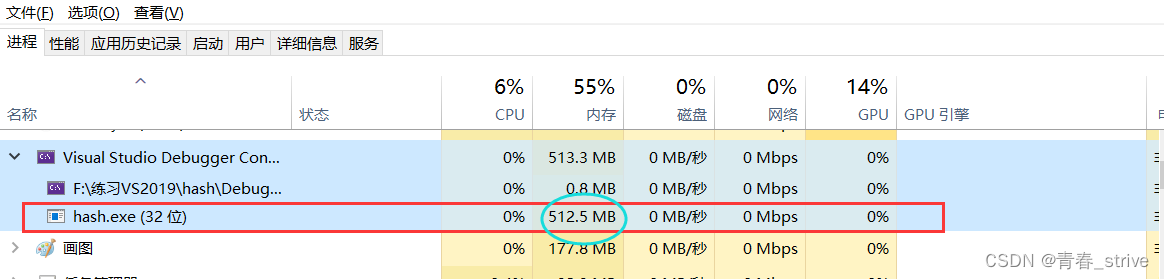
可以清楚看到此时该进程所占用的内存变为了512MB

位图的特点

1、快，且节省空间（512MB左右）

2、比较局限，只能映射整型（因为对应比特位的下标都是整数）

位图是直接定址法，不存在冲突

位图的模拟实现

bitset是C++库中的容器，我们只实现了最核心的三个接口：set、reset、test

set：将一个数对应的比特位变为1

reset：将一个数对应的比特位变为0

test：测试一个数存在不存在

//非类型模板参数
template<size_t N>
class bitset
{
public:
	bitset()
	{
		//每次多开一个char，保证所有数据都能存进入
		//默认所有位初始化为0
		_bits.resize(N / 8 + 1, 0);
	}

	//下面的i都表示在第几个char中的比特位中
	//下面的j都表示在这个char的第几个比特位上
	void set(size_t x)
	{
		size_t i = x / 8;
		size_t j = x % 8;
		//算出的比特位按位与1，该位置就为1了
		_bits[i] |= (1 << j);
	}

	void reset(size_t x)
	{
		size_t i = x / 8;
		size_t j = x % 8;
		//~是按位取反，每一位都0变1,1变0
		_bits[i] &= ~(1 << j);
	}

	bool test(size_t x)
	{
		size_t i = x / 8;
		size_t j = x % 8;

		return _bits[i] & (1 << j);
	}
private:
	vector<char> _bits;
};

void test_bitset()
{
	bitset<-1> bs;
}

布隆过滤器

上面所说的位图只能处理整数，而如果是其他类型的例如字符串之类的就不能处理了，所以这里引入了布隆过滤器

布隆过滤器设计思路：就是将字符串使用字符串哈希算法转换成整型，然后去映射一个位置进行标记

但是这样实现，会造成误判的情况，比如说有两个字符串完全不同，但是使用字符串哈希算法转换成的整型数值却是一样的，从而造成误判

而误判只会存在于在的情况，因为有一个字符串映射到a位置，而另一个字符串本身没有出现，但是经过算法算出来的值与上一个字符串相同，这时这个字符串存在的情况就会出现误判

而字符串不存在的情况是不会有误判的情况出现的，因为如果该位置映射的值为0，那么就说明肯定没有对应该位置的字符串出现，所以也就不存在误判的事情了

对于上面误判的情况，我们可以加以改进，可以将一个字符串多映射几个位置，这样就可以有效降低误判率，因为一个字符串所映射的一个位置和另一个字符串映射的位置重复了，那再与该字符串映射的其他位置同样重复的情况的可能性就很小了，所以可以有效降低误判率

我们知道：一个值映射的位越多，误判的概率就越低，但是映射的位如果太多，那么空间的消耗也就会越多

我们一般选择映射3个位置

而布隆过滤器的使用场景如果允许误判的情况，例如游戏中给角色起名时，将已经存在的名称存在布隆过滤器中，这样新用户起名时，如果存在，告知用户存在，如果不存在，就起名成功，效率是非常高的

而如果有场景不允许存在误判，那么就多一个步骤，如果存在布隆过滤器中，就去数据库中查找，确认在或不在，而如果不在布隆过滤器中，那就肯定不在，就不需要再去数据库中查找，也可以有效的提高效率

布隆过滤器的模拟实现

//N表示映射N个值，Hash1/2/3表示仿函数，即使用三种不同方式映射到不同地址
template<size_t N, class K, class Hash1, class Hash2, class Hash3>
class BloomFilter
{
public:
	void Set(const K& key)
	{
		size_t hash1 = hash1()(key) % _ratio * N;
		_bits.set(hash1);

		size_t hash2 = hash2()(key) % _ratio * N;
		_bits.set(hash2);

		size_t hash3 = hash3()(key) % _ratio * N;
		_bits.set(hash3);
	}

	void Test(const K& key)
	{
		//验证该位置是否存在时，因为一个值映射三个位置
		//所以不能一个位置满足就当做存在
		//是需要判断这三个位置是否都不存在
		//直到三个位置都判断之后才结束，才return true
		//虽然有误判率，但是误判率也是很小的
		size_t hash1 = hash1()(key) % (_ratio * N);
		if (!_bits.set(hash1))
			return false; //准确判断

		size_t hash2 = hash2()(key) % (_ratio * N);
		if (!_bits.set(hash2))
			return false; //准确判断

		size_t hash3 = hash3()(key) % (_ratio * N);
		if (!_bits.set(hash3))
			return false; //准确判断

		return true;      //可能误判
	}
private:
	//这里的_ratio是使用公式大致算出来，在三个哈希函数时
	//需要多给大约5个比特位存储
	//所以N个数据，就开辟_ratio*N个空间
	const static size_t _ratio = 5;
	bitset<_ratio* N> _bits;
};

而关于布隆过滤器的删除操作，也就是reset，是不太建议的，因为一个数据可以对应多个位置，如果有两个数据对应了同一个位置，想删除一个，另一个也就被删除了

想解决这种问题，只能给每个位置在设置一个值，表示有几个数据映射到这个位置，删除一个数据就--，这样就不会有上面的问题了，但是这样相当于原本每个位置用一个比特位存储，现在每个位置又多了一个字节存储映射该位置的次数，这与布隆过滤器的初衷相违背了，本来布隆过滤器的优势就是空间占用小，效率高，这样空间也变大了，效率也低了，所以一般我们是不考虑删除操作的

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1131210.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

ubuntu 安装串口工具和添加虚拟串口

ubuntu 安装串口工具和添加虚拟串口

目录 一、串口工具安装 二、使用Windows本身虚拟的串口 &#xff08;一&#xff09;添加串口 1、保证虚拟机是关闭状态&#xff0c;打开“虚拟机设置”&#xff0c;点击“添加”。 2、选中“串行端口”&#xff0c;点击“完成”。 3、选中刚添加的串口&#xff0c;下拉选…
阅读更多...
XXXSpringMVC“框架的简单创建与使用，快速上手；

XXXSpringMVC“框架的简单创建与使用，快速上手；

前言 【描述】 " 【环境】 系统"Windows"&#xff0c;软件"IntelliJ IDEA 2021.1.3(Ultimate Edition)"&#xff1b;“Java版本"1.8.0_202”&#xff0c;“Spring"版本"2.5.9”&#xff1b; 实操 【实操1】 说明 【描述】 创建&quo…
阅读更多...
大学生学习新途径：视频号视频下载助你获取学术资源

大学生学习新途径：视频号视频下载助你获取学术资源

​在这个信息爆炸的时代&#xff0c;大学生们为了获取更多的学术资源常常面临诸多挑战。然而&#xff0c;随着互联网的发展&#xff0c;视频号平台逐渐成为了学生们学习的新途径。本文将介绍如何通过视频号视频下载来获取学术资源&#xff0c;帮助大学生们更好地学习。 1. 视频…
阅读更多...
测试内容总结

测试内容总结

目录 面试题类型 测试用例 非软件题型 软件类型 代码题型 关于个人的项目设计测试类型 万能公式 自动化面试 什么是自动化以及为什么要做 selenium驱动浏览器的工作原理 设计自动化测试的思路(个人的自动化亮点) 1、明确个人项目里哪些页面需要做web做自动化测试—…
阅读更多...
FreeRTOS 消息队列 详解

FreeRTOS 消息队列 详解

目录 什么是队列&#xff1f; 消息队列特点 1. 数据入队出队方式 2. 数据传递方式 3. 多任务访问 4. 出队、入队阻塞 消息队列相关 API 函数 1. 创建队列 2. 写队列 3. 读队列 消息队列实操 什么是队列&#xff1f; 队列又称消息队列&#xff0c;是一种常用于任务间…
阅读更多...
SpringBoot+SpringMVC+MybatisPlus

SpringBoot+SpringMVC+MybatisPlus

文章目录 SpringBootSpringMVCMybatisPlus怎样在SpringBoot中引入SpringMVC?首先看下引入的依赖创建数据库表创建DO类创建MyBatisPlus动态代理接口创建controller控制器接收http请求创建SpringBoot配置文件application.yml最后创建启动类 SpringBootSpringMVCMybatisPlus 怎样…
阅读更多...
管理Secrets

管理Secrets

使用 kubectl 管理 Secret 创建 Secret Secret 对象用来存储敏感数据&#xff0c;如 Pod 用于访问服务的凭据。例如&#xff0c;为访问数据库&#xff0c;你可能需要一个 Secret 来存储所需的用户名及密码。 使用原始数据 kubectl create secret generic db-user-pass \--from…
阅读更多...
【字符串】【将字符数组转为字符串】Leetcode 122 路径加密

【字符串】【将字符数组转为字符串】Leetcode 122 路径加密

【将字符数组转为字符串】Leetcode 122 路径加密 解法1 在Java中&#xff0c;char数组没有直接的toString()方法来将其转换为字符串。如果你想将char数组转换为字符串&#xff0c;可以使用String类的构造函数来实现&#xff1a; ⭐️⭐️⭐️⭐️⭐️⭐️⭐️⭐️⭐️⭐️⭐️⭐…
阅读更多...
使用vue3 搭建一个H5手机端访问的项目

使用vue3 搭建一个H5手机端访问的项目

首先说明&#xff0c;我本地之前运行过vue的项目&#xff0c;所以具有一些基础的运行环境&#xff0c;这里直接按步骤讲我项目框架搭建的过程。 这个不建议使用驼峰&#xff0c;按规范单词中间加横杠就可以。一般会出现选择项&#xff0c;按方向键选择&#xff0c;我这边选择了…
阅读更多...
MS COCO数据集的评价标准以及不同指标的选择推荐（AP、mAP、MS COCO、AR、@、0.5、0.75、1、目标检测、评价指标）

MS COCO数据集的评价标准以及不同指标的选择推荐（AP、mAP、MS COCO、AR、@、0.5、0.75、1、目标检测、评价指标）

目标检测模型性能衡量指标、MS COCO 数据集的评价标准以及不同指标的选择推荐 0. 引言 0.1 COCO 数据集评价指标 目标检测模型通过 pycocotools 在验证集上会得到 COCO 的评价列表&#xff0c;具体参数的含义是什么呢&#xff1f; 0.2 目标检测领域常用的公开数据集 PASCAL …
阅读更多...
【23真题】招600+，太火爆！题目略难！快来挑战！

【23真题】招600+，太火爆！题目略难！快来挑战！

今天分享的是23年重庆邮电大学801的信号与系统试题及解析。 本套试难度分析&#xff1a;22年重庆邮电大学801考研真题我也发布过&#xff0c;如有需要戳这里自取&#xff01;本套试题内容难度中等偏上&#xff0c;没有选择计算题&#xff0c;涉及的知识点较多&#xff0c;题量…
阅读更多...
干洗店软件，洗鞋店软件小程序，洗衣收银系统，洗衣工厂系统；

干洗店软件，洗鞋店软件小程序，洗衣收银系统，洗衣工厂系统；

洗衣洗鞋店软件功能介绍: 预约上门收衣智能提醒&#xff0b;员工手机抢单&#xff0b;地图导航&#xff0b;拍照同步上传 智能通知会员&#xff0c;消费通知&#xff0b;取衣通知&#xff0b;衣物到期提醒&#xff0b;消费提醒&#xff0b;取衣提醒 快速完成订单&#xff0c…
阅读更多...
esp32-S3 + visual studio code 开发环境搭建

esp32-S3 + visual studio code 开发环境搭建

一、首先在下面链接网页中下载esp-idf v5.1.1离线安装包 &#xff0c;并安装到指定位置。dl.espressif.cn/dl/esp-idf/https://dl.espressif.cn/dl/esp-idf/ 安装过程中会提示需要长路径支持&#xff0c;所以windows系统需要开启长路径使能 Step 1&#xff1a; 打开运行&…
阅读更多...
Jenkins部署失败：no space left on device

Jenkins部署失败：no space left on device

Jenkins部署到最后一步时报错&#xff1a;no space left on device&#xff0c;没有可用的空间使用了。 查看磁盘空间使用情况&#xff1a; df -h发现/home/data路径空间已经使用100%。 排查此路径下存在哪些大文件。 //查看系统中文件的使用情况 df -h -T //查看当前目录下各…
阅读更多...
众和策略可靠吗？中国资产，一夜狂飙！

众和策略可靠吗？中国资产，一夜狂飙！

可靠 当地时间10月24日&#xff0c;美股三大股指收高&#xff0c;其间道指涨0.62%&#xff0c;接连四个生意日下跌之后反弹&#xff0c;标普指数涨0.73%&#xff0c;纳斯达克指数涨0.93%。 10年期美国国债收益率小幅下滑。可口可乐等公司的财报表现弱小。美10月企业活动加速&…
阅读更多...
Dynamics 365 重写自带按钮

Dynamics 365 重写自带按钮

必备工具&#xff1a;Ribbon Workbench 步骤&#xff1a; 1、查看默认按钮使用的方法名称 右键按钮选择自定义命令(Customise Command)&#xff0c;然后查看command使用的命令 2、在前台chrome浏览器中搜索对应的命令&#xff0c;查看命令细节 3、基于命令细节新建command&am…
阅读更多...
c语言进制的转换16进制转换2进制

c语言进制的转换16进制转换2进制

c语言进制的转换16进制转换2进制 c语言的进制的转换 c语言进制的转换16进制转换2进制一、16进制的介绍二、八四二一法则三、16进制转换2进制 一、16进制的介绍 十六进制&#xff1a; 十六进制逢十六进一&#xff0c;所有的数组是0到9和A到F组成&#xff0c;其中A代表10&#x…
阅读更多...
当我们说“架构”的时候，我们在说什么？---解读《ISO/IEC/IEEE 42010》国际标准

当我们说“架构”的时候，我们在说什么？---解读《ISO/IEC/IEEE 42010》国际标准

当我们说“架构”的时候&#xff0c;你想到的是什么&#xff1f; 程序员听到“架构”的时候&#xff0c;想到的是SSH、SSM三层架构&#xff0c;或者是SOA架构&#xff0c;或者是微服务架构等。 人力资源专业人员听到架构的时候想到可能是企业组织架构。 几乎每个行业专业都会…
阅读更多...
[Unity]给场景中的3D字体TextMesh增加描边方案二

[Unity]给场景中的3D字体TextMesh增加描边方案二

如图所示仅支持图片内的/*数字 下面是资源
阅读更多...
8.（vue3.x+vite）组件间通信方式之window挂实例

8.（vue3.x+vite）组件间通信方式之window挂实例

前端技术社区总目录（订阅之前请先查看该博客） 效果预览 父组件代码 <template><div><div>{{message }}</div><Child
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023