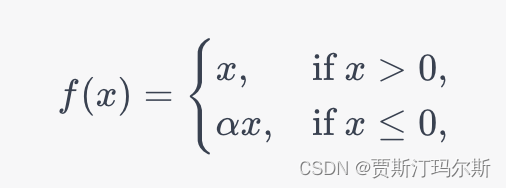1. Vector space

Vector space requirements v+w and c v are in the space, all combs c v + d w are in the space

但是“子空间”和“子集”的概念有区别，所有元素都在原空间之内就可称之为子集，但是要满足对线性运算封闭的子集才能成为子空间

中 2 subspaces

L: line is a subspace

P: Plane through [0,0,0]T is a subspace of 

 = all vectors in P or L or both is not a subspace

= all vectors in both P and L is a subspace - null space

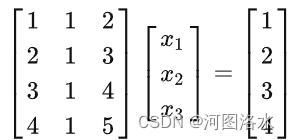
2. 列空间 Column space

column space of A is subspace of   is C(A)=all linear combs. of columns

Does Ax=b have a solution for every b? No

cuz 4 equations and 3 unknowns 列向量的线性组合无法充满

which b's allow this system to be solved?

Can solve Ax=b exactly when b is in C(A) IN 

由于列向量不是线性无关的，第三个列向量为前两个列向量之和，所以尽管有3个列向量，但是只有2个对张成向量空间有贡献。矩阵A的列空间为内的一个二维子空间

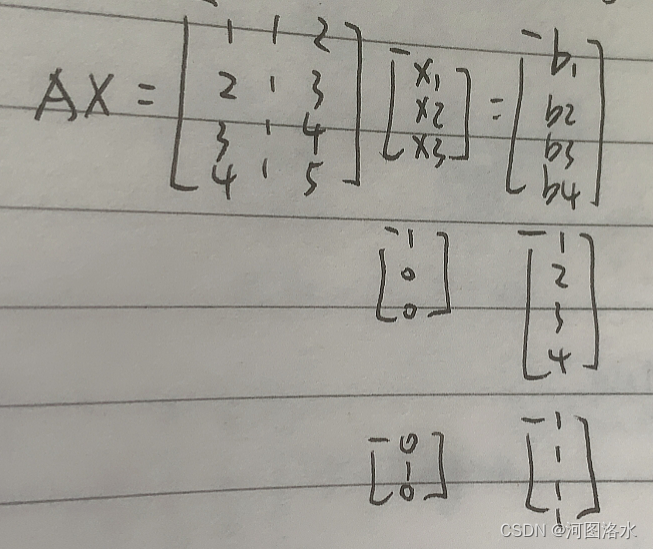
3.零空间（或化零空间）Nullspace

Null space of A = all solutions x =  in  to Ax=0

对于所给定这个矩阵A，其列向量含有4个分量，因此列空间是空间的子空间。

x为含有3个分量的向量，故矩阵A的零空间是的子空间。对于mxn矩阵，列空间为的子空间，零空间为空间的子空间。

N(A) contains  which is a line in 

check that - solution to Ax=0 always give a subspace

if Av=0 and Aw = 0 then A(v+w)=0

then A(12v)=0

4. influence of b

subspaces have to go through the origin

5. summary: 

2种构筑子空间方法

1.对于列空间，它是由列向量进行线性组合张成的空间

2.零空间是从方程组出发，通过让x满足特定条件而得到的子空间