【Matlab-基于形态学的权重自适应去噪】
- 1 引言
- 2 数学形态学原理
- 3 权重自适应的多结构形态学去噪
- 4 实现代码
- 4.1 主函数代码
- 4.2 串、并联去噪
- 4.3 图像权值计算
- 4.4 计算 PSNR 值
- 5 实验结果
参考书籍:计算机视觉与深度学习实战:以MATLAB、Python为工具,
主编:刘衍琦, 詹福宇, 王德建
北京:电子工业出版社,2019
1 引言
数字图像的噪声主要产生于获取、传输图像的过程中。常见的噪声主要有高斯噪声和椒盐噪声。其中,高斯噪声主要是由摄像机传感器元器件内部产生的;椒盐噪声主要是由图像切割所产生的黑白相间的亮暗点噪声,“椒”表示黑色噪声,“盐”表示白色噪声。图像去噪是指减少数字图像中噪声的过程,被广泛应用于图像处理领域的预处理过程。
数字图像去噪也可以分为空域图像去噪和频域图像去噪。空域图像去噪常用的有均值滤波算法和中值滤波算法,主要是对图像像素做邻域的运算来达到去噪效果。频域图像去噪首先是对数字图像进行某种变换,将其从空域转换到频域,然后对频域中的变换系数进行处理,最后对图像进行反变换,将其从频域转换到空域来达到去噪效果。其中,对图像进行空域和频域相互转换的方法有很多,常用的有傅里叶变换、小波变换等。
数学形态学以图像的形态特征为研究对象,通过设计一套独特的数字图像处理方法和理论来描述图像的基本特征和结构,通过引入集合的概念来描述图像中元素与元素、部分与部分的关系运算。因此,数学形态学的运算由基础的集合运算(并、交、补等)来定义,并且所有的图像矩阵都能被方便地转换为集合。随着集合理论研究的不断深入和实际应用的拓展,图像形态学处理也在图像分析、模式识别等领域起着重要的应用。
2 数学形态学原理
形态变换按应用场景可以分为二值变换和灰度变换两种形式。其中,二值变换一般用于处理集合,灰度变换一般用于处理函数。基本的形态变换包括腐蚀、膨胀、开运算和闭运算。 假设 f(x)和g(x)为被定义在二维离散空间F和G上的两个离散函数,其中f(x)为输入图像,g(x)为结构元素,则f(x)关于g(x)的腐蚀和膨胀分别被定义为:
( f Θ g ) ( x ) = min y ∈ G [ f ( x + y ) − g ( y ) ] ( 1 ) ( f ⊕ g ) ( x ) = max y ∈ G [ f ( x − y ) + g ( y ) ] ( 2 ) \begin{aligned} & (f \Theta g)(x)=\min _{y \in G}[f(x+y)-g(y)] \qquad(1) \\ & (f \oplus g)(x)=\max _{y \in G}[f(x-y)+g(y)] \qquad(2)\end{aligned} (fΘg)(x)=y∈Gmin[f(x+y)−g(y)](1)(f⊕g)(x)=y∈Gmax[f(x−y)+g(y)](2)
f(x)关于g(x)的开运算和闭运算分别被定义为:
( f ∘ g ) ( x ) = [ ( f Θ g ) ⊕ g ] ( x ) ( 3 ) ( f ∙ g ) ( x ) = [ ( f ⊕ g ) Θ g ] ( x ) ( 4 ) \begin{aligned} & (f \circ g)(x)=[(f \Theta g) \oplus g](x) \qquad(3) \\ & (f \bullet g)(x)=[(f \oplus g) \Theta g](x) \qquad(4)\end{aligned} (f∘g)(x)=[(fΘg)⊕g](x)(3)(f∙g)(x)=[(f⊕g)Θg](x)(4)
脉冲噪声是一种常见的图像噪声,根据噪声的位置灰度值与其邻域的灰度值的比较可以分为正、负脉冲。其中,正脉冲噪声的位置灰度值要大于其邻域的灰度值,负脉冲则相反。从公式(2)、公式(3)可以看出,开运算先腐蚀后膨胀,可用于过滤图像中的正脉冲噪声;闭运算先膨胀后腐蚀,可用于过滤图像中的负脉冲噪声。因此,为了同时消除图像中的正负脉冲噪声,可采用形态开-闭的级联形式,构成形态开闭级联滤波器。形态开-闭(OC) 和形态闭-开 (CO) 级联滤波器分别被定义为:
O C ( f ( x ) ) = ( f ∘ g ∙ g ) ( x ) ( 4 ) CO ( f ( x ) ) = ( f ∙ g ∘ g ) ( x ) ( 5 ) \begin{aligned} & \mathrm{OC}(f(x))=(f \circ g \bullet g)(x) \qquad(4) \\ & \operatorname{CO}(f(x))=(f \bullet g \circ g)(x)\qquad(5) \end{aligned} OC(f(x))=(f∘g∙g)(x)(4)CO(f(x))=(f∙g∘g)(x)(5)
根据集合运算与形态运算的特点,形态开-闭和形态闭-开级联滤波器具有平移不变性、递增性、对偶性和幂等性。
3 权重自适应的多结构形态学去噪
在数学形态学图像去噪的过程中,通过适当地选取结构元素的形状和维数可以提升滤波去噪的效果。在多结构元素的级联过程中,需要考虑到结构元素的形状和维数。假设结构元素集为Amn,n代表形状序列,m代表维数序列,则:
A n m = { A 11 , A 12 , ⋯ , A 1 m , A 21 , ⋯ , A n m } ( 6 ) \boldsymbol{A}_{n m}=\left\{A_{11}, A_{12}, \cdots, A_{1 m}, A_{21}, \cdots, A_{n m}\right\}\qquad(6) Anm={A11,A12,⋯,A1m,A21,⋯,Anm}(6)
A 11 ⊂ A 11 ⊂ ⋅ ⋅ ⋅ ⊂ A 1 m A 21 ⊂ A 21 ⊂ ⋅ ⋅ ⋅ ⊂ A 2 m ⋅ ⋅ ⋅ A n 1 ⊂ A n 1 ⊂ ⋅ ⋅ ⋅ ⊂ A n m ( 7 ) A_{11}\subset A_{11}\subset\cdot \cdot \cdot \subset A_{1m}\\A_{21}\subset A_{21}\subset\cdot \cdot \cdot \subset A_{2m} \\\cdot \cdot \cdot \\A_{n1}\subset A_{n1}\subset\cdot \cdot \cdot \subset A_{nm}\qquad(7) A11⊂A11⊂⋅⋅⋅⊂A1mA21⊂A21⊂⋅⋅⋅⊂A2m⋅⋅⋅An1⊂An1⊂⋅⋅⋅⊂Anm(7)
式中,A11包含于A12,因为A12继承了A11的信息并加入了腐蚀算子形成A12,依此类推.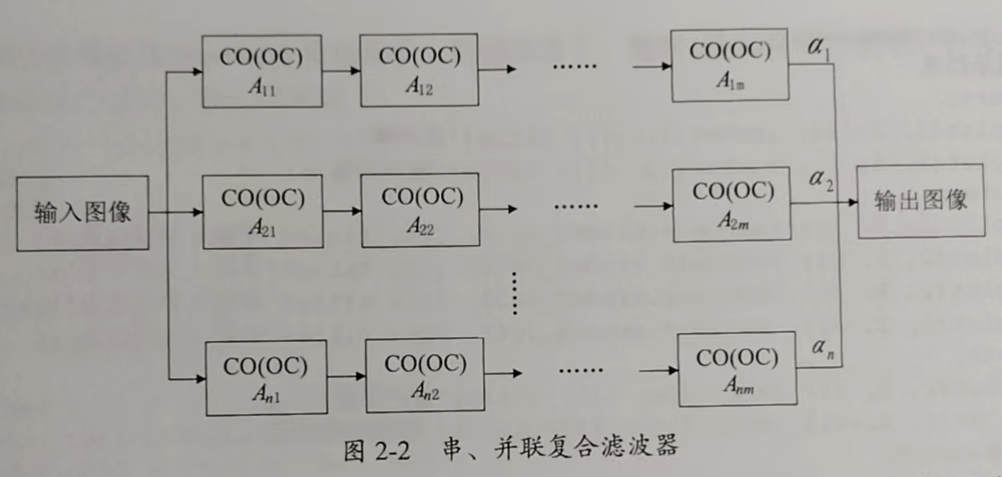
假设输入图像为f(x),经某种形状的结构元素的串形滤波结果为fi(x),i=1,2,…,n,则输出图像为 F(x)。其中,结构元素通过公式(8) 所示的自适应算法确定
α
1
,
α
2
,
⋅
⋅
⋅
,
α
i
\alpha_1,\alpha_2,\cdot \cdot \cdot ,\alpha_i
α1,α2,⋅⋅⋅,αi,则:
α i = β i β 1 + β 2 + ⋅ ⋅ ⋅ + β n ( 8 ) \alpha_i =\frac{\beta_i}{\beta_1+\beta_2+\cdot \cdot \cdot +\beta_n}\qquad(8) αi=β1+β2+⋅⋅⋅+βnβi(8)
F ( x ) = ∑ i = 1 n α i f i ( x ) ( 9 ) F(x)=\sum_{i=1}^{n} \alpha_i f_i (x)\qquad(9) F(x)=∑i=1nαifi(x)(9)
为了简化算法实验步骤,在具体实现过程中,可以选择将串联处理结果与原始图像进行差异值计算的方式来作为权值向量,再通过对串联结果加权求和的方式进行计算。因此,为了对数字图像进行数学形态学滤波器级联滤波去噪的仿真,本实验选择一幅人脸图像,加入泊松噪声,通过构建不同的串联滤波器、并联滤波器进行滤波去噪实验,最后通过计算并绘制PSNR 值曲线来显示去噪效果。
原图是一张人物灰度图:

文件结构如下:
.
└─ ErodeList.m
└─ GetRateList.m
└─ GetRemoveResult.m
└─ GetStrelList.m
└─ main.m
└─ PSNR.m
└─ images
└─im.jpg
4 实现代码
4.1 主函数代码
main.m
clc; clear all; close all;
filename = fullfile(pwd, 'images/im.jpg');
Img = imread(filename);
if ndims(Img) == 3
I = rgb2gray(Img);
else
I = Img;
end
Ig = imnoise(I,'poisson');
s = GetStrelList();
e = ErodeList(Ig, s);
f = GetRateList(Ig, e);
Igo = GetRemoveResult(f, e);
figure;
subplot(1, 2, 1); imshow(I, []); title('原图像');
subplot(1, 2, 2); imshow(Ig, []); title('噪声图像');
figure;
subplot(2, 2, 1); imshow(e.eroded_co12, []); title('串联1处理结果');
subplot(2, 2, 2); imshow(e.eroded_co22, []); title('串联2处理结果');
subplot(2, 2, 3); imshow(e.eroded_co32, []); title('串联3处理结果');
subplot(2, 2, 4); imshow(e.eroded_co42, []); title('串联4处理结果');
figure;
subplot(1, 2, 1); imshow(Ig, []); title('噪声图像');
subplot(1, 2, 2); imshow(Igo, []); title('并联去噪图像');
psnr1 = PSNR(I, e.eroded_co12);
psnr2 = PSNR(I, e.eroded_co22);
psnr3 = PSNR(I, e.eroded_co32);
psnr4 = PSNR(I, e.eroded_co42);
psnr5 = PSNR(I, Igo);
psnr_list = [psnr1 psnr2 psnr3 psnr4 psnr5];
figure;
plot(1:5, psnr_list, 'r+-');
axis([0 6 18 24]);
set(gca, 'XTick', 0:6, 'XTickLabel', {'', '串联1', '串联2', '串联3', ...
'串联4', '并联', ''});
grid on;
title('PSNR曲线比较');
4.2 串、并联去噪
GetStrelList.m指定线性算子,返回结构体s,s输入去噪算子ErodeList.m中,返回去噪结构体e
GetStrelList.m
function s = GetStrelList()
s.co11 = strel('line',5,-45);
s.co12 = strel('line',7,-45);
s.co21 = strel('line',5,45);
s.co22 = strel('line',7,45);
s.co31 = strel('line',3,90);
s.co32 = strel('line',5,90);
s.co41 = strel('line',3,0);
s.co42 = strel('line',5,0);
ErodeList.m
function e = ErodeList(Ig, s)
e.eroded_co11 = imerode(Ig,s.co11);
e.eroded_co12 = imerode(e.eroded_co11,s.co12);
e.eroded_co21 = imerode(Ig,s.co21);
e.eroded_co22 = imerode(e.eroded_co21,s.co22);
e.eroded_co31 = imerode(Ig,s.co31);
e.eroded_co32 = imerode(e.eroded_co31,s.co32);
e.eroded_co41 = imerode(Ig,s.co41);
e.eroded_co42 = imerode(e.eroded_co41,s.co42);
4.3 图像权值计算
图像权值计算函数 GetRateList.m 将根据串联结果与原始图像的差异程度进行计算,图像并联去噪函数 GetRcmoveResult.m 将根据输入的权值向量、串联结果,通过加权求和的方式进行处理核心代码如下:
GetRateList.m
function f = GetRateList(Ig, e)
f.df1 = sum(sum(abs(double(e.eroded_co12)-double(Ig))));
f.df2 = sum(sum(abs(double(e.eroded_co22)-double(Ig))));
f.df3 = sum(sum(abs(double(e.eroded_co32)-double(Ig))));
f.df4 = sum(sum(abs(double(e.eroded_co42)-double(Ig))));
f.df = sum([f.df1 f.df2 f.df3 f.df4]);
GetRcmoveResult.m ,这里的权重计算方法是求差值,再求和,再除去中总的差值,即表示每部分差值占总差值的比例。
function Igo = GetRemoveResult(f, e)
Igo = f.df1/f.df*double(e.eroded_co12)+f.df2/f.df*double(e.eroded_co22)+...
f.df3/f.df*double(e.eroded_co32)+f.df4/f.df*double(e.eroded_co42);
Igo = mat2gray(Igo);
4.4 计算 PSNR 值
PSNR全称为“Peak Signal-to-Noise Ratio”,中文意思即为峰值信噪比,是衡量图像质量的指标之一。PSNR参考链接
PSNR值越大,表示图像的质量越好,一般来说:
(1)高于40dB:说明图像质量极好(即非常接近原始图像)
(2)30—40dB:通常表示图像质量是好的(即失真可以察觉但可以接受)
(3)20—30dB:说明图像质量差
(4)低于20dB:图像质量不可接受
为了对处理结果进行比较,这里采用计算 PSNR 值的方式将串联、并联处理结果与原始图像进行计算,并绘制 PSNR 值曲线进行分析。核心代码如下:
function S = PSNR(s,t)
[m, n, ~]=size(s);
s = im2uint8(mat2gray(s));
t = im2uint8(mat2gray(t));
s = double(s);
t = double(t);
sd = 0;
mi = m*n*max(max(s.^2));
for u = 1:m
for v = 1:n
sd = sd+(s(u,v)-t(u,v))^2;
end
end
if sd == 0
sd = 1;
end
S = mi/sd;
S = 10*log10(S);
5 实验结果
图1 原图和噪声图像

图2 串联去噪图像

图3 并联去噪图像

原图

图4 PSNR值曲线
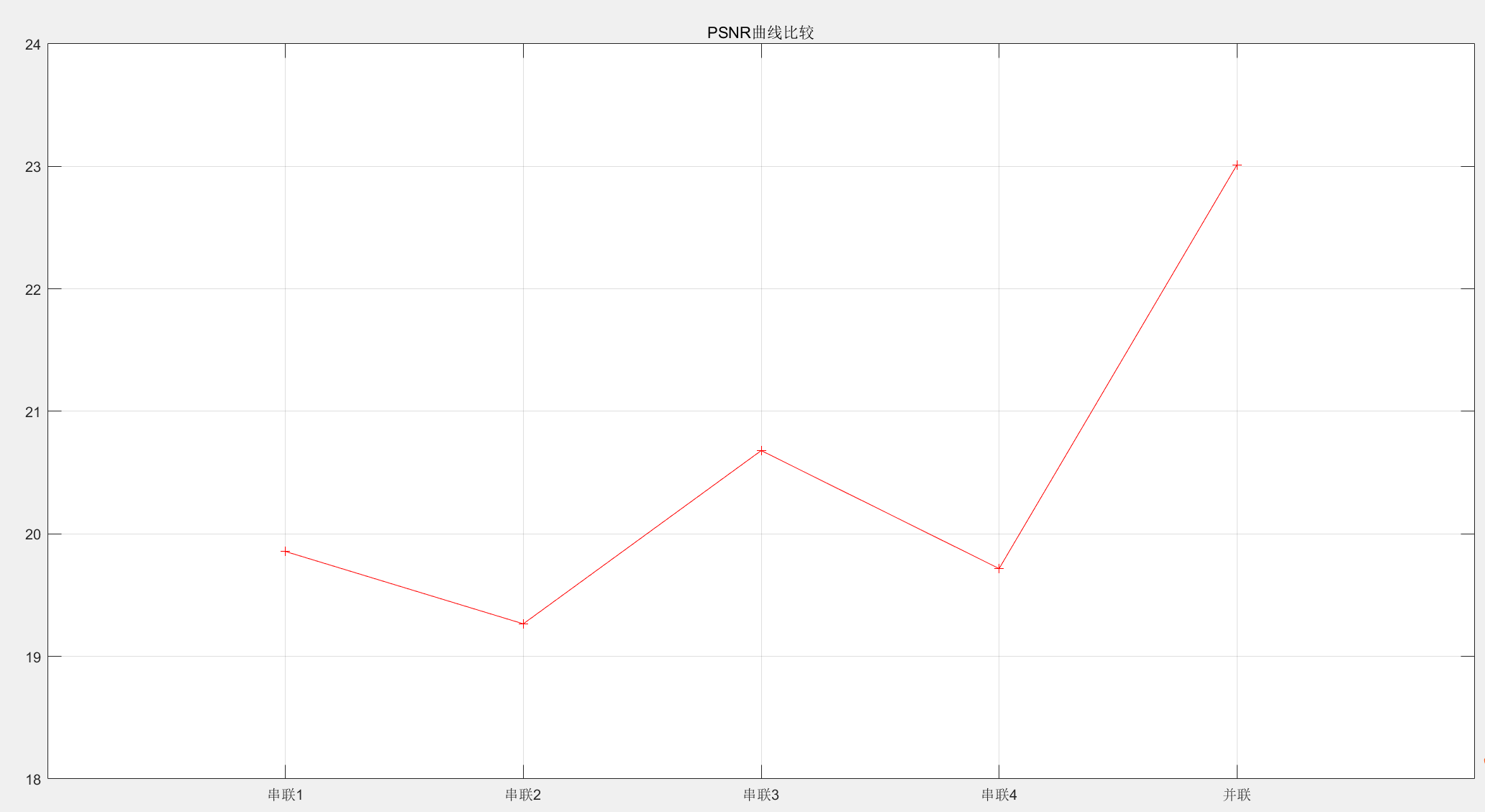
结论:实验结果表明,如果仅通过串联滤波器去噪,则往往具有一定的局限性,在结果图像中也保留着较为明显的噪声。通过并联滤波器进行滤波去噪得到的结果中 PSNR 值更高,而且结图像在视觉效果上要比只进行串联滤波器去噪更为理想。
将形态学滤波器通过串、并联来构建级联滤波器的方式应用于不同的图像处理过程中,在一定程度上能够影响普通滤波的效果,这也是一个研究方向。