摘要

近年来，多跳推理在获取更可解释的链接预测方面得到了广泛研究。然而，实验中发现，这些模型给出的许多路径实际上是不合理的，而对它们的可解释性评估工作却很少。本文提出了一个统一的框架，以定量评估多跳推理模型的可解释性，以推进它们的发展。

具体而言，定义了三个评估指标：

1. 路径回溯
2. 局部可解释性
3. 全局可解释性

并设计了一种使用规则的可解释性得分来计算这些指标的近似策略。

此外，手动注释了所有可能的规则，并建立了一个用于检测多跳推理可解释性的基准测试（BIMR）。

在实验中，验证了基准测试的有效性。此外，在基准测试上运行了九个代表性的基线模型，实验结果表明，当前多跳推理模型的可解释性不太令人满意，比基准测试给出的上限低了51.7%。此外，基于规则的模型在性能和可解释性方面优于多跳推理模型，这指向了未来研究的一个方向，即如何更好地将规则信息纳入多跳推理模型中。

1 引言

近年来，知识图谱（KG）的多跳推理得到了广泛研究。它不仅推断出新的知识，还提供了能够解释预测结果并使模型可信的推理路径。例如，图1展示了两个推理得出的三元组及其推理路径。

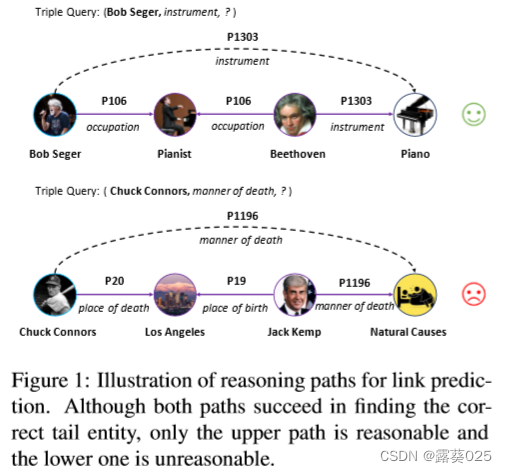
传统的KG嵌入模型（例如TransE）在给定查询（Bob Seger，instrument，?）的情况下隐式地找到目标实体piano，而多跳推理模型则完整地补充了三元组，并显式地输出推理路径（紫色实线箭头）。因此，多跳推理在实际系统中被期望更可靠，因为可以通过判断路径是否合理来安全地将推理得出的三元组添加到KG中。

大多数现有的多跳推理模型假设输出路径是合理的，并且更关注链接预测的性能。例如，MultiHop使用强化学习训练一个代理程序在知识图谱上进行搜索。代理程序找到的路径被认为是对预测结果的合理解释。然而，在手动标记后，超过60%的路径是不合理的。如图1的下部所示，给定一个三元组查询（Chuck Connors，manner of death，?），多跳推理模型通过推理路径（紫色实线箭头）找到了正确的尾部实体Natural Causes。虽然模型正确地完成了缺失的三元组，但这个推理路径是可疑的，因为死亡方式与一个人的出生或死亡城市无关。失败的可解释性主要是因为许多人出生和死亡地点相同，自然原因是主要的死亡方式。因此，这条路径只是统计上与查询三元组相关，并未提供可解释性。在实验中，这种不合理的路径在多跳推理模型中普遍存在，这表明迫切需要进行可解释性评估。

本文提出了一个统一的框架，用于自动评估多跳推理模型的可解释性。与以往主要依赖案例研究展示模型可解释性的工作不同，本文旨在通过计算模型生成的所有路径的可解释性得分进行定量评估。具体而言，定义了三个评估指标：路径回溯、局部可解释性和全局可解释性（详见第4.2节）。然而，给每个路径分配可解释性得分是非常耗时的，因为多跳推理可以生成的路径数量非常大。为了解决这个问题，提出了一种近似策略，通过忽略只剩下关系的实体将推理路径抽象为有限的规则（详见方程6和7）。以这种方式获得的规则总数要比路径数量小得多，并且将规则的可解释性得分分配给其对应的路径。探索了两种方法来为每个规则分配可解释性得分，即手动注释和通过规则挖掘方法自动生成。前者是本文的重点。具体而言，邀请注释员手动为所有可能的规则注释可解释性得分，以建立一个手动注释的基准测试（A-benchmark）。这个标注过程也面临一个挑战，即可解释性高度主观且难以注释。不同的注释员可能给出不同的解释。为了减少变异，为注释员提供了一些可解释的选项，而不是要求他们给出直接的分数。此外，对于每个样本，请十个注释员进行注释，并将他们的平均分数作为最终结果。除了A-benchmark，我们还提供了基于规则挖掘方法的基准测试（R-benchmark）。这些基准测试使用挖掘规则的置信度作为规则的可解释性得分。这种方法不如手动注释准确，但可以自动推广到大多数知识图谱。

在实验中验证了基准测试BIMR的有效性。
具体而言，使用抽样注释方法获得每个模型的可解释性，并将其与A-benchmark生成的结果进行比较。实验结果表明，它们之间的差距很小，这表明近似策略对结果的影响很小。此外，在基准测试上运行了九个代表性的基线模型。实验结果显示，现有的多跳推理模型的可解释性仍然不够令人满意，并且与A-benchmark给出的上界相差甚远。具体而言，即使是最好的多跳推理模型的可解释性也比上界低51.7%。在多跳推理的研究中，不仅应关注性能，还应关注可解释性。此外，基于规则的推理方法AnyBURL在性能和可解释性方面明显优于现有的多跳推理模型，这指向了一个可能的未来研究方向，即如何更好地将规则融入到多跳推理中。

2 相关工作

2.1 多跳推理

多跳推理模型在进行三元组补全时可以提供可解释的路径。现有的大多数多跳推理模型都是基于强化学习（RL）框架的。其中，DeepPath是第一个正式提出和解决使用RL进行多跳推理任务的工作，这激发了后来的许多工作，如DIVA和AttnPath。MINERVA是一个端到端模型，在解决多跳推理任务方面具有广泛的影响。在该模型的基础上，M-Walk和MultiHop分别通过离策略学习和奖励塑造来解决奖励稀疏性的问题。此外，还有一些其他模型，如DIVINE、R2D2、RLH和RuleGuider模型，它们分别从模仿学习、辩论动态、分层RL和规则引导四个方向改进多跳推理。CPL和DacKGR通过向知识图谱添加额外的三元组来增强模型的效果。

2.2 基于规则的推理

基于规则的推理与多跳推理类似，也可以执行可解释的三元组补全，只是它们给出相应的规则而不是具体的路径。基于规则的推理可以分为两类，即基于神经网络的模型和规则挖掘模型。其中，基于神经网络的模型在执行三元组补全时给出相应的规则，而规则挖掘模型首先挖掘规则，然后将其用于补全。

2.3 可解释性评估

尽管人们承认可解释性的重要性，但很少有研究工作针对可解释性评估进行研究。大多数多跳推理模型依赖案例研究来展示可解释性质量，而RuleGuider则通过采样测试并计算差异进行评估。在其他领域也有一些工作用于测试可解释性，但它们不能直接应用于知识图谱的多跳推理任务。

3 基础知识

知识图谱（KG） 被定义为一个有向图KG = {E,R,T}，其中E是实体的集合，R是关系的集合，T = {(h,r,t)} ⊆ E×R×E是三元组的集合。

多跳推理 旨在通过可解释的链接预测完成知识图谱。具体而言，对于给定的三元组查询（h,r,?），它需要预测正确的尾部实体t，并给出一个路径（h,r,t）←（h,r₁,e₁）∧（e₁,r₂,e₂）∧···∧（e_n−1,r_n,t）作为解释。

基于规则的推理 可以被视为广义的多跳推理，并且也可以在基准测试中进行评估。对于给定的三元组查询（h,r,?），它需要预测尾部实体t，并给出一些带有置信度的Horn规则作为解释，其中规则f的形式如下：

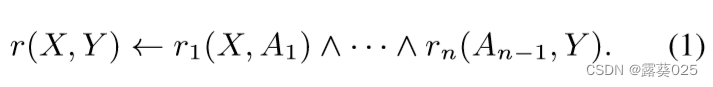
其中，大写字母表示变量，r(…)是规则的头部，r₁(…)∧···∧r_n(…)是规则的体部，r(h,r)等价于三元组（h,r,t）。为了得到与多跳推理任务相同的路径，按照置信度的降序对这些规则进行排序，并在知识图谱上进行匹配。

4 基准测试

为了定量评估多跳推理模型的可解释性，首先基于Wikidata（第4.1节）构建了一个数据集。在此之后，我们提出了一个通用的评估框架（第4.2节）。基于这个框架，我们应用了一种近似策略（第4.3节），并构建了具有人工注释的基准测试（第4.4节）和挖掘规则的基准测试（第4.5节）。

4.1 数据集构建

基于Wikidata以及广泛使用的FB15K-237构建了一个可解释的数据集WD15K。

旨在利用Wikidata中易于阅读的关系，同时保持来自FB15K-237的实体不变。依赖于Wikidata中每个实体的Freebase ID属性来连接这两个数据源，数据集WD15K的统计信息如表1所示。对其进行了洗牌，并将90％/5％/5％作为训练/验证/测试集。由于篇幅限制，将数据集构建的详细步骤放在补充材料中（附录A）。

4.2 评估框架

本文提出了一个通用框架来定量评估多跳推理模型的可解释性。具体而言，测试集中的每个三元组（h,r,t）被转换为一个三元组查询（h,r,?）。模型需要预测t和可能的推理路径。因此，计算了模型的可解释性分数，该分数基于三个指标进行定义：

1. 路径召回率（PR）
2. 局部可解释性（LI）
3. 全局可解释性（GI）。

路径召回率（PR） 表示在测试集中能够至少找到一条从头实体到尾实体的路径的三元组的比例。它的形式定义如下：

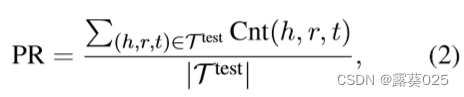
其中Cnt(h,r,t)是一个指示函数，用于表示模型是否能够从h找到一条到t的路径。如果至少有一条路径被找到，则函数值为1，否则为0。路径召回率（PR）是必要的，因为对于大多数模型而言，并非每个三元组都能够找到从头实体到尾实体的路径。对于基于RL的多跳推理模型（例如MINERVA），束搜索大小是一个关键的超参数，直接影响PR。束搜索大小越大，模型能够找到的路径就越多。但在实际情况下，束搜索大小不能无限大。也就是说，对于每个三元组查询（h,r,?），路径的数量存在一个上限。另一方面，可能不存在从h到t的路径，或者我们可能无法在知识图谱上匹配每个规则的真实路径。这导致Cnt(h,r,t) = 0。

局部可解释性（LI） 用于评估模型找到的路径的合理性。它的定义如下：

其中p是模型找到的从h到t的最佳路径（具有最高分数的路径），而S§是该路径的可解释性分数，将在下一节介绍。

全局可解释性（GI） 评估模型的整体可解释性，因为局部可解释性只能表达模型找到的路径的合理程度，而没有考虑可以找到多少条路径。
定义GI如下：

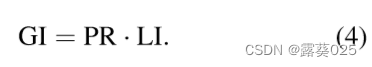
对LI和GI进行总结和比较。具体而言，LI可以反映可以找到的所有路径的可解释性，而GI评估模型的整体可解释性。

4.3 近似可解释性评分

基于WD15K和上述评估框架，可以构建基准测试来定量评估可解释性。然而，由于路径数量巨大，评估框架中的S§很难获得。因此，在具体构建之前，需要进行一些准备工作，即路径收集和近似策略。

路径收集 这一步旨在收集从h到t的所有可能路径，以便评估框架可以覆盖多跳推理模型的各种输出。
具体而言，首先为训练集中的每个三元组（h,r,t）添加逆转的三元组（t,r⁻¹,h）。然后，对于WD15K中的每个测试三元组（h,r,t），使用广度优先搜索（BFS）在训练集上搜索从h到t的所有路径，路径长度不超过3，即路径中最多有三个关系。这在多跳推理模型（例如MultiHop）中被广泛使用，因为过多的跳数会大大增加搜索空间并降低可解释性。经过去重处理，得到了最终的路径集合P，包含约1600万条路径，涵盖了多跳推理模型可能发现的所有路径。

近似优化 提出了一种近似策略，以避免对路径集合P（即1600万条路径）进行不切实际的注释或计算。基于观察，发现路径的可解释性主要来自规则而不是特定实体。因此，将路径p ∈ P抽象为相应的规则f，并使用规则的可解释性分数S(f)作为路径的可解释性分数S§，即：

在进行这种转换后，将P转换为一组规则F。由于规则是与实体无关的，F的大小大大减小为96,019个，只需要给每个规则f ∈ F一个可解释性分数S(f)来构建基准测试。

接下来，将介绍两种获取规则可解释性分数的方法。

4.4 Benchmark with Manual Annotation

对F中的每个规则进行手动标注，为其分配一个可解释性分数，以形成一个手动注释的基准测试（A-benchmark）。该基准测试的具体构建过程可以分为两个步骤，即修剪优化和手动标注。
下面将分别详细介绍这两部分。

修剪优化 提出了一种修剪策略，以节省注释成本，同时对最终结果产生较小的影响。规则挖掘方法可以在知识图谱上自动挖掘规则，并为每个获得的规则给予置信度分数。修剪策略基于以下假设：

那些不在规则挖掘方法挖掘出的规则列表中的规则，或者那些置信度非常低的规则，其可解释性分数要低得多。

下面展示了确认性实验来验证假设。

在具体的实现中，使用AnyBURL在训练集上挖掘规则，并得到36,065个规则FA，其中AnyBURL是最好的规则挖掘方法之一，在许多数据集上实现了SOTA性能。基于FA中的规则及其置信度分数，将整个规则集合F分为三组，即高置信度规则（H规则）、低置信度规则（L规则）和其他规则（O规则）。从每组中随机抽取500个规则，并邀请专家们根据可解释性分数对其进行手动标注。规则的分类标准和标注结果如表2所示。

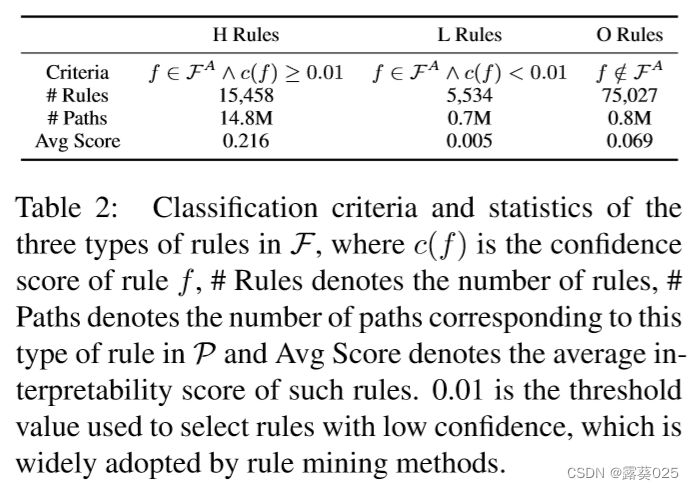
根据表2可以发现L规则的平均可解释性分数要远低于H规则。虽然O规则的平均分数不及L规则那么小，但它们对应的路径数量较少（0.8百万），而规则数量相对较大（75,027）。因此，O规则可以被视为“长尾”规则。

为了节省标注成本，并尽可能不影响最终的评估结果，只对H规则手动标注可解释性分数。对于其余的规则，使用该类型规则的平均分数作为它们的可解释性分数。具体而言，参考表2的结果，统一将L规则的可解释性分数设定为0.005，O规则的可解释性分数设定为0.069。

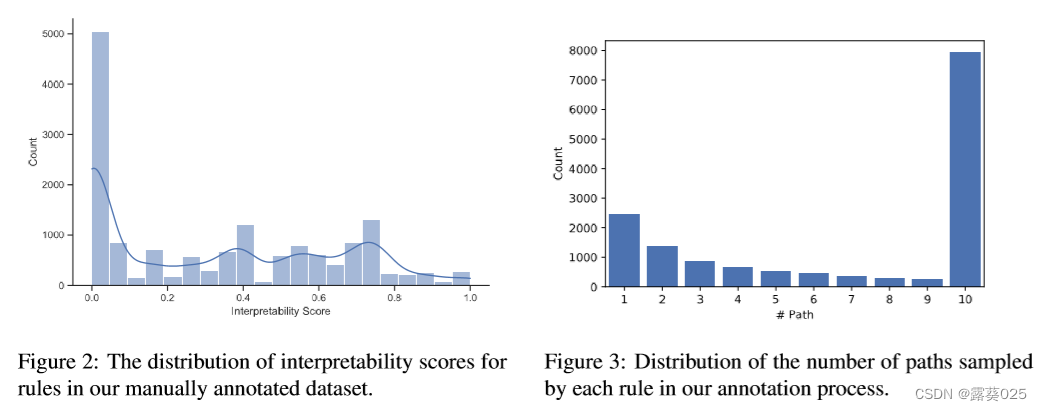
手动标注 由于对于标注者来说直接标注规则的可解释性分数是困难的，对于F中的每个H规则，从P中随机抽取最多十个对应的真实路径进行标注。这里存在一个评估效果和标注成本之间的权衡。如果某些规则在P中的真实路径少于十个，将对所有路径进行标注。标注后，使用与规则对应的路径的平均可解释性分数作为该规则的分数。具体而言，对于规则f，其可解释性分数定义为：

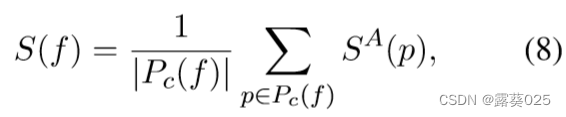
其中P_c(f)是规则f的所有抽样路径，S^A§是路径p的可解释性分数，通过手动标注获得。值得注意的是，无法对P中的所有路径进行标注。对于方程8中标注的少数路径，可以直接获得它们的S§ = S^A§，而对于大多数其他路径，使用方程5来获得它们的近似可解释性分数。

对于F中的15,458个H规则，最终得到了102,694个相关的真实路径。平均每个规则对应6.65个真实路径。直接为每个路径给出可解释性分数是一项主观且困难的任务。为了消除主观性的影响并简化标注过程，对于每个真实路径，让标注者选择以下三个选项之一：合理（reasonable）、部分合理（partially reasonable）和不合理（unreasonable）。这三个选项分别对应可解释性分数的1、0.5和0分。也尝试将选项数设置为2（合理和不合理）或4（合理、最合理、少数合理和不合理），但最终标注的准确性会降低。因此，最终采用了当前的三级可解释性分数划分。

为了进一步降低标注的难度，使用Graphviz工具将抽象路径转换为图片。附录C中给出了一个标注示例。

表3展示了我们标注数据集中的一些案例，其中规则的可解释性分数是它所抽样路径分数的平均值。

4.5 使用挖掘规则的基准

除了A基准之外，还构建了使用挖掘规则的基准（R基准）。具体而言，使用规则挖掘方法在训练集上挖掘规则。这些挖掘到的规则形成了规则集合F*（对于AnyBURL，F*等于FA）。可以使用规则的置信度作为可解释性分数。但是这会引入另一个问题，即规则的置信度和可解释性分数之间缺乏校准。

为了解决这个问题，类似于第4.4节中的手动标注，需要使用三个分类（合理、部分合理和不合理）来标注一些规则的可解释性分数。定义两个阈值h1和h2，规则f的分类类型Type(f)定义如下：

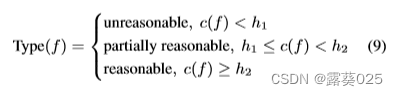
其中c(f)是规则f的置信度得分。可以将其视为一个三分类任务，其中预测的类型是Type(f)，而黄金类型是标注结果。使用Micro-F1分数来寻找最佳的h1和h2，即搜索可以获得最高Micro-F1分数的最佳h1和h2。

最后，对于每个规则f ∈ F，如果f /∈ F*，则S(f) = 0。否则，可以根据方程9得到Type(f)，然后获得可解释性分数S(f)。具体而言，不合理、部分合理和合理对应于0、0.5和1。

讨论 上述两种基准方法针对准确性和泛化性在不同情况下进行了目标设定。一方面，手动标注提供可靠的评估结果，但成本高且仅限于特定数据集（例如WD15K）。另一方面，自动规则挖掘方法可以应用于任意的知识图谱补全数据集，但可能会导致不准确的可解释性分数，因为规则的置信度和可解释性分数之间没有绝对的相关性。在获得上述基准之后，对其进行了统计分析。例如，给出了可解释性分数的分布以及可解释性分数最高和最低的20个关系。此外，还分析了可解释性分数和置信度分数之间的关系。由于篇幅限制，将这些内容放在附录B中。

实验