文章目录
- 统计学习方法 支持向量机(上)
- 线性可分支持向量机与硬间隔最大化
- 定义
- 硬间隔最大化
- 对偶算法
- 线性支持向量机与软间隔最大化
- 定义
- 软间隔最大化
- 对偶算法
- 合页损失函数
统计学习方法 支持向量机(上)
读李航的《统计学习方法》中,关于支持向量机的相关笔记。
支持向量机(SVM)是一种二分类模型。其学习策略为间隔最大化,可形式化为一个求解凸二次规划的问题,同时也等价于正则化荷叶损失函数最小化的问题。间隔最大使它有别于感知机。
线性可分支持向量机与硬间隔最大化
线性可分支持向量机使用硬间隔最大化的算法,因此要求线性可分的训练数据集。
定义
线性可分支持向量机:给定线性可分数据集,通过硬间隔最大化或等价求解相应的凸二次规划问题学习到的分离超平面:
w
∗
⋅
x
+
b
∗
=
0
w^\ast \cdot x+b^\ast=0
w∗⋅x+b∗=0
以及相应的分类决策函数:
f
(
x
)
=
sign
(
w
∗
⋅
x
+
b
∗
)
f(x)=\text{sign}(w^\ast \cdot x+b^\ast)
f(x)=sign(w∗⋅x+b∗)
称为线性可分支持向量机。
函数间隔:给定训练数据
T
T
T 与超平面
(
w
,
b
)
(w,\,b)
(w,b),超平面关于样本点
(
x
1
,
y
i
)
(x_1,\,y_i)
(x1,yi) 的函数间隔为:
γ
^
i
=
y
i
(
w
⋅
x
i
+
b
)
\hat{\gamma}_i=y_i(w \cdot x_i+b)
γ^i=yi(w⋅xi+b)
- 超平面参数确定的情况下,函数间隔可以反映样本点距离超平面的远近和分类的正确性与可信度;
几何间隔:给定训练数据
T
T
T 与超平面
(
w
,
b
)
(w,\,b)
(w,b),超平面关于样本点
(
x
1
,
y
i
)
(x_1,\,y_i)
(x1,yi) 的几何间隔为:
γ
^
i
=
1
∣
∣
w
∣
∣
y
i
(
w
⋅
x
i
+
b
)
\hat{\gamma}_i=\frac{1}{||w||}y_i(w \cdot x_i+b)
γ^i=∣∣w∣∣1yi(w⋅xi+b)
- 几何间隔表示样本点到超平面的距离带上是否分类正确的符号,即带符号的距离;
- 函数间隔的大小受到 w w w 和 b b b 的 scale 的影响,但几何间隔反映了实际距离,二者的关系为:
γ = γ ^ ∣ ∣ w ∣ ∣ \gamma=\frac{\hat{\gamma}}{||w||} γ=∣∣w∣∣γ^
其中:
γ
=
min
i
=
1
,
⋯
,
N
γ
i
,
γ
^
=
min
i
=
1
,
⋯
,
N
γ
^
i
\gamma=\min\limits_{i=1,\cdots,N}\gamma_i ,\quad\quad \hat\gamma=\min\limits_{i=1,\cdots,N}\hat\gamma_i
γ=i=1,⋯,Nminγi,γ^=i=1,⋯,Nminγ^i
硬间隔最大化
硬间隔最大化:SVM 学习的基本想法是,求解能够正确划分数据集、并且几何间隔最大的分离超平面。对于线性可分的数据集,可正确划分的超平面可能有无穷多个,但几何间隔最大的分离超平面是唯一的。
也就是说,我们要找到的分离超平面,不仅可以正确划分数据,同时还能与数据保持尽量远的距离,这样灵活性更高,加入新的未知的实例时能有更好的分类预测能力。
该问题可以表示为下面的约束最优化问题:
max
w
,
b
γ
s.t.
1
∣
∣
w
∣
∣
y
i
(
w
⋅
x
i
+
b
)
≥
γ
,
i
=
1
,
2
,
⋯
,
N
\begin{array}{l} \max\limits_{w,\,b} \gamma \\ \text{s.t. } \frac{1}{||w||}y_i(w \cdot x_i+b) \geq \gamma,\quad i=1,2,\cdots,N \end{array}
w,bmaxγs.t. ∣∣w∣∣1yi(w⋅xi+b)≥γ,i=1,2,⋯,N
使用函数间隔的话,可以表示为:
max
w
,
b
γ
^
∣
∣
w
∣
∣
s.t.
y
i
(
w
⋅
x
i
+
b
)
≥
γ
^
,
i
=
1
,
2
,
⋯
,
N
\begin{array}{l} \max\limits_{w,\,b} \frac{\hat{\gamma}}{||w||} \\ \text{s.t. } y_i(w \cdot x_i+b) \geq \hat\gamma,\quad i=1,2,\cdots,N \end{array}
w,bmax∣∣w∣∣γ^s.t. yi(w⋅xi+b)≥γ^,i=1,2,⋯,N
函数间隔的取值并不影响最优化问题的解,因为比如将
w
w
w 和
b
b
b 等比例放大为
λ
w
\lambda w
λw 和
λ
b
\lambda b
λb ,此时函数间隔也变为
λ
γ
^
\lambda\hat\gamma
λγ^ 。所以可以取
γ
^
=
1
\hat\gamma=1
γ^=1 ,这样问题转化为:
min
w
,
b
1
2
∣
∣
w
∣
∣
2
s.t.
y
i
(
w
⋅
x
i
+
b
)
−
1
≥
0
,
i
=
1
,
2
,
⋯
,
N
\begin{array}{l} \min\limits_{w,\,b} \frac{1}{2}||w||^2 \\ \text{s.t. } y_i(w \cdot x_i+b) -1 \geq 0,\quad i=1,2,\cdots,N \end{array}
w,bmin21∣∣w∣∣2s.t. yi(w⋅xi+b)−1≥0,i=1,2,⋯,N
这样就变成了一个凸二次规划的问题。
凸二次规划问题:约束最优化问题,形如:
min
w
f
(
w
)
s.t.
g
i
(
w
)
≤
0
,
i
=
1
,
2
,
⋯
,
k
h
i
(
w
)
=
0
,
i
=
1
,
2
,
⋯
,
l
\begin{aligned} \min\limits_w &\, f(w) \\ \text{s.t. } &\, g_i(w)\leq 0,\quad i=1,2,\cdots,k \\ &\, h_i(w)= 0,\quad i=1,2,\cdots,l \\ \end{aligned}
wmins.t. f(w)gi(w)≤0,i=1,2,⋯,khi(w)=0,i=1,2,⋯,l
目标函数
f
(
w
)
f(w)
f(w) 和约束函数
g
i
(
w
)
g_i(w)
gi(w) 都是
R
n
\R^n
Rn 上连续可微的凸函数(convex function),而约束函数
h
i
(
w
)
h_i(w)
hi(w) 是
R
n
\R^n
Rn 上的仿射函数(即线性变换函数,
f
(
x
)
=
a
⋅
x
+
b
f(x)=a\cdot x+b
f(x)=a⋅x+b);
算法:线性可分支持向量机学习算法 - 最大间隔法
- 输入:线性可分训练数据集 T = { ( x 1 , t 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } T=\set{(x_1,t_1),(x_2,y_2),\cdots,(x_N,y_N)} T={(x1,t1),(x2,y2),⋯,(xN,yN)} ,其中 x i ∈ X ⊆ R n x_i\in\mathcal{X}\subseteq \R^n xi∈X⊆Rn , y i ∈ Y = { 1 , − 1 } y_i\in\mathcal{Y}=\set{1,\,-1} yi∈Y={1,−1}
- 输出:最大间隔分离超平面和分类决策函数
- 构造并求解约束最优化问题:
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 s.t. y i ( w ⋅ x i + b ) − 1 ≥ 0 , i = 1 , 2 , ⋯ , N \begin{array}{l} \min\limits_{w,\,b} \frac{1}{2}||w||^2 \\ \text{s.t. } y_i(w \cdot x_i+b) -1 \geq 0,\quad i=1,2,\cdots,N \end{array} w,bmin21∣∣w∣∣2s.t. yi(w⋅xi+b)−1≥0,i=1,2,⋯,N
求得最优解 w ∗ w^\ast w∗ , b ∗ b^\ast b∗ ;
- 由此得到分离超平面:
w ∗ ⋅ x + b ∗ = 0 w^\ast \cdot x+b^\ast = 0 w∗⋅x+b∗=0
分类决策函数:
f
(
x
)
=
sign
(
w
∗
⋅
x
+
b
∗
)
f(x)=\text{sign}(w^\ast \cdot x+b^\ast)
f(x)=sign(w∗⋅x+b∗)
最大间隔分离超平面的存在唯一性:如果训练数据 T T T 线性可分,则可以将所有样本点正确分开并且最大间隔的分离超平面存在且唯一。
(存在性很明显,唯一性由凸最优问题的解的唯一性可以得到)
支持向量:所谓的支持向量,就是处在离超平面最近的间隔上的点,即:
y
i
(
w
⋅
x
i
+
b
)
−
1
=
0
y_i(w \cdot x_i+b) -1 = 0
yi(w⋅xi+b)−1=0
y
i
=
+
1
y_i=+1
yi=+1 的支持向量在超平面:
H
1
:
w
⋅
x
+
b
=
1
H_1:\, w\cdot x+b=1
H1:w⋅x+b=1
y
i
=
−
1
y_i=-1
yi=−1 的支持向量在超平面:
H
2
:
w
⋅
x
+
b
=
−
1
H_2:\, w\cdot x+b=-1
H2:w⋅x+b=−1
间隔:
H
1
H_1
H1 和
H
2
H_2
H2 之间的距离称为间隔,为
2
∣
∣
w
∣
∣
\frac{2}{||w||}
∣∣w∣∣2 ;
H
1
H_1
H1 和
H
2
H_2
H2 称为间隔边界。
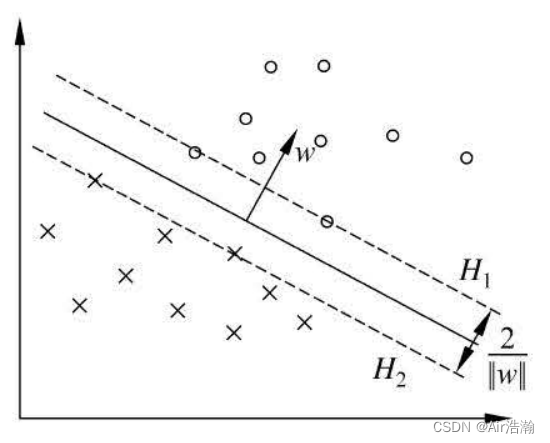
所以说 SVM 具有稀疏性,因为只有少数几个样本点(支持向量)在起作用。
对偶算法
对偶算法的推导:硬间隔最大化问题的 Lagrangian 为:
L
(
w
,
b
,
α
)
=
1
2
∣
∣
w
∣
∣
2
+
∑
i
=
1
N
α
i
(
1
−
y
i
(
w
⋅
x
i
+
b
)
)
=
1
2
∣
∣
w
∣
∣
2
−
∑
i
=
1
N
α
i
y
i
(
w
⋅
x
i
+
b
)
)
+
∑
i
=
1
N
α
i
\begin{aligned} L(w,b,\alpha)=&\, \frac{1}{2}||w||^2+ \sum\limits_{i=1}^N \alpha_i(1-y_i(w\cdot x_i+b)) \\ =&\, \frac{1}{2}||w||^2-\sum\limits_{i=1}^N \alpha_iy_i(w\cdot x_i+b))+\sum\limits_{i=1}^N \alpha_i \end{aligned}
L(w,b,α)==21∣∣w∣∣2+i=1∑Nαi(1−yi(w⋅xi+b))21∣∣w∣∣2−i=1∑Nαiyi(w⋅xi+b))+i=1∑Nαi
等价为极小极大问题:(参考拉格朗日对偶性的笔记)
min
w
,
b
max
α
L
(
w
,
b
,
α
)
\min_{w,b}\max_{\alpha}L(w,b,\alpha)
w,bminαmaxL(w,b,α)
等价为对应的对偶问题,即极大极小问题:
max
α
min
w
,
b
L
(
w
,
b
,
α
)
\max_{\alpha}\min_{w,b}L(w,b,\alpha)
αmaxw,bminL(w,b,α)
为了求解对偶问题,我们要先求解极小问题,再求解极大问题:
- 求 min w , b L ( w , b , α ) \min\limits_{w,b}L(w,b,\alpha) w,bminL(w,b,α) :由 FOC 得:
∂ L ∂ w = w − ∑ i = 1 N α i y i x i = 0 ⇒ w = ∑ i = 1 N α i y i x i ∂ L ∂ b = − ∑ i = 1 N α i y i = 0 ⇒ ∑ i = 1 N α i y i = 0 \begin{aligned} \frac{\partial L}{\partial w}= &\, w-\sum_{i=1}^{N}\alpha_iy_ix_i=0 \quad\Rightarrow\quad w =\sum_{i=1}^{N}\alpha_iy_ix_i\\ \frac{\partial L}{\partial b}= &\, -\sum_{i=1}^{N}\alpha_iy_i=0 \quad\Rightarrow \quad \sum_{i=1}^{N}\alpha_iy_i=0 \end{aligned} ∂w∂L=∂b∂L=w−i=1∑Nαiyixi=0⇒w=i=1∑Nαiyixi−i=1∑Nαiyi=0⇒i=1∑Nαiyi=0
代回原来的 Lagrangian ,得到:
L
(
w
,
b
,
α
)
=
−
1
2
∑
i
=
1
N
∑
j
=
1
N
α
i
α
j
y
i
y
j
(
x
i
⋅
x
j
)
+
∑
i
=
1
N
α
i
L(w,b,\alpha)=-\frac{1}{2}\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)+\sum\limits_{i=1}^{N}\alpha_i
L(w,b,α)=−21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)+i=1∑Nαi
- 求 max α ( min w , b L ( w , b , α ) ) \max\limits_{\alpha}\left(\min\limits_{w,b}L(w,b,\alpha)\right) αmax(w,bminL(w,b,α)) :我们取个负号,得到对应的对偶优化问题:
min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i s.t. ∑ i = 1 N α i y i = 0 α i ≥ 0 , i = 1 , 2 , ⋯ , N \begin{aligned} \min_{\alpha}&\, \frac{1}{2}\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)-\sum\limits_{i=1}^{N}\alpha_i \\ \text{s.t.}&\,\, \sum_{i=1}^{N}\alpha_iy_i=0 \\ &\,\, \alpha_i\geq 0,\quad i=1,2,\cdots,N \end{aligned} αmins.t.21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)−i=1∑Nαii=1∑Nαiyi=0αi≥0,i=1,2,⋯,N
因此,我们先解决对应的对偶优化问题,得到
α
∗
\alpha^\ast
α∗ ,再带入得到
w
∗
w^\ast
w∗ 和
b
∗
b^\ast
b∗ 。其中
b
∗
b^\ast
b∗ 的计算为:由于对偶优化问题满足 KKT 条件(参考拉格朗日对偶性的笔记),因此有:
α
i
∗
(
y
i
(
w
∗
⋅
x
i
+
b
∗
)
−
1
)
=
0
,
i
=
1
,
2
,
⋯
,
N
\alpha_i^\ast (y_i(w^\ast \cdot x_i+b^\ast)-1)=0,\quad i=1,2,\cdots,N
αi∗(yi(w∗⋅xi+b∗)−1)=0,i=1,2,⋯,N
要么
α
i
∗
=
0
\alpha_i^\ast=0
αi∗=0 ,说明
x
i
x_i
xi 没有起到约束作用;要么
α
i
∗
>
0
\alpha_i^\ast\gt 0
αi∗>0 ,即
x
i
x_i
xi 是支持向量。至少存在一个
a
j
∗
>
0
a_j^\ast\gt 0
aj∗>0 ,此时有:
y
j
(
w
∗
⋅
x
j
+
b
∗
)
−
1
=
0
y_j(w^\ast \cdot x_j +b^\ast)-1=0
yj(w∗⋅xj+b∗)−1=0
代入
w
=
∑
i
=
1
N
α
i
y
i
x
i
w =\sum\limits_{i=1}^{N}\alpha_iy_ix_i
w=i=1∑Nαiyixi ,而且
1
y
j
=
y
j
\frac{1}{y_j}=y_j
yj1=yj ,所以有:
b
∗
=
y
j
−
∑
i
=
1
N
α
i
∗
y
i
b^\ast=y_j-\sum\limits_{i=1}^N \alpha_i^\ast y_i
b∗=yj−i=1∑Nαi∗yi
算法:线性可分支持向量机学习算法 - 最大间隔法 的对偶算法
- 输入:线性可分训练数据集 T = { ( x 1 , t 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } T=\set{(x_1,t_1),(x_2,y_2),\cdots,(x_N,y_N)} T={(x1,t1),(x2,y2),⋯,(xN,yN)} ,其中 x i ∈ X ⊆ R n x_i\in\mathcal{X}\subseteq \R^n xi∈X⊆Rn , y i ∈ Y = { 1 , − 1 } y_i\in\mathcal{Y}=\set{1,\,-1} yi∈Y={1,−1}
- 输出:最大间隔分离超平面和分类决策函数
- 构造并求解约束最优化问题:
min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i s.t. ∑ i = 1 N α i y i = 0 α i ≥ 0 , i = 1 , 2 , ⋯ , N \begin{aligned} \min_{\alpha}&\, \frac{1}{2}\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)-\sum\limits_{i=1}^{N}\alpha_i \\ \text{s.t.}&\,\, \sum_{i=1}^{N}\alpha_iy_i=0 \\ &\,\, \alpha_i\geq 0,\quad i=1,2,\cdots,N \end{aligned} αmins.t.21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)−i=1∑Nαii=1∑Nαiyi=0αi≥0,i=1,2,⋯,N
得到最优解 α ∗ \alpha^\ast α∗ ;
- 计算:
w ∗ = ∑ i = 1 N α i ∗ y i x i w^\ast = \sum\limits_{i=1}^{N}\alpha_i^\ast y_ix_i w∗=i=1∑Nαi∗yixi
并选择
α
∗
\alpha^\ast
α∗ 的一个正分量
α
j
∗
\alpha_j^\ast
αj∗ ,计算:
b
∗
=
y
j
−
∑
i
=
1
N
α
i
∗
y
i
(
x
i
⋅
x
j
)
b^\ast=y_j-\sum\limits_{i=1}^{N}\alpha_i^\ast y_i(x_i\cdot x_j)
b∗=yj−i=1∑Nαi∗yi(xi⋅xj)
- 由此得到分离超平面:
w ∗ ⋅ x + b ∗ = 0 w^\ast \cdot x+b^\ast = 0 w∗⋅x+b∗=0
分类决策函数:
f
(
x
)
=
sign
(
w
∗
⋅
x
+
b
∗
)
f(x)=\text{sign}(w^\ast \cdot x+b^\ast)
f(x)=sign(w∗⋅x+b∗)
线性支持向量机与软间隔最大化
线性支持向量机不要求数据集线性可分,仅仅是支持向量机的数学形式是线性的。
定义
线性支持向量机:对于给定的线性不可分的训练数据集,通过软间隔最大化问题或对应的凸二次规划问题,得到的分离超平面为:
w
∗
⋅
x
+
b
∗
=
0
w^\ast \cdot x+b^\ast=0
w∗⋅x+b∗=0
以及相应的分类决策函数:
f
(
x
)
=
sign
(
w
∗
⋅
x
+
b
∗
)
f(x)=\text{sign}(w^\ast \cdot x+b^\ast)
f(x)=sign(w∗⋅x+b∗)
称为线性支持向量机。
软间隔最大化
软间隔最大化:软间隔的思想是,对于非线性可分的数据集,只是存在一些特异点(outlier),将这些特异点去除后数据集就变得线性可分了。那么,特异点不能满足函数间隔大于等于 1 的约束条件,我们需要引入新的变量:
松弛变量:每个样本引入一个松弛变量
ξ
i
≥
0
\xi_i \geq 0
ξi≥0 ,使得约束条件变为:
y
i
(
w
⋅
x
i
+
b
)
≥
1
−
ξ
i
y_i(w\cdot x_i + b) \geq 1-\xi_i
yi(w⋅xi+b)≥1−ξi
惩罚参数:对于分类问题,我们是想让尽量多的样本点处于间隔之外,所以松弛变量应当尽可能小,需要对松弛变量支付代价,目标函数变为:
1
2
∣
∣
w
∣
∣
2
+
C
∑
i
=
1
N
ξ
i
\frac{1}{2}||w||^2+C\sum\limits_{i=1}^{N}\xi_i
21∣∣w∣∣2+Ci=1∑Nξi
其中惩罚参数
C
>
0
C\gt 0
C>0 ,是 SVM 的超参数之一。
算法:线性支持向量机学习算法 - 最大间隔法
- 输入:非线性可分训练数据集 T = { ( x 1 , t 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } T=\set{(x_1,t_1),(x_2,y_2),\cdots,(x_N,y_N)} T={(x1,t1),(x2,y2),⋯,(xN,yN)} ,其中 x i ∈ X ⊆ R n x_i\in\mathcal{X}\subseteq \R^n xi∈X⊆Rn , y i ∈ Y = { 1 , − 1 } y_i\in\mathcal{Y}=\set{1,\,-1} yi∈Y={1,−1}
- 输出:最大间隔分离超平面和分类决策函数
- 构造并求解约束最优化问题:
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 N ξ i s.t. y i ( w ⋅ x i + b ) ≥ 1 − ξ i , i = 1 , 2 , ⋯ , N ξ i ≥ 0 , i = 1 , 2 , ⋯ , N \begin{aligned} \min\limits_{w,\,b}&\, \frac{1}{2}||w||^2+C\sum\limits_{i=1}^{N}\xi_i \\ \text{s.t.}&\,\, y_i(w \cdot x_i+b) \geq 1-\xi_i,\quad i=1,2,\cdots,N \\ &\,\,\xi_i \geq 0 ,\quad i=1,2,\cdots,N \\ \end{aligned} w,bmins.t.21∣∣w∣∣2+Ci=1∑Nξiyi(w⋅xi+b)≥1−ξi,i=1,2,⋯,Nξi≥0,i=1,2,⋯,N
求得最优解 w ∗ w^\ast w∗ , b ∗ b^\ast b∗ ;
- 由此得到分离超平面:
w ∗ ⋅ x + b ∗ = 0 w^\ast \cdot x+b^\ast = 0 w∗⋅x+b∗=0
分类决策函数:
f
(
x
)
=
sign
(
w
∗
⋅
x
+
b
∗
)
f(x)=\text{sign}(w^\ast \cdot x+b^\ast)
f(x)=sign(w∗⋅x+b∗)
对偶算法
对偶算法的推导:软间隔最大化问题的 Lagrangian 为:
L
(
w
,
b
,
ξ
,
α
,
μ
)
=
1
2
∣
∣
w
∣
∣
2
+
C
∑
i
=
1
N
ξ
i
+
∑
i
=
1
N
α
i
(
1
−
ξ
i
−
y
i
(
w
⋅
x
i
+
b
)
)
−
∑
i
=
1
N
μ
i
ξ
i
=
1
2
∣
∣
w
∣
∣
2
+
C
∑
i
=
1
N
ξ
i
−
∑
i
=
1
N
α
i
y
i
(
w
⋅
x
i
+
b
)
)
+
∑
i
=
1
N
α
i
−
∑
i
=
1
N
(
α
i
+
μ
i
)
ξ
i
\begin{aligned} L(w,b,\xi,\alpha,\mu)=&\, \frac{1}{2}||w||^2+C\sum\limits_{i=1}^{N}\xi_i+ \sum\limits_{i=1}^N \alpha_i(1-\xi_i-y_i(w\cdot x_i+b))-\sum\limits_{i=1}^{N}\mu_i\xi_i \\ =&\, \frac{1}{2}||w||^2+C\sum\limits_{i=1}^{N}\xi_i-\sum\limits_{i=1}^N \alpha_iy_i(w\cdot x_i+b))+\sum\limits_{i=1}^N \alpha_i-\sum\limits_{i=1}^{N}(\alpha_i+\mu_i)\xi_i \end{aligned}
L(w,b,ξ,α,μ)==21∣∣w∣∣2+Ci=1∑Nξi+i=1∑Nαi(1−ξi−yi(w⋅xi+b))−i=1∑Nμiξi21∣∣w∣∣2+Ci=1∑Nξi−i=1∑Nαiyi(w⋅xi+b))+i=1∑Nαi−i=1∑N(αi+μi)ξi
等价为极小极大问题:(参考拉格朗日对偶性的笔记)
min
w
,
b
,
ξ
max
α
,
μ
L
(
w
,
b
,
ξ
,
α
,
μ
)
\min_{w,b,\xi}\max_{\alpha,\mu}L(w,b,\xi,\alpha,\mu)
w,b,ξminα,μmaxL(w,b,ξ,α,μ)
等价为对应的对偶问题,即极大极小问题:
max
α
,
μ
min
w
,
b
,
ξ
L
(
w
,
b
,
ξ
,
α
,
μ
)
\max_{\alpha,\mu}\min_{w,b,\xi}L(w,b,\xi,\alpha,\mu)
α,μmaxw,b,ξminL(w,b,ξ,α,μ)
为了求解对偶问题,我们要先求解极小问题,再求解极大问题:
- 求 min w , b , ξ L ( w , b , ξ , α , μ ) \min\limits_{w,b,\xi}L(w,b,\xi,\alpha,\mu) w,b,ξminL(w,b,ξ,α,μ) :由 FOC 得:
∂ L ∂ w = w − ∑ i = 1 N α i y i x i = 0 ⇒ w = ∑ i = 1 N α i y i x i ∂ L ∂ b = − ∑ i = 1 N α i y i = 0 ⇒ ∑ i = 1 N α i y i = 0 ∂ L ∂ ξ i = C − α i − μ i = 0 \begin{aligned} \frac{\partial L}{\partial w}= &\, w-\sum_{i=1}^{N}\alpha_iy_ix_i=0 \quad\Rightarrow\quad w =\sum_{i=1}^{N}\alpha_iy_ix_i\\ \frac{\partial L}{\partial b}= &\, -\sum_{i=1}^{N}\alpha_iy_i=0 \quad\Rightarrow \quad \sum_{i=1}^{N}\alpha_iy_i=0 \\ \frac{\partial L}{\partial \xi_i}=&\, C-\alpha_i-\mu_i=0 \end{aligned} ∂w∂L=∂b∂L=∂ξi∂L=w−i=1∑Nαiyixi=0⇒w=i=1∑Nαiyixi−i=1∑Nαiyi=0⇒i=1∑Nαiyi=0C−αi−μi=0
代回原来的 Lagrangian ,得到(这个结果和前面的硬间隔最大化的结果是一样的,已经没有
μ
\mu
μ 了):
L
(
w
,
b
,
α
)
=
−
1
2
∑
i
=
1
N
∑
j
=
1
N
α
i
α
j
y
i
y
j
(
x
i
⋅
x
j
)
+
∑
i
=
1
N
α
i
L(w,b,\alpha)=-\frac{1}{2}\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)+\sum\limits_{i=1}^{N}\alpha_i
L(w,b,α)=−21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)+i=1∑Nαi
- 求 max α , μ ( min w , b , ξ L ( w , b , ξ , α , μ ) ) \max\limits_{\alpha,\mu}\left(\min\limits_{w,b,\xi}L(w,b,\xi,\alpha,\mu)\right) α,μmax(w,b,ξminL(w,b,ξ,α,μ)) :我们取个负号,得到对应的对偶优化问题:
min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i s.t. ∑ i = 1 N α i y i = 0 C − α i − μ i = 0 α i ≥ 0 μ i ≥ 0 , i = 1 , 2 , ⋯ , N \begin{aligned} \min_{\alpha}&\, \frac{1}{2}\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)-\sum\limits_{i=1}^{N}\alpha_i \\ \text{s.t.}&\,\, \sum_{i=1}^{N}\alpha_iy_i=0 \\ &\,\, C-\alpha_i-\mu_i=0 \\ &\,\, \alpha_i\geq 0 \\ &\,\, \mu_i \geq 0,\quad i=1,2,\cdots,N \\ \end{aligned} αmins.t.21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)−i=1∑Nαii=1∑Nαiyi=0C−αi−μi=0αi≥0μi≥0,i=1,2,⋯,N
w
∗
w^\ast
w∗ 和
b
∗
b^\ast
b∗ 的计算跟前面硬间隔最大化是一样的。既然这里已经没有
μ
i
\mu_i
μi 了,因此
α
i
\alpha_i
αi 的取值范围实际上可以写成:
0
≤
α
i
≤
C
0 \leq \alpha_i \leq C
0≤αi≤C
也就是说,软间隔最大化的对偶算法相比于硬间隔最大化中的对偶算法,只多了一个
α
i
\alpha_i
αi 的约束条件:不大于 C。
支持向量:同样地:
-
若 α i = 0 \alpha_i=0 αi=0 ,则样本点 x i x_i xi 落在间隔外;
-
若 0 < α i < C 0\lt \alpha_i \lt C 0<αi<C ,则样本点 x i x_i xi 为支持向量;
-
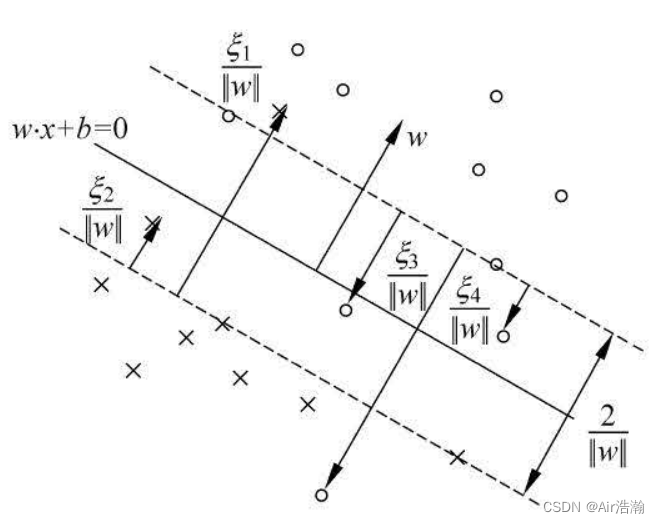
若 α i = C \alpha_i=C αi=C ,则样本点 x i x_i xi 落在间隔内(也可以称为支持向量),此时:
- 若 ξ i = 0 \xi_i =0 ξi=0 ,则样本点 x i x_i xi 落在正确的间隔边界上;
- 若 0 < ξ i < 1 0\lt \xi_i \lt 1 0<ξi<1 ,则样本点 x i x_i xi 落在分离超平面与正确的间隔边界之间;
- 若 ξ i = 0 \xi_i =0 ξi=0 ,则样本点 x i x_i xi 落在分离超平面上;
- 若 ξ i > 1 \xi_i\gt 1 ξi>1 ,则样本点 x i x_i xi 落在分离超平面与错误的间隔边界之间;
样本 x i x_i xi 到间隔边界的距离为 ξ i ∣ ∣ w ∣ ∣ \frac{\xi_i}{||w||} ∣∣w∣∣ξi :
算法:线性支持向量机学习算法 - 最大间隔法 的对偶算法
- 输入:线性可分训练数据集 T = { ( x 1 , t 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } T=\set{(x_1,t_1),(x_2,y_2),\cdots,(x_N,y_N)} T={(x1,t1),(x2,y2),⋯,(xN,yN)} ,其中 x i ∈ X ⊆ R n x_i\in\mathcal{X}\subseteq \R^n xi∈X⊆Rn , y i ∈ Y = { 1 , − 1 } y_i\in\mathcal{Y}=\set{1,\,-1} yi∈Y={1,−1}
- 输出:最大间隔分离超平面和分类决策函数
- 确定超参数:惩罚参数 C > 0 C\gt 0 C>0 ;构造并求解约束最优化问题:
min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i s.t. ∑ i = 1 N α i y i = 0 0 ≤ α i ≤ C , i = 1 , 2 , ⋯ , N \begin{aligned} \min_{\alpha}&\, \frac{1}{2}\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)-\sum\limits_{i=1}^{N}\alpha_i \\ \text{s.t.}&\,\, \sum_{i=1}^{N}\alpha_iy_i=0 \\ &\,\, 0\leq\alpha_i\leq C,\quad i=1,2,\cdots,N \end{aligned} αmins.t.21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)−i=1∑Nαii=1∑Nαiyi=00≤αi≤C,i=1,2,⋯,N
得到最优解 α ∗ \alpha^\ast α∗ ;
- 计算:
w ∗ = ∑ i = 1 N α i ∗ y i x i w^\ast = \sum\limits_{i=1}^{N}\alpha_i^\ast y_ix_i w∗=i=1∑Nαi∗yixi
并选择
α
∗
\alpha^\ast
α∗ 的一个分量
0
<
α
j
∗
<
C
0\lt \alpha_j^\ast\lt C
0<αj∗<C ,计算:
b
∗
=
y
j
−
∑
i
=
1
N
α
i
∗
y
i
(
x
i
⋅
x
j
)
b^\ast=y_j-\sum\limits_{i=1}^{N}\alpha_i^\ast y_i(x_i\cdot x_j)
b∗=yj−i=1∑Nαi∗yi(xi⋅xj)
- 由此得到分离超平面:
w ∗ ⋅ x + b ∗ = 0 w^\ast \cdot x+b^\ast = 0 w∗⋅x+b∗=0
分类决策函数:
f
(
x
)
=
sign
(
w
∗
⋅
x
+
b
∗
)
f(x)=\text{sign}(w^\ast \cdot x+b^\ast)
f(x)=sign(w∗⋅x+b∗)
合页损失函数
线性支持向量机学习还可以解释为:最小化以下目标函数:
∑
i
=
1
N
[
1
−
y
i
(
w
⋅
x
i
+
b
)
]
+
+
λ
∣
∣
w
∣
∣
2
\sum\limits_{i=1}^{N}\left[1-y_i(w\cdot x_i+b)\right]_++\lambda ||w||^2
i=1∑N[1−yi(w⋅xi+b)]++λ∣∣w∣∣2
- 第一项是经验损失或经验风险函数,称为合页损失函数 (下标 + + + 代表 ReLU):
L ( y ( w ⋅ x + b ) ) = [ 1 − y ( w ⋅ x + b ) ] + L(y(w\cdot x+b))=\left[1-y(w\cdot x+b)\right]_+ L(y(w⋅x+b))=[1−y(w⋅x+b)]+
- 第二项则是 L2 正则化项;
Th 7.4:线性支持向量机原始最优化问题:
min
w
,
b
1
2
∣
∣
w
∣
∣
2
+
C
∑
i
=
1
N
ξ
i
s.t.
y
i
(
w
⋅
x
i
+
b
)
≥
1
−
ξ
i
,
i
=
1
,
2
,
⋯
,
N
ξ
i
≥
0
,
i
=
1
,
2
,
⋯
,
N
\begin{aligned} \min\limits_{w,\,b}&\, \frac{1}{2}||w||^2+C\sum\limits_{i=1}^{N}\xi_i \\ \text{s.t.}&\,\, y_i(w \cdot x_i+b) \geq 1-\xi_i,\quad i=1,2,\cdots,N \\ &\,\,\xi_i \geq 0 ,\quad i=1,2,\cdots,N \\ \end{aligned}
w,bmins.t.21∣∣w∣∣2+Ci=1∑Nξiyi(w⋅xi+b)≥1−ξi,i=1,2,⋯,Nξi≥0,i=1,2,⋯,N
等价于最优化问题:
min
w
,
b
∑
i
=
1
N
[
1
−
y
i
(
w
⋅
x
i
+
b
)
]
+
+
λ
∣
∣
w
∣
∣
2
\min\limits_{w,b}\sum\limits_{i=1}^{N}\left[1-y_i(w\cdot x_i+b)\right]_++\lambda ||w||^2
w,bmini=1∑N[1−yi(w⋅xi+b)]++λ∣∣w∣∣2
证明:令
ξ
i
=
[
1
−
y
i
(
w
⋅
x
i
+
b
)
]
+
\xi_i=\left[1-y_i(w\cdot x_i+b)\right]_+
ξi=[1−yi(w⋅xi+b)]+ ,则
ξ
i
≥
0
\xi_i \geq 0
ξi≥0 成立,且
y
i
(
w
⋅
x
i
+
b
)
≥
1
−
ξ
i
y_i(w \cdot x_i+b) \geq 1-\xi_i
yi(w⋅xi+b)≥1−ξi 成立。所以新的优化问题可以写成:
min
w
,
b
∑
i
=
1
N
ξ
i
+
λ
∣
∣
w
∣
∣
2
\min\limits_{w,b}\sum\limits_{i=1}^{N}\xi_i+\lambda ||w||^2
w,bmini=1∑Nξi+λ∣∣w∣∣2
取
λ
=
1
2
C
\lambda=\frac{1}{2C}
λ=2C1 ,则变为:
min
w
,
b
1
C
(
1
2
∣
∣
w
∣
∣
2
+
C
∑
i
=
1
N
ξ
i
)
\min\limits_{w,\,b}\, \frac{1}{C}\left(\frac{1}{2}||w||^2+C\sum\limits_{i=1}^{N}\xi_i\right)
w,bminC1(21∣∣w∣∣2+Ci=1∑Nξi)
和原始最优化问题等价。
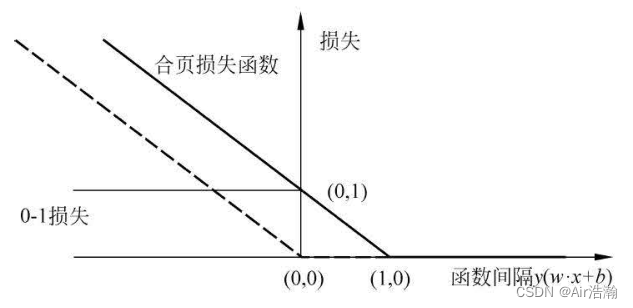
代理损失函数:图中展示了 0-1 损失函数和合页损失函数。可以认为为 0-1 损失函数是二分类问题真正的损失函数,而合页损失函数是 0-1 损失函数的一个上界,称为代理损失函数。
虚线是感知机的损失函数,可以看出在 [ 0 , 1 ) [0,\,1) [0,1) 区间内,合页损失函数仍有损失,而感知机的损失函数已经是 0 了,说明感知机只要要求分类正确即可,而合页损失函数需要在分类正确的前提下,确信度足够高(即样本位于间隔之外),才能没有损失。