欧拉筛(Euler's Sieve)(又叫线性筛)是一种用于生成素数的高效算法。与传统的试除法不同,欧拉筛通过线性时间复杂度来筛选出一定范围内的素数。这个算法以瑞士数学家莱昂哈德·欧拉(Leonhard Euler)的名字命名,尽管他并没有发明这个算法,但他对素数研究的贡献使得这个算法以他的名字命名.
使用完欧拉筛后,n范围内的所有素数都会存放到prime表中,如果要输出n范围内所有的素数,则把prime表中的所有内容输出即可。
欧拉筛的基本思想是从小到大逐个筛掉合数,最终剩下的就是素数。与试除法不同,欧拉筛通过每个合数仅被筛一次来实现高效率。算法的步骤如下:
初始化工作:
1.初始化一个bool 数组isprime,其中isprime[i] 表示 自然数i是否为素数.
2.初始化一个int数组 prime,用来保存所有的素数.
3.初始化int类型的n,表示筛选范围n以内的所有素数.
4.初始化int类型的cnt,表示当前筛选的素数的个数,同时作为prime下标来进行不断填充。
5.因为自然数 1 不是素数,所以先把 isprime[1] = false;
算法操作:
首先 i 从 2 开始 循环遍历到 n,对于每一次循环,首先判断isprime[i]是否为true,若为true,说明 i 为素数,将 i 加入到prime数组中,即prime[++cnt] = i;否则不用添加。
接下来开始筛合数(本质是将对应的标志位设为false), i 的倍数一定是合数,倍数应该为 prime[j]倍,所以再有一个循环,从 j=1 到 cnt(即当前prime的大小) 同时要求i*prime[j] <n,因为数据范围就是n;然后将isprime[ i*prime[j] ] = false.
接下来,有个难点是(我可能讲不清楚,因为确实单凭看文字不好理解,我建议大家可以去b站看一下这个视频欧拉筛图解,这个把欧拉筛的过程完整的展示了一下,包括这个难点,我感觉非常不错,建议大家可以看一看)
当 i % prime[j] == 0时,就要立即退出该循环,不要再继续筛合数了。
这是因为我们要筛选的是 i 的最小质倍数,假设此时i = 12,此时prime数组中应为[0,2,3,5,7,11],首先j = 1, prime[j] = 2; isprime[i*prime[j]] = false,即将12*2=24筛掉,但如果此时我们不退出该循环,而是继续筛选,j=2,prime[j] = 3,isprime[i*prime[j]] = false,即将12*3=36筛掉,那么当i=18时,j=1,prime[j] = 2,isprime[i*prime[j]] = false,又将18*2=36筛了一次,造成效率下降。违背我们上面所说的“每个合数仅被筛一次”。所以当 i % prime[j] == 0时,就要立即退出该循环。
代码如下:
void Euler(int n) {
vector<bool> isprime(n+1,true);//isprime[i]表示第i个数是否为素数
vector<int> prime(n);//存放的素数
int cnt = 0;//筛出的质数个数
isprime[1] = false;//1不是素数,先将1置为false
for(int i = 2; i < n; i++)
{
//如果i为素数,则将其添加到prime当中
if(isprime[i]) prime[++cnt] = i;
for(int j = 1; j <= cnt && i * prime[j] <= n; j++)
{
//将筛选到的合数置为false
isprime[i*prime[j]] = false;
//点睛之笔,如果% == 0,说明当前prime[j]就是最小质倍数,退出当前循环
if(i % prime[j] == 0) break;
}
}
}同时大家可以做一下leetcode上204题:204. 计数质数 ,只需要最后将cnt返回即可。
到这里欧拉筛的过程就结束了。至于证明和正确性什么的,有兴趣的可以去网上阅读相关资料查询,这里就不多讲解了~
这里可以测试一下:
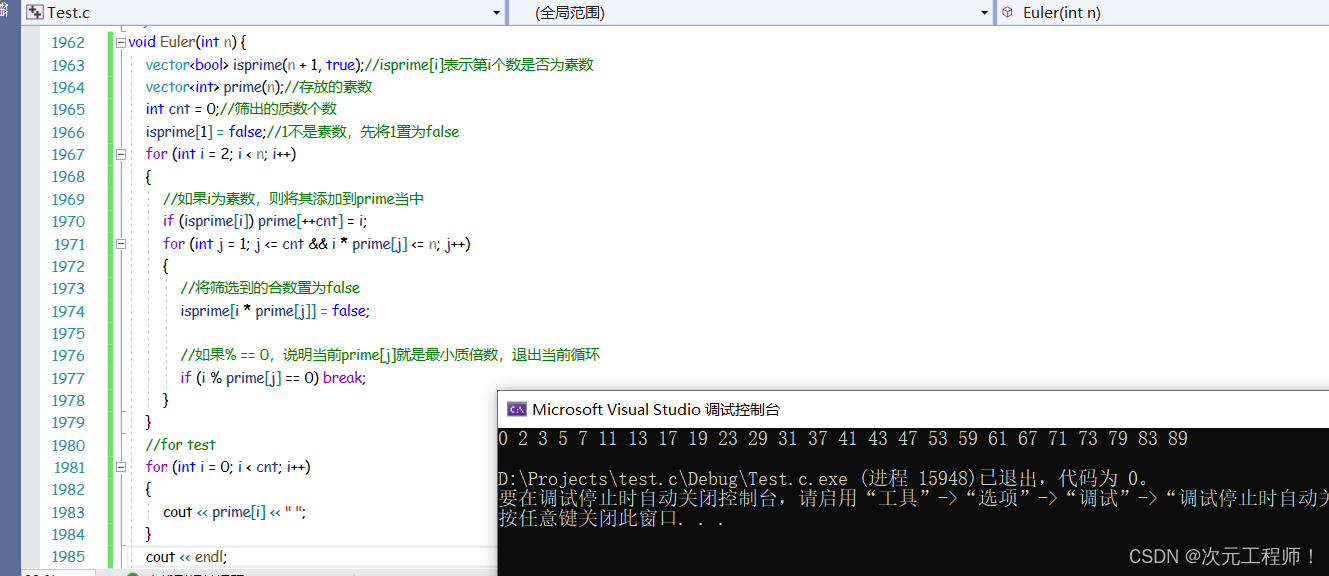
很完美的输出了出来。
如果想在外面输出,可以将那几个变量设置为全局的,然后再进行操作和访问。