目录标题
- 离散XXX
- Q1 离散化的表达式和传递函数怎么匹配上?
- 离散系统的分析与校正
- Q ZOH有什么作用
- K ZOH的Z变换✨
- K Z变换表格
- 模拟化矫正
- ZOH的等效
- Q 为什么离散化之后幅值会变化?
- Q 模拟化校正中ZOH环节为什么需要等效成惯性环节?
- 离散化的方法
- Q 阶跃响应不变法串联ZOH有什么作用,如果不串联会怎么样?
- Q 为什么大多数情况下,我们用的是双线性匹配法而不是Z变换,难道Z变换不是效果最好的?
- 矫正系统的设计
- Q 通常采用什么校正方法进行设计?
- 数字化校正:最小拍设计
- Q 做题时的已知量,未知量分别是什么?
- 系统介绍✨
- 经典输入信号的离散化
- 矫正系统设计思路✨
- 开环传函的单位圆上及圆外零极点处理
- 无纹波最小拍设计
- 总结:做题步骤✨✨
- 补充:无纹波最小拍系统设计
- 无纹波判断方法
- 无纹波设计思路
Q 代表帮助理解概念的问题
K 代表梳理过程中零碎的知识点
U 代表未解决的问题
离散XXX
Q1 离散化的表达式和传递函数怎么匹配上?
离散系统的分析与校正
Q ZOH有什么作用
K ZOH的Z变换✨
串联零阶保持器后:
G
(
z
)
=
(
1
−
z
−
1
)
Z
[
G
0
(
s
)
s
]
G(z)=(1-z^{-1})Z[\frac{G_0(s)}{s}]
G(z)=(1−z−1)Z[sG0(s)]
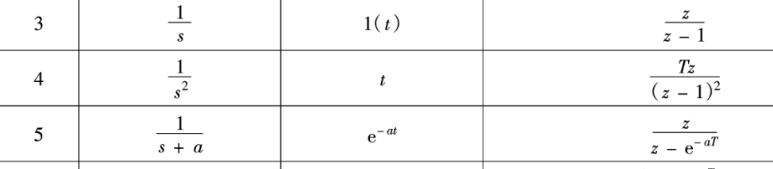
K Z变换表格
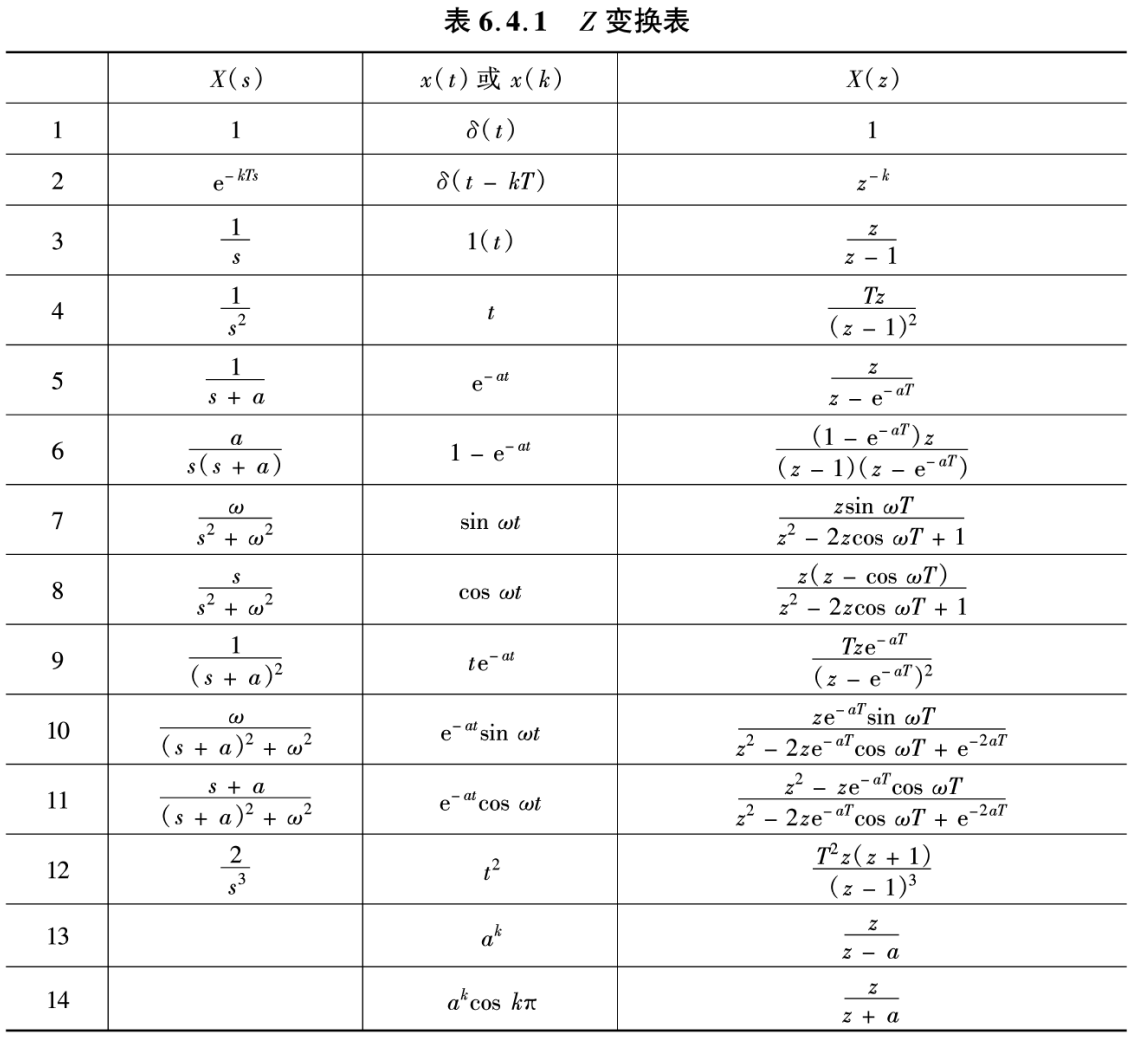
模拟化矫正
先在s域进行校正,随后在用不同方法转到离散域
需要注意的是:
- ZOH环节的等效,该环节带来的相角损失等,需要进行一定的等效
- 离散化的方法:有一阶差分近似法,阶跃响应不变法,根匹配法和双线性匹配法【较常用】
ZOH的等效
用泰勒展开,可以得到
e
−
T
s
=
e
−
T
2
s
e
T
2
s
=
1
−
T
s
2
+
(
T
s
)
2
8
−
(
T
s
)
3
48
+
⋯
1
+
T
s
2
+
(
T
s
)
2
8
+
(
T
s
)
3
48
+
⋯
≈
1
−
T
s
2
1
+
T
s
2
\begin{array}{l} e^{-T s}=\frac{e^{-\frac{T}{2} s}}{e^{\frac{T}{2} s}}=\frac{1-\frac{T s}{2}+\frac{(T s)^{2}}{8}-\frac{(T s)^{3}}{48}+\cdots}{1+\frac{T s}{2}+\frac{(T s)^{2}}{8}+\frac{(T s)^{3}}{48}+\cdots} \approx \frac{1-\frac{T s}{2}}{1+\frac{T s}{2}} \end{array}
e−Ts=e2Tse−2Ts=1+2Ts+8(Ts)2+48(Ts)3+⋯1−2Ts+8(Ts)2−48(Ts)3+⋯≈1+2Ts1−2Ts
因此
1
−
e
−
T
s
s
≈
T
T
2
s
+
1
\frac{1-e^{-T s}}{s} \approx \frac{T}{\frac{T}{2} s+1}
s1−e−Ts≈2Ts+1T
但是离散化之后,系统的幅值变成原来幅值的
1
T
\frac{1}{T}
T1倍,因此为了恢复成原来的幅值,上面的
T
T
T项被抵消。
Q 为什么离散化之后幅值会变化?
Q 模拟化校正中ZOH环节为什么需要等效成惯性环节?
ZOH环节是零阶保持器,为了让响应保持住。需要等效是因为ZOH环节是滞后环节,不方便考虑,但是对应着相角损失,在设计系统是应该被纳入考量
离散化的方法
- 一阶差分近似法
D ( z ) = D ( s ) ∣ s = 1 − z − 1 T D(z)=\left.D(s)\right|_{s=\frac{1-z^{-1}}{T}} D(z)=D(s)∣s=T1−z−1 - 阶跃响应不变法
是通过串联一个虚拟的零阶保持器后进行Z变换,得到 D ( s ) D(s) D(s)的离散形式 D ( z ) D(z) D(z)
D ( z ) = Z [ 1 − e − T s s D ( s ) ] D(z)=Z\left[\frac{1-e^{-T s}}{s} D(s)\right] D(z)=Z[s1−e−TsD(s)] - 根匹配法
( s + a ) → ( 1 − e − a T z − 1 ) (s+a) \rightarrow\left(1-e^{-a T} z^{-1}\right) (s+a)→(1−e−aTz−1) - 双线性匹配法
D ( z ) = D ( s ) ∣ s = 2 T z − 1 z + 1 D(z)=\left.D(s)\right|_{s=\frac{2}{T} \frac{z-1}{z+1}} D(z)=D(s)∣s=T2z+1z−1
Q 阶跃响应不变法串联ZOH有什么作用,如果不串联会怎么样?
Q 为什么大多数情况下,我们用的是双线性匹配法而不是Z变换,难道Z变换不是效果最好的?
矫正系统的设计
在s域进行设计。
Q 通常采用什么校正方法进行设计?
数字化校正:最小拍设计
其目的是:(在离散域中)用尽可能少的拍数,跟上系统
Q 做题时的已知量,未知量分别是什么?
开环传函
G
(
s
)
G(s)
G(s)(或者
G
(
z
)
G(z)
G(z))是已知量,要求的是矫正部分
G
D
(
z
)
G_D(z)
GD(z)
通过选择合适的闭环传函
Φ
(
z
)
\Phi(z)
Φ(z)和误差传函
Φ
e
(
z
)
\Phi_e(z)
Φe(z)来确定
系统介绍✨
如图,矫正部分为
G
D
(
z
)
G_D(z)
GD(z)
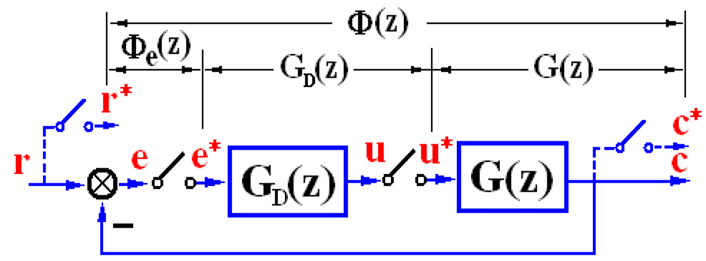
由流程图关系,有:
G
D
(
s
)
=
Φ
(
z
)
Φ
e
(
z
)
⋅
G
(
z
)
G_D(s) = \frac{\Phi(z)}{\Phi_e(z)\cdot G(z)}
GD(s)=Φe(z)⋅G(z)Φ(z)
推导过程【很简单的!】:
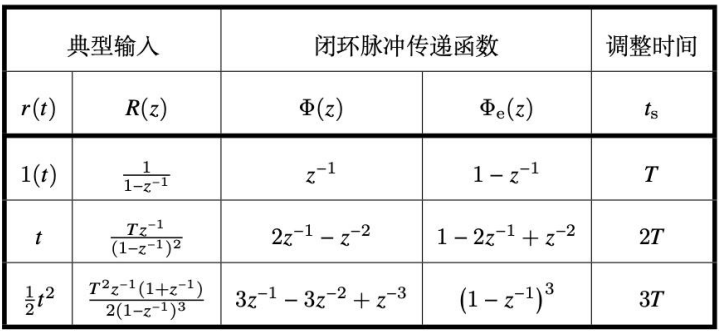
经典输入信号的离散化
R
(
z
)
=
{
z
z
−
1
=
1
1
−
z
−
1
【
r
(
t
)
=
1
(
t
)
】
T
z
(
z
−
1
)
2
=
T
z
−
1
(
1
−
z
−
1
)
2
【
r
(
t
)
=
t
】
T
2
z
(
z
+
1
)
2
(
z
−
1
)
3
=
T
2
z
−
1
(
1
+
z
−
1
)
2
(
1
−
z
−
1
)
3
【
r
(
t
)
=
t
2
2
】
R(z)=\left\{\begin{array}{l} \frac{z}{z-1}=\frac{1}{1-z^{-1}} &【r(t) = 1(t)】\\ \frac{T z}{(z-1)^{2}}=\frac{T z^{-1}}{\left(1-z^{-1}\right)^{2}} &【r(t) = t】\\ \frac{T^{2} z(z+1)}{2(z-1)^{3}}=\frac{T^{2} z^{-1}\left(1+z^{-1}\right)}{2\left(1-z^{-1}\right)^{3}}&【r(t) = \frac{t^2}{2}】 \end{array}\right.
R(z)=⎩
⎨
⎧z−1z=1−z−11(z−1)2Tz=(1−z−1)2Tz−12(z−1)3T2z(z+1)=2(1−z−1)3T2z−1(1+z−1)【r(t)=1(t)】【r(t)=t】【r(t)=2t2】
统一表示为
R
(
z
)
=
A
(
z
)
(
1
−
z
−
1
)
m
R(z)=\frac{A(z)}{\left(1-z^{-1}\right)^{m}}
R(z)=(1−z−1)mA(z)
矫正系统设计思路✨
如果一开始是s域,那么通过z变换变到z域【有ZOH也正常做】,得到Z域的开环传函 G ( z ) G(z) G(z)
按照设计思路,在不同的输入
R
(
z
)
R(z)
R(z)下,应该让
e
(
∞
T
)
=
0
e(\infty T)=0
e(∞T)=0,由终值定理
E
(
z
)
=
Φ
e
(
z
)
⋅
R
(
z
)
=
A
(
z
)
(
1
−
z
−
1
)
m
Φ
e
(
z
)
e
(
∞
T
)
=
lim
z
→
1
(
z
−
1
)
A
(
z
)
(
1
−
z
−
1
)
m
Φ
e
(
z
)
=
0
\begin{array}{l} E(z)=\Phi_{e}(z) \cdot R(z)=\frac{A(z)}{\left(1-z^{-1}\right)^{m}} \Phi_{e}(z) \\ e(\infty T)=\lim _{z \rightarrow 1}\left(z-1\right) \frac{A(z)}{\left(1-z^{-1}\right)^{m}} \Phi_{e}(z)=0 \end{array}
E(z)=Φe(z)⋅R(z)=(1−z−1)mA(z)Φe(z)e(∞T)=limz→1(z−1)(1−z−1)mA(z)Φe(z)=0
因此,对
Φ
e
(
z
)
\Phi_e(z)
Φe(z)的结构有一定的要求,即
Φ
e
(
z
)
=
(
1
−
z
−
1
)
m
F
(
z
)
=
F
(
z
)
=
1
(
1
−
z
−
1
)
m
\Phi_{e}(z)=\left(1-z^{-1}\right)^{m} F(z) \stackrel{F(z)=1}{=}\left(1-z^{-1}\right)^{m}
Φe(z)=(1−z−1)mF(z)=F(z)=1(1−z−1)m
如以上公式所示,就是模拟了最简单的情况,令
F
(
z
)
=
1
F(z)=1
F(z)=1
设计出
Φ
e
(
z
)
\Phi_e(z)
Φe(z)之后,由
Φ
(
z
)
=
1
−
Φ
e
(
z
)
\Phi(z)=1-\Phi_e(z)
Φ(z)=1−Φe(z)得到闭环传函和闭环误差传函
开环传函的单位圆上及圆外零极点处理
上述情况假设了开环传函
G
(
z
)
G(z)
G(z)没有单位圆上及单位圆外的零极点。
如果开环传函
G
(
z
)
G(z)
G(z)存在不稳定零极点,则需要在
F
(
z
)
F(z)
F(z)上做一些操作,实现零极点对消
其中:
Φ
e
(
z
)
\Phi_e(z)
Φe(z)的零点应该包括
G
(
z
)
G(z)
G(z)中不稳定的极点
Φ
(
z
)
\Phi(z)
Φ(z)的零点应该包括
G
(
z
)
G(z)
G(z)中不稳定的零点及
G
(
z
)
G(z)
G(z)中的纯延迟环节【
z
−
1
z^{-1}
z−1】
那么,为了满足
Φ
(
z
)
=
1
−
Φ
e
(
z
)
\Phi(z)=1-\Phi_e(z)
Φ(z)=1−Φe(z),需要一定的待定系数法。
无纹波最小拍设计
总结:做题步骤✨✨
格式:常为首1【
1
±
k
z
−
1
1\pm k z^{-1}
1±kz−1】
第一步:得到z域的开环传函
可能需要离散化
用到的方法:留数法拆传函、零阶保持器Z变换、Z变换公式
G ( z ) = ( 1 − z − 1 ) Z [ G 0 ( s ) s ] G(z)=(1-z^{-1})Z[\frac{G_0(s)}{s}] G(z)=(1−z−1)Z[sG0(s)]
第二步:检查开环传函
- 传递函数中有没有单位圆上或者圆外的零极点
零点放到 Φ ( z ) \Phi(z) Φ(z) 极点放到 Φ e ( z ) \Phi_e(z) Φe(z),然后为了保证阶数【必须满足 Φ ( z ) = 1 − Φ e ( z ) \Phi(z)=1-\Phi_e(z) Φ(z)=1−Φe(z)】,在零/极点进行待定系数法补偿。
注意,待定系数法的同时也应该进行比例系数补偿K,通常放到闭环传函 Φ ( z ) \Phi(z) Φ(z)中 - 传递函数中有没有纯延迟环节
z
−
1
z^{-1}
z−1
如果有,那么闭环传函 Φ ( z ) \Phi(z) Φ(z)中也应存在该环节
第三步:确定闭环传函和误差闭环传函
在第三步两个特殊情况都没有的情况下,误差传函为
Φ
e
(
z
)
=
(
1
−
z
−
1
)
v
+
1
\Phi_{e}(z)=\left(1-z^{-1}\right)^{v+1}
Φe(z)=(1−z−1)v+1
v为系统型别【 r ( t ) = t v r(t)=t^v r(t)=tv】
第四步:确定校正系统传函
根据两个传函和开环传函,确定校正系统传函
G
D
(
s
)
=
Φ
(
z
)
Φ
e
(
z
)
⋅
G
(
z
)
G_D(s) = \frac{\Phi(z)}{\Phi_e(z)\cdot G(z)}
GD(s)=Φe(z)⋅G(z)Φ(z)
第五步:得到校正后的误差传函
E
′
(
z
)
=
G
D
(
z
)
⋅
E
(
z
)
=
G
D
(
z
)
⋅
Φ
e
(
z
)
⋅
R
(
z
)
E'(z)=G_D(z)\cdot E(z)=G_D(z)\cdot\Phi_{e}(z) \cdot R(z)
E′(z)=GD(z)⋅E(z)=GD(z)⋅Φe(z)⋅R(z)
通常情况下,并不需要对输入进行Z变换,用不上
【简单在s域开环传函判断一下系统型别就好】
补充:无纹波最小拍系统设计
如其描述,最小拍设计进入稳态后,在非采样时刻一般仍存在纹波。
本节的要求是在非采样时刻,不存在纹波
无纹波判断方法
- 假设系统最高阶为 t q t^{q} tq阶,那么开环传函至少应该包括 q q q个积分环节【 1 s q \frac{1}{s^q} sq1】
这是废话,不然系统跟踪不上
- 应该保证调节后误差传函
E
′
(
z
)
E'(z)
E′(z)为
z
−
1
z^{-1}
z−1的有限多项式,其中
E ′ ( z ) = D ( z ) E ( z ) = D ( z ) Φ e ( z ) R ( z ) E'(z)=D(z)E(z)=D(z)\Phi_e(z)R(z) E′(z)=D(z)E(z)=D(z)Φe(z)R(z)
由着一条,可以推出下面的结论:设计的闭环传函要包括开环传函的全部零点
无纹波设计思路
只有一条,闭环传函
Φ
(
z
)
\Phi(z)
Φ(z)除了要满足最少拍要求形式外,还需要包含开环传函
G
(
z
)
G(z)
G(z)的全部零点
【因此,无纹波最小拍系统比有纹波最小拍多出的拍数,就是开环传函单位圆内的零点数】
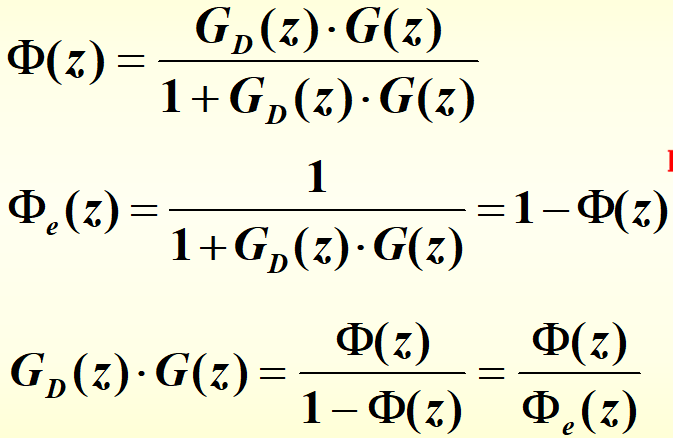
![[support2022@cock.li].faust、[tsai.shen@mailfence.com].faust勒索病毒数据怎么处理|数据解密恢复](https://img-blog.csdnimg.cn/533484f21558448a87465a7dc1e85625.png)