【算法训练-动态规划二】【线性DP问题】最长递增子序列

news2024/10/6 22:19:08

废话不多说，喊一句号子鼓励自己：程序员永不失业，程序员走向架构！本篇Blog的主题是【动态规划】，使用【数组】这个基本的数据结构来实现，这个高频题的站点是：CodeTop，筛选条件为：目标公司+最近一年+出现频率排序，由高到低的去牛客TOP101去找，只有两个地方都出现过才做这道题（CodeTop本身汇聚了LeetCode的来源），确保刷的题都是高频要面试考的题。
在这里插入图片描述
明确目标题后，附上题目链接，后期可以依据解题思路反复快速练习，题目按照题干的基本数据结构分类，且每个分类的第一篇必定是对基础数据结构的介绍。

最长递增子序列【MID】

终于又来到一道看了很久的高频题目这里

题干

注意「子序列」和「子串」这两个名词的区别，子串一定是连续的，而子序列不一定是连续的
在这里插入图片描述

解题思路

按照动态规划的思路进行状态设计和状态转移方程编写，这里用数学归纳法进行状态转移公式的推导。

数学归纳法：比如我们想证明一个数学结论，那么我们先假设这个结论在 k < n 时成立，然后根据这个假设，想办法推导证明出 k = n 的时候此结论也成立。如果能够证明出来，那么就说明这个结论对于 k 等于任何数都成立

我们设计动态规划算法，不是需要一个 dp 数组吗？我们可以假设 dp[0...i-1] 都已经被算出来了，然后问自己：怎么通过这些结果算出 dp[i]

1 定义状态（定义子问题）

我们的定义是这样的：dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度，这个定义中 nums[i] 必须被选取，且必须是这个子序列的最后一个元素；

2 状态转移方程（描述子问题之间的联系）

算法演进过程中每个 dp[i] 的结果是我们肉眼看出来的，我们应该怎么设计算法逻辑来正确计算每个 dp[i] 呢？这就是动态规划的重头戏，如何设计算法逻辑进行状态转移，才能正确运行呢？这里需要使用数学归纳的思想：

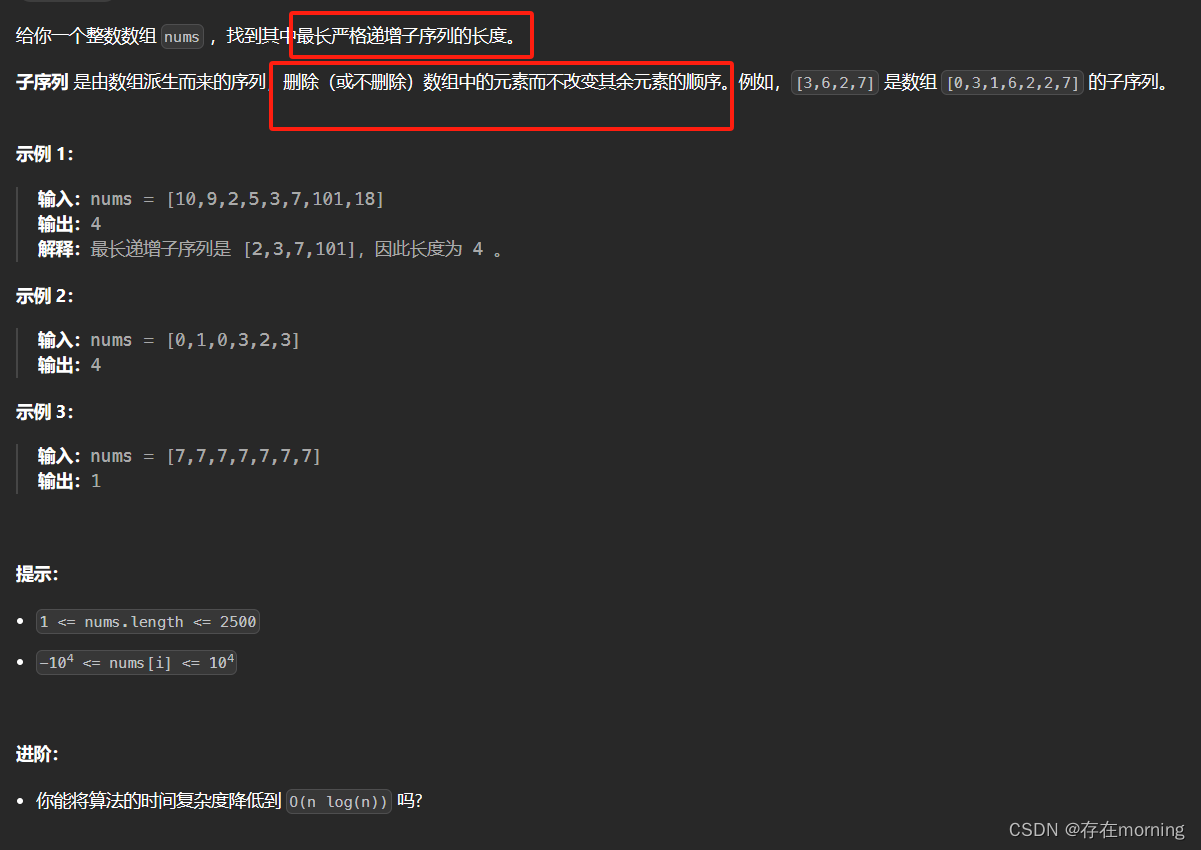
假设我们已经知道了 dp[0…4] 的所有结果，我们如何通过这些已知结果推出 dp[5] 呢

在这里插入图片描述
根据刚才我们对 dp 数组的定义，现在想求 dp[5] 的值，也就是想求以 nums[5] 为结尾的最长递增子序列。

nums[5] = 3，既然是递增子序列，我们只要找到前面那些结尾比 3 小的子序列，然后把 3 接到这些子序列末尾，就可以形成一个新的递增子序列，而且这个新的子序列长度加一

nums[5] 前面有哪些元素小于 nums[5]？这个好算，用 for 循环比较一波就能把这些元素找出来。
以这些元素为结尾的最长递增子序列的长度是多少？回顾一下我们对 dp 数组的定义，它记录的正是以每个元素为末尾的最长递增子序列的长度

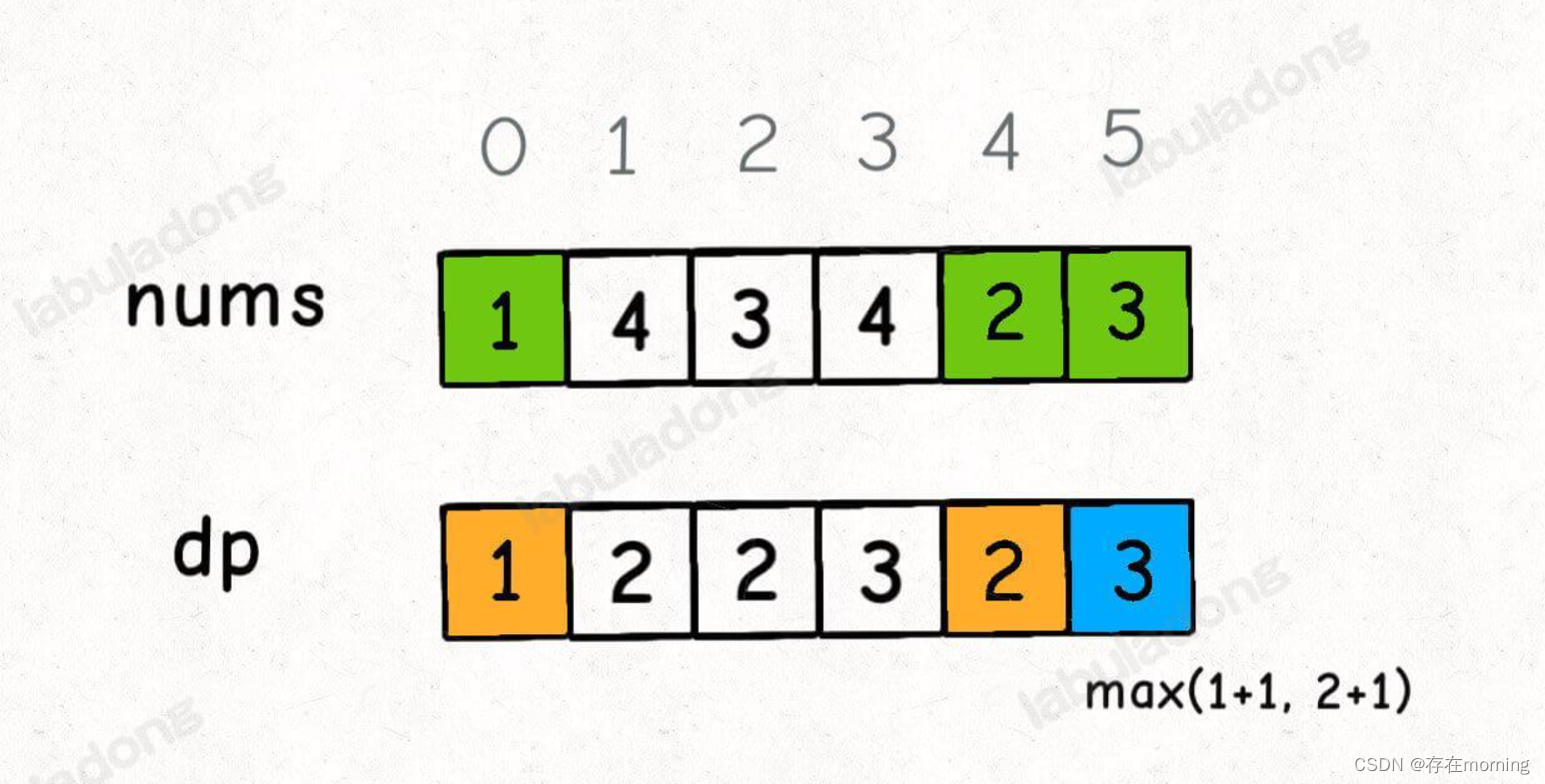
在这里插入图片描述
以我们举的例子来说，nums[0] 和 nums[4] 都是小于 nums[5] 的，然后对比 dp[0] 和 dp[4] 的值，我们让 nums[5] 和更长的递增子序列结合，得出 dp[5] = 3

for (int j = 0; j < i; j++) {
    if (nums[i] > nums[j]) {
        dp[i] = Math.max(dp[i], dp[j] + 1);
    }
}

3 初始化状态

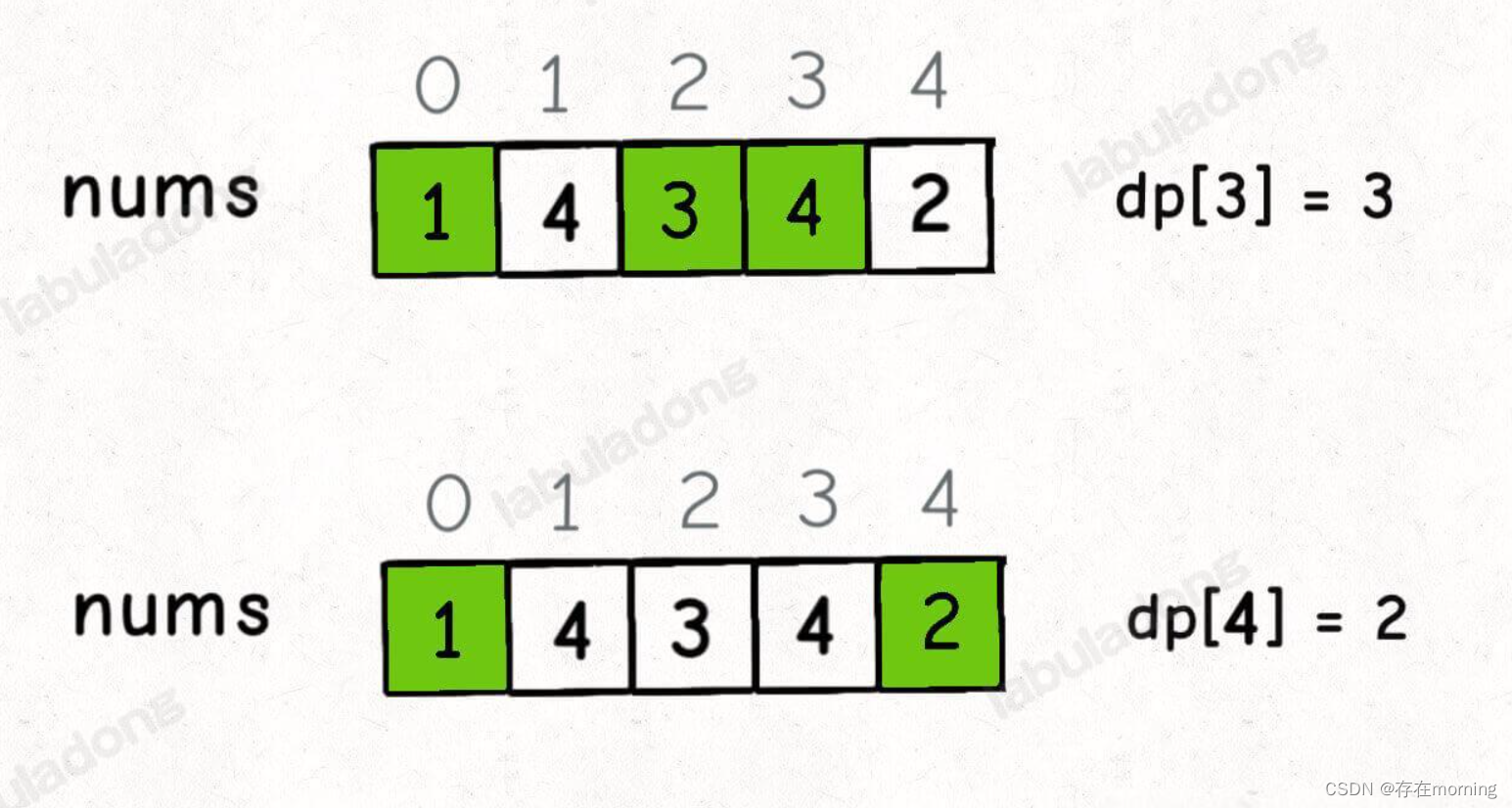
根据这个定义，我们就可以推出 base case：dp[i] 初始值为 1，因为以 nums[i] 结尾的最长递增子序列起码要包含它自己
在这里插入图片描述

4 求解方向

这里采用自底向上，从最小的状态开始求解

5 找到最终解

根据这个定义，我们的最终结果（子序列的最大长度）应该是 dp 数组中的最大值

int res = 0;
for (int i = 0; i < dp.length; i++) {
    res = Math.max(res, dp[i]);
}
return res;

代码实现

给出代码实现基本档案

基本数据结构：数组
辅助数据结构：无
算法：动态规划
技巧：无

其中数据结构、算法和技巧分别来自：

10 个数据结构：数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树
10 个算法：递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法
技巧：双指针、滑动窗口、中心扩散

当然包括但不限于以上

import java.util.*;

class Solution {
    // 最长上升子序列
    public int lengthOfLIS(int[] nums) {
        // 1 入参校验判断
        if (nums.length < 1) {
            return -1;
        }

        // 2 定义DP数组：dp[i]表示以nums[i]为结尾的上升子序列的最大长度
        int[] dp = new int[nums.length];

        // 3 base case, 所有元素都至少包含自己，且dp[0]=1 因为只有一个元素,二者合并
        Arrays.fill(dp, 1);

        // 4 状态转移，填充状态转移表
        for (int i = 1; i < nums.length; i++) {
            // dp[i]为i之前的小于nums[i]的所有dp[i]的最大值组成
            for (int j = 0; j < i; j++) {
                if (nums[j] < nums[i]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
        }

        // 5 最终解为dp数组的最大值
        int result = 0;
        for (int i = 0; i < dp.length; i++) {
            result = Math.max(result, dp[i]);
        }

        return result;
    }
}

当然最值的更新也可以在双重循环中同步进行

import java.util.*;

class Solution {
    // 最长上升子序列
    public int lengthOfLIS(int[] nums) {
        // 1 入参校验判断
        if (nums.length < 1) {
            return -1;
        }

        // 2 定义DP数组：dp[i]表示以nums[i]为结尾的上升子序列的最大长度
        int[] dp = new int[nums.length];

        // 3 base case, 所有元素都至少包含自己，且dp[0]=1 因为只有一个元素,二者合并
        Arrays.fill(dp, 1);

        // 4 状态转移，填充状态转移表
        int result = 1;
        for (int i = 1; i < nums.length; i++) {
            // dp[i]为i之前的小于nums[i]的所有dp[i]的最大值组成
            for (int j = 0; j < i; j++) {
                if (nums[j] < nums[i]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
            result = Math.max(result, dp[i]);
        }

        return result;
    }
}