【算法训练-动态规划四】【子序列类型问题】连续子数组的最大和

news2025/2/26 3:31:52

废话不多说，喊一句号子鼓励自己：程序员永不失业，程序员走向架构！本篇Blog的主题是【动态规划】，使用【数组】这个基本的数据结构来实现，这个高频题的站点是：CodeTop，筛选条件为：目标公司+最近一年+出现频率排序，由高到低的去牛客TOP101去找，只有两个地方都出现过才做这道题（CodeTop本身汇聚了LeetCode的来源），确保刷的题都是高频要面试考的题。
在这里插入图片描述

名曲目标题后，附上题目链接，后期可以依据解题思路反复快速练习，题目按照题干的基本数据结构分类，且每个分类的第一篇必定是对基础数据结构的介绍。

连续子数组的最大和【MID】

来从动态规划最简单的题开始训练

题干

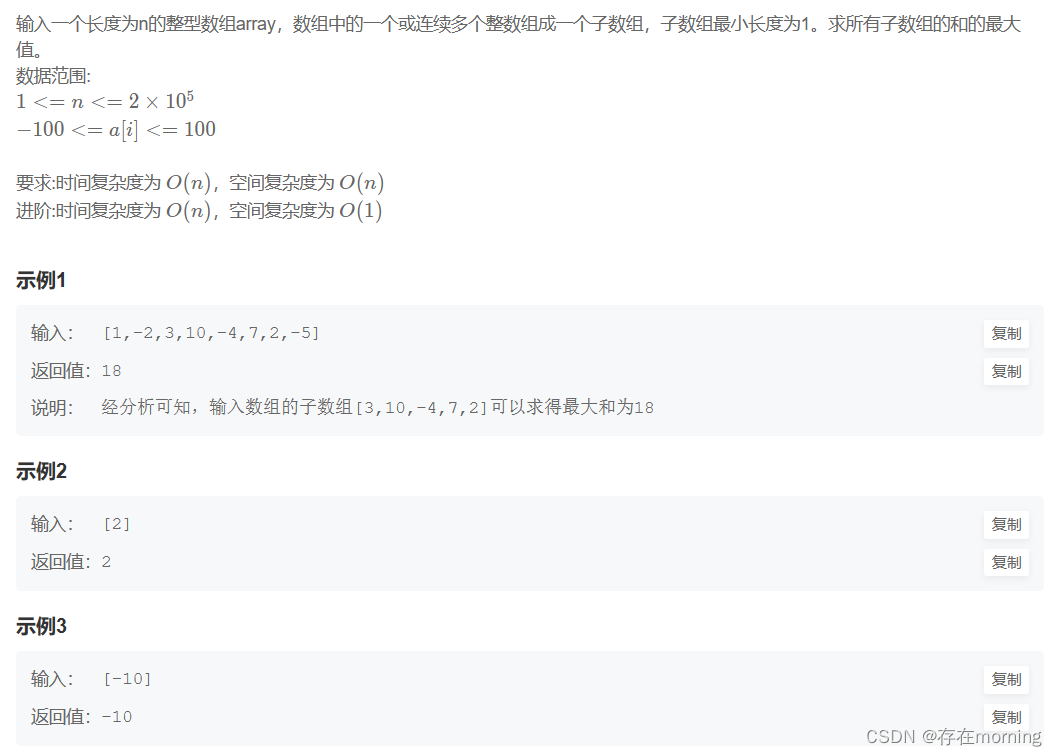
直接粘题干和用例
题干中可以提炼的关键信息：连续的子数组，整数有正有负，求连续子数组的最大和，题目要我们找出和最大的连续子数组的值是多少，「连续」是关键字，连续很重要，不是子序列。题目只要求返回结果，不要求得到最大的连续子数组是哪一个。这样的问题通常可以使用「动态规划」解决

解题思路

按照动态规划的思路进行状态设计和状态转移方程编写

1 定义状态（定义子问题）

dp[i]：表示以 nums[i] 结尾的连续子数组的最大和。说明：「结尾」和「连续」是关键字。

2 状态转移方程（描述子问题之间的联系）

根据状态的定义，由于 nums[i] 一定会被选取，并且以 nums[i] 结尾的连续子数组与以 nums[i - 1] 结尾的连续子数组只相差一个元素 nums[i] 。假设数组 nums 的值全都严格大于 0，那么一定有 dp[i] = dp[i - 1] + nums[i]。可是 dp[i - 1] 有可能是负数，于是分类讨论：

如果 dp[i - 1] > 0，那么可以把 nums[i] 直接接在 dp[i - 1] 表示的那个数组的后面，得到和更大的连续子数组；
如果 dp[i - 1] <= 0，那么 nums[i] 加上前面的数 dp[i - 1] 以后值不会变大。于是 dp[i] 「另起炉灶」，此时单独的一个 nums[i] 的值，就是 dp[i]。

以上两种情况的最大值就是 dp[i] 的值，写出如下状态转移方程：
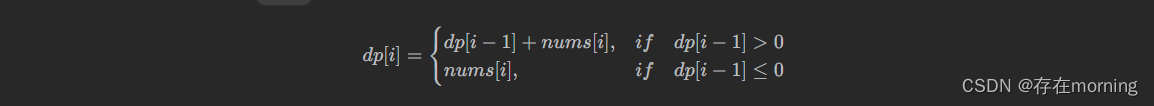
在这里插入图片描述

3 初始化状态

dp[0] 根据定义，只有 1 个数，一定以 nums[0] 结尾，因此 dp[0] = nums[0]

4 求解方向

这里采用自底向上，从最小的状态开始求解

5 找到最终解

这里的dp[i]只是以i为结尾的连续子数组的最大和，并不是题目中的问题，数组的连续子数组最大和，所以最终解并不是子问题的解，需要用一个MAX值承载，通过与dp[i]比较更新最终解

代码实现

给出代码实现基本档案

基本数据结构：数组
辅助数据结构：无
算法：动态规划
技巧：无

其中数据结构、算法和技巧分别来自：

10 个数据结构：数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树
10 个算法：递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法
技巧：双指针、滑动窗口、中心扩散

当然包括但不限于以上

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param array int整型一维数组
     * @return int整型
     */
    public int FindGreatestSumOfSubArray (int[] array) {
        // 1 定义dp数组，初始化状态,初始化最终解
        int[] dp = new int[array.length];
        dp[0] = array[0];
        int greatSum = dp[0];

        // 2 定义状态转移方程
        for (int i = 1; i < array.length; i++) {
            // 状态转移方程，求解当前的dp[i]
            dp[i] = dp[i - 1] <= 0 ? array[i] : dp[i - 1] + array[i];
            // 更新最大值
            greatSum = Math.max(greatSum, dp[i]);
        }

        return greatSum;
    }
}

复杂度分析

时间复杂度：遍历了一遍数组，所以时间复杂度为O（N）
空间复杂度：定义了动规数组，空间复杂度为O（N）

拓展知识：回顾动态规划

动态规划（Dynamic Programming，简称DP）是一种解决复杂问题的算法设计技术，常用于优化问题和组合问题的求解。它通过将原问题分解成子问题，并保存子问题的解，以避免重复计算，从而提高算法的效率。动态规划通常用于解决具有重叠子问题和最优子结构性质的问题。

动态规划的基本思想可以总结为以下几个步骤：

定义问题的状态：首先要明确定义问题的状态，这些状态可以用来描述问题的各种情况。
找到状态转移方程：状态转移方程描述了问题之间的联系，即如何从一个状态转移到另一个状态。这通常涉及到问题的递归关系，通过这个关系可以从较小规模的子问题得到更大规模的问题的解。
初始化状态：确定初始状态的值，这通常是问题规模最小的情况下的解。
自底向上或自顶向下求解：动态规划可以采用自底向上（Bottom-Up）或自顶向下（Top-Down）的方式求解问题。自底向上是从最小的状态开始逐步计算，直到得到最终问题的解；自顶向下是从最终问题开始，递归地计算子问题的解，直到达到最小状态。
根据问题的要求，从状态中找到最终解。