文章目录
- 一、递归遍历二叉树
- 1.1 前序遍历
- 1.2 中序遍历
- 1.3 后序遍历
- 二、非递归遍历二叉树
- 2.1 前序遍历
- 2.2 中序遍历
- 2.3 后序遍历
- 三、高效的 Morris 遍历
- 3.1 前序遍历
- 3.2 中序遍历
- 3.3 后序遍历
关于二叉树的遍历也是面试过程中非常有可能考的话题。
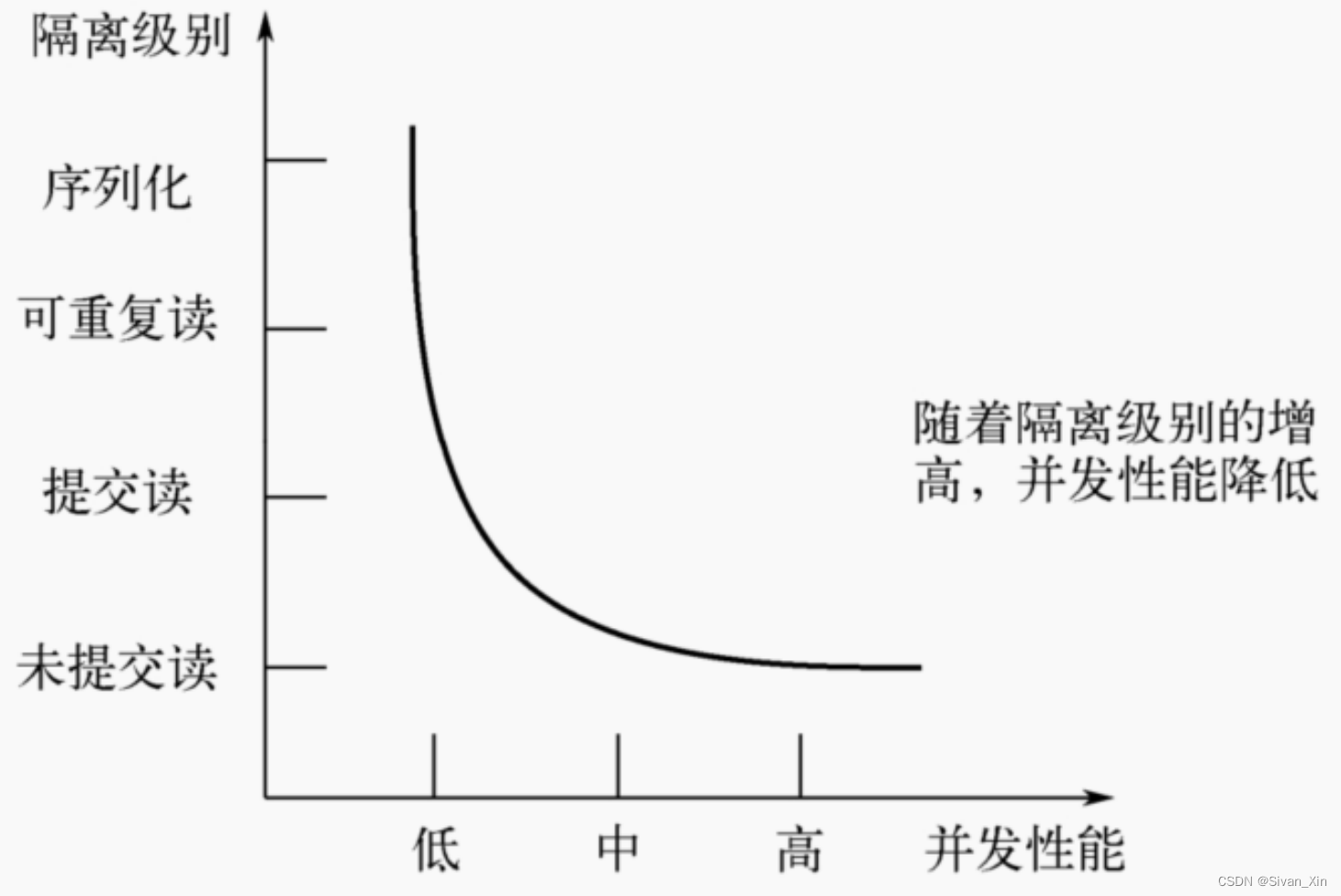
常见的简单的递归遍历二叉树,非常的基础,显而易见,这并不会是面试官想要的看的遍历二叉树的方法。一般来说,非递归实现二叉树的遍历才是考得相对较多的,时间复杂度 O(N),空间复杂度 O(N)
如果我们能够在空间复杂度为 O(1)的条件下实现二叉树的遍历,这将是一个很好的加分项,这就是文章后面介绍的 Morris 遍历

那么接下来我们先回顾一下递归和非递归的方法遍历二叉树的做法,然后介绍 Morris 遍历
二叉树节点(TreeNode)
class TreeNode {
int val = 0; //值
TreeNode left = null; //左节点
TreeNode right = null; //右节点
public TreeNode(int val) {
this.val = val;
}
}
一、递归遍历二叉树
按照如图所示进行二叉树的遍历,遍历的节点顺序如图所示。

我们会发现每个节点都会遍历到三次,先序遍历的结果就是节点被第一次遇见的顺序,中序遍历的结果就是节点被第二次遇见的顺序,后序遍历的结果就是节点被第三次遇见的顺序
1.1 前序遍历
前序遍历二叉树的顺序是,根——》左——》右
basecase:
当节点 root 为null 时,即遇见了空节点,就可以直接返回了
递归过程:
获取到一棵二叉树后,但凡遇见的节点不是空节点,那么我们就将其放到结果列表中,然后分别遍历该节点的左子树和右子树。那么对于子树处理方式也是一样的
public class Solution1 {
public List<Integer> list = new ArrayList<>(); //返回的结果列表
public List<Integer> preorderTraversal (TreeNode root) {
if(root == null) {
return list;
}
func1(root);
return list;
}
public void func1(TreeNode root) {
if(root == null) {
return; //basecase
}
list.add(root.val);//添加到结果列表中
func1(root.left); //遍历左子树
func1(root.right);//遍历右子树
}
}
1.2 中序遍历
中序遍历二叉树的顺序是,左——》根——》右
本质上和前序遍历的没有什么不同,不过是写在了同一个方法中
public class Solution2 {
List<Integer> list = new ArrayList<>();
public List<Integer> inorderTraversal(TreeNode root) {
if(root == null)
return list;
inorderTraversal(root.left); //遍历左子树
list.add(root.val); //添加到结果列表中
inorderTraversal(root.right); //遍历右子树
return list;
}
}
1.3 后序遍历
中序遍历二叉树的顺序是,左——》右——》根
public class Solution3 {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
if(root == null) return list;
List<Integer> leftTree = postorderTraversal(root.left);
list.addAll(leftTree);//将左子树的后序遍历结果放到结果列表中
List<Integer> rightTree = postorderTraversal(root.right);
list.addAll(rightTree);//将右子树的后序遍历结果放到结果列表中
list.add(root.val);
//此时左子树和右子树后序遍历的结果放好了,就将当前根节点值放到结果列表中
return list;
}
}
二、非递归遍历二叉树
非递归遍历实际上将就是将压栈这个步骤自己进行实现
2.1 前序遍历
前序遍历是 根、左、右 这样的顺序,那么就应该先把根节点入栈

然后弹出一个节点,即当前的根节点,保存到结果列表 list 中。并且只要当前的根节点的左右节点不为空,就将他们压入栈。先压右节点,再压左节点。因为栈是先进后出的,为了先处理左子树,就应该让左节点在右节点后入栈

只要栈不为空,我们就继续弹出一个节点,进行保存,当前弹出的是栈顶的 B 节点,说明开始处理左子树了

等到下一轮 D 节点都弹出时,说明以 B 节点为根节点的子树已经处理完毕了,接下来要开始处理以 C 节点为根节点的子树,依次类推,直到栈为空,循环结束
public class Solution1 {
public ArrayList<Integer> list = new ArrayList<>();//结果列表
public void func2(TreeNode root) {
Stack<TreeNode> stack = new Stack<>();
stack.push(root);//先将根节点入栈
//只要栈不为空就一直循环
while (!stack.isEmpty()) {
TreeNode cur = stack.pop();//弹出元素,当前的根
list.add(cur.val);//保存
//先压右节点,再压左节点
if (cur.right != null) {
stack.push(cur.right);
}
if (cur.left != null) {
stack.push(cur.left);
}
}
}
}
2.2 中序遍历
中序遍历的顺序是 左、根、右
只要 root 节点不为空,就不断的将其左子节点压入栈中,root 在走到 root 的左节点上

遇见空节点,那么该空节点必然是其父节点的左节点(左子树处理完毕),此时从栈中弹出一个节点便是该子树的根节点,进行保存。然后让 root 走到方才弹出的根节点的右子树上,继续处理右子树的内容,处理的方式同上

显而易见,此时 root 为空,那么只要 root 不为空或者栈不为空循环都会继续,继续从栈中弹出节点,进行保存。
直到弹出节点 A,进行保存,此时栈为空了。但是 root 不为空,指向节点 A 的右子树上的根节点 C 呢,循环继续。也就是说,此时节点 A 的左子树处理完毕,根处理完毕,开始处理右子树。
以此类推,直到栈中没有节点了,root 也为空了,一切就真的结束了
public class Solution2 {
public ArrayList<Integer> list = new ArrayList<>();//结果列表
public void func2(TreeNode root) {
Stack<TreeNode> stack = new Stack<>();
while (root != null || !stack.isEmpty()) {
//一股脑将左边界都添加到栈中,直到遇见null
while (root != null) {
stack.push(root);
root = root.left;
}
//此时的root为null了,弹出一个元素,走到其右子树中
TreeNode node = stack.pop();
list.add(node.val);
root = node.right;//对于右子树的处理方法同上
}
}
}
2.3 后序遍历
后序遍历的思想和前序遍历的思想非常的像。
已知后序遍历的顺序是 左、右、根。栈的特点就是先进后出,那么如果我们遍历二叉树以根、右、左 的顺序使用一个收集栈保存节点,是可以做到的(模仿前序遍历,区别就是先压左节点再压右节点)。
最后再将收集栈中的节点一个个弹出,就是左、右、根的顺序
public class Solution3 {
public ArrayList<Integer> list = new ArrayList<>();//结果列表
public void func2(TreeNode root) {
Stack<TreeNode> stack1 = new Stack<>();//压栈
Stack<Integer> stack2 = new Stack<>();//收集栈
stack1.push(root);//先压入根节点
while (!stack1.isEmpty()) {
TreeNode node = stack1.pop();//弹出一个元素,将其值放到收集栈中
stack2.push(node.val);
//方才弹出的元素,有左先压左,有右再压右
if (node.left != null) {
stack1.push(node.left);
}
if (node.right != null) {
stack1.push(node.right);
}
//周而复始
}
//将收集栈中的元素倒出来
//stack1的出栈顺序是根右左,压入到stack2中再弹出来,就是左右根
while (!stack2.isEmpty()) {
list.add(stack2.pop());
}
}
}
三、高效的 Morris 遍历
在上面的遍历方式中时间复杂度为 O(N),因为要遍历每个节点。空间复杂度为 O(N),因为使用到了栈,无论是递归使用的系统的栈还是非递归自己手动创建的栈。
Morris 遍历是一种和上面的遍历方式不太一样的遍历方式,通过利用树中的空节点,来达到节省空间的目的,空间复杂度为 O(1)
遍历介绍:
有一个 TreeNode 类型的变量 cur 此时正在根节点处
- 如果 cur 节点没有左孩子,cur 直接移动到右孩子上
- 如果 cur 节点有左孩子,那就找到左子树上最右的节点 Rightmost
- 若 Rightmost 节点的右指针指向空,那就让右指针指向 cur,然后 cur 向左边移动
- 若 Rightmost 节点的右指针已经指向 cur 了,那就让它指向 null,然后cur 往右移
- cur 为空,遍历结束
遍历过程:
此时的 cur 指向 A 节点,有左孩子,且左子树上的最右节点是 B 节点,那就让 B 的右指针指向 cur,cur 往左子树上移动

发现 cur 依旧有左孩子,按照之前的做法进行操作。cur 即将移动到其左孩子 D 节点上

终于发现 cur 没有左孩子了,那就往其右子树移动

此时的 cur 没有左孩子,cur 就往 G 节点的右子树上移动,回到了 B 节点

cur 回到 B 节点后,B 节点有左子树,并且左子树的最右节点 Rightmost 正指向 cur 呢,那就让它给指回 null,恢复原样,然后 cur 往其右孩子上移动

cur 往 B 节点的右孩子移动,就又回到了 A 节点,A 节点有左子树,并且左子树的最右节点正指向 cur(A 节点),就将其恢复原样,重新指向 null,然后 cur 往其右孩子上移动

这样子一来,这个二叉树的左子树以及根节点算是遍历完成了,接下来的右子树也是同样的规则进行遍历

直到 cur 为空,遍历就算结束了

我们可以发现,所有的拥有左子树的节点都遍历了两次,其余的节点只遍历了一次
代码实现:
public class Solution5 {
public static void Morris (TreeNode root) {
if (root == null) {
return;
}
TreeNode cur = root;
TreeNode rightMost = null;
while (cur != null) {
rightMost = cur.left;//开始找左子树中最右的节点
if (rightMost == null) {
//没有左孩子
cur = cur.right;
}else {
//有左孩子
//先让 rightMost 指向 cur 左子树的最右节点
while (rightMost.right != null && rightMost.right != cur) {
rightMost = rightMost.right;
}
//到这里,rightMost 的 right 可能为 null,可能为 cur
if (rightMost.right == cur) {
//说明是第二遍到 cur 节点
rightMost.right = null;//让其回归正常
cur = cur.right;
}else {
//第一遍来到 cur 节点
rightMost.right = cur;
cur = cur.left;
}
}
}
}
}
3.1 前序遍历
对于前序遍历来说,如果某个节点没有左孩子,只会遍历到一次,就直接打印。如果有左孩子的,说明可以遍历到两次,那么第一次遍历到的时候打印

红色部分就是前序遍历的节点顺序,和预期的一模一样
public class Solution5 {
public static void preMorris (TreeNode root) {
if (root == null) {
return;
}
TreeNode cur = root;
TreeNode rightMost = null;
while (cur != null) {
rightMost = cur.left;
if (rightMost == null) {
System.out.println(cur.val);//唯一一次遍历,打印
cur = cur.right;
}else {
while (rightMost.right != null && rightMost.right !=cur) {
rightMost = rightMost.right;
}
if (rightMost.right == cur) {
//说明是第二遍到 cur 节点
rightMost.right = null;
cur = cur.right;
}else {
//第一遍来到 cur 节点
System.out.println(cur.val);//第一次出现,打印
rightMost.right = cur;
cur = cur.left;
}
}
}
}
}
3.2 中序遍历
对于中序遍历来说,如果某个节点没有左孩子,只会遍历到一次,就直接打印。如果有左孩子的,说明可以遍历到两次,那么第二次遍历到的时候打印

public class Solution5 {
public static void inMorris (TreeNode root) {
if (root == null) {
return;
}
TreeNode cur = root;
TreeNode rightMost = null;
while (cur != null) {
rightMost = cur.left;
if (rightMost == null) {
System.out.println(cur.val);//唯一一次遍历,打印
cur = cur.right;
}else {
while (rightMost.right != null && rightMost.right !=cur) {
rightMost = rightMost.right;
}
if (rightMost.right == cur) {
//说明是第二遍到 cur 节点
System.out.println(cur.val);//第二次出现,打印
rightMost.right = null;
cur = cur.right;
}else {
//第一遍来到 cur 节点
rightMost.right = cur;
cur = cur.left;
}
}
}
}
}
3.3 后序遍历
对于后序遍历来说,如果某个节点没有左孩子,那就不管了。
如果有左孩子并且是第二次到达该节点,那么就将该节点的左子树的右边界逆序打印。
一切完成之后,将整棵树的右边界进行逆序打印


如图所示,在 Morris 遍历中, A 和 B 是拥有左子树的节点且是第一次遍历,跳过。D 和 G 都没有左子树,跳过。
又遍历到了 B 节点,这是第二次遍历到 B 节点,并且 B 节点还是第二次遍历到,所以就逆序打印 B 节点左子树的右边界 G D,后面的节点就依次根据这些内容来判断。
直到遍历完全之后,逆序打印整棵树的右边界
注:在第二遍遍历到该节点的时候,需要先进行还原二叉树,即将对应的 Rightmost 的 right 指向 null,然后在进行逆序打印右边界操作
public static void postMorris (TreeNode root) {
if (root == null) {
return;
}
TreeNode cur = root;
TreeNode rightMost = null;
while (cur != null) {
rightMost = cur.left;//开始找左子树中最右的节点
if (rightMost == null) {
//没有左孩子
cur = cur.right;
}else {
//有左孩子
while (rightMost.right != null && rightMost.right !=cur) {
rightMost = rightMost.right;
}
if (rightMost.right == cur) {
//说明是第二遍到 cur 节点
rightMost.right = null;//先让其回归正常
printFunc(cur.left);//逆序打印
cur = cur.right;
}else {
//第一遍来到 cur 节点
rightMost.right = cur;
cur = cur.left;
}
}
}
printFunc(root);//最后总的逆序打印整棵树的右边界
}
//提供了一个树的根节点,逆序打印这棵树的右边界
public static void printFunc(TreeNode root) {
TreeNode tail = reverseRightEdge(root);
TreeNode cur = tail;//进行一个反转
while (cur != null) {
System.out.println(cur.val);
cur = cur.right;
}
reverseRightEdge(tail);//给它反转回去
}
//反转右边界(类似于反转单链表)
public static TreeNode reverseRightEdge(TreeNode root) {
TreeNode cur = root;
TreeNode prev = null;
while (cur != null) {
TreeNode curNext = cur.right;
cur.right = prev;
prev = cur;
cur = curNext;
}
return prev;
}