网络流探索：解决网络最大流问题的算法集锦

1.初识网络流

网络流一直是初学者心中很难过去的一道坎，很多人说它是一个不像DFS/BFS那么直观的算法，同时网上也有各种参差不齐的材料，让人感到一知半解。
如果你也有这样的感觉，那么不要灰心，坚持住，因为网络流是组合优化理论的明珠，是你走向计算机理论深邃奥秘的第一步。
路径这个概念虽然非常基础，但是有着很多的应用，例如，可以把交通网络看成一个图，那么图上的路径就是一个合法的交通路线，我们可以通过最短路径算法求出最佳的路径。同样我们可以把社会网络，也就是人和人的关系看成一个网络，我们可以用路径来分析社会网络的各种性质关系；甚至我们可以把编写的程序看成一个图，可以通过路径建模程序当中的性质，例如，可以证明程序当中犯的某一些错误是否会发生，这些都是在图论的基础上建立的各种各样有趣的应用。

2.最大流问题的定义与基础

最大流问题属于图论的范畴，这里的图是有向有权图，边都有方向和权重，图中有很多节点，其中一个节点是起点，记作s，还有一个节点是终点，记作t。
可以这样理解最大流问题：我们希望把水从节点s送到终点t，水要通过管道来输送，这些管道就是图中的边，边都有权重，权重可以理解为管道的容量，否则可能会导致压力过大导致管道爆裂，那么，给定管道的限制，那么最大流是多少？
第一步创建residual graph，它的权重等于水管的空闲量，初始时没有水流，所以空闲量等于容量；
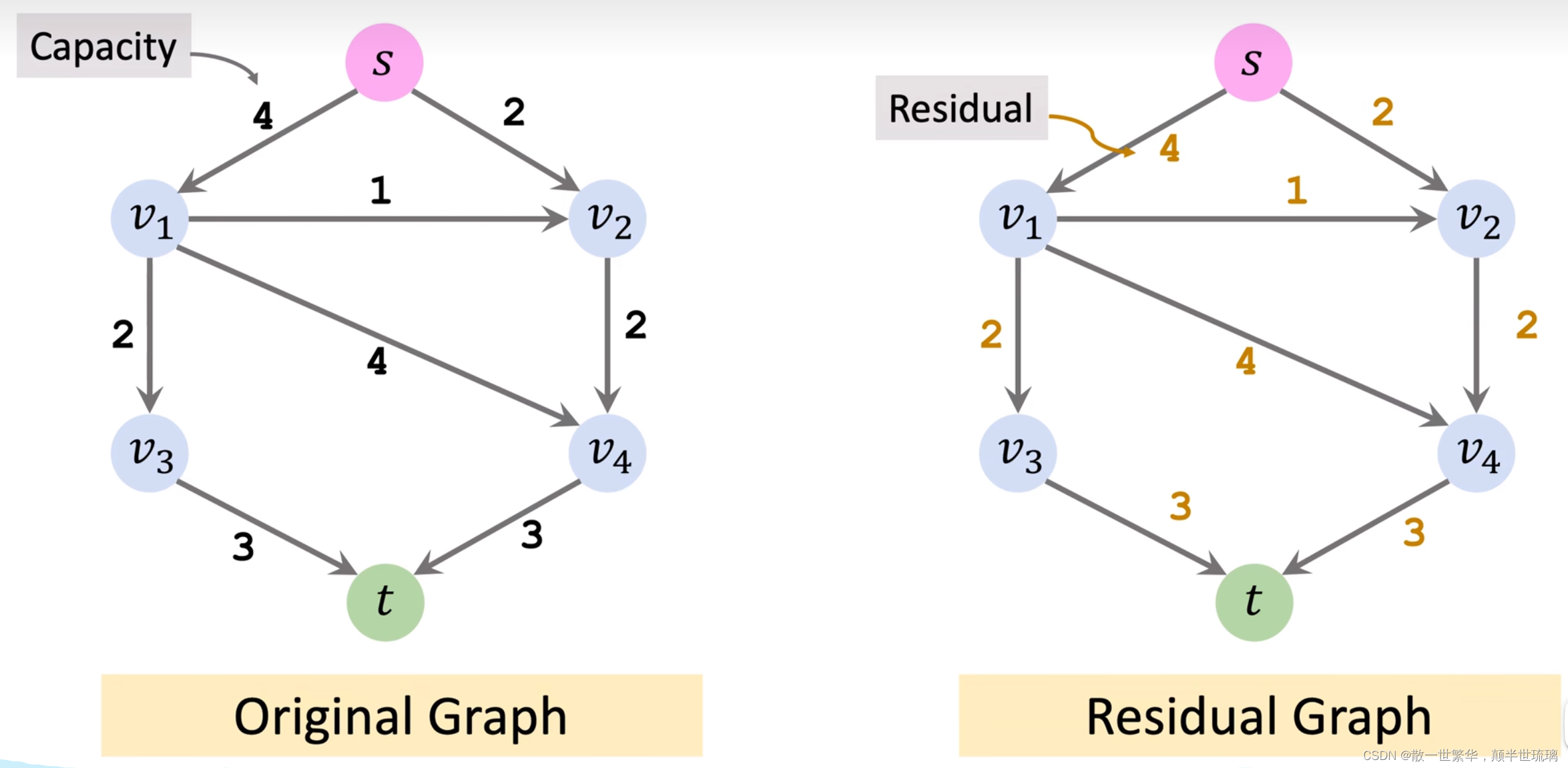
在这里插入图片描述
最直观的简单算法为：
第二步是在residual graph找到augumenting path，augumenting path是指从起点s到终点t的简单路径，寻找路径上最小的权重，假设最小权重为x，那么该路径下最多只能传输x单位的水流，再多的话，最弱的水管会爆裂。此外，我们让x单位的水流过这条路径，那么这条路径下所有边的空闲量都要减去x，不断重复第二步的过程，直到找不到起点到终点的路径，这就说明没有办法把更多的水从起点送到终点，这时候就应该终止循环！
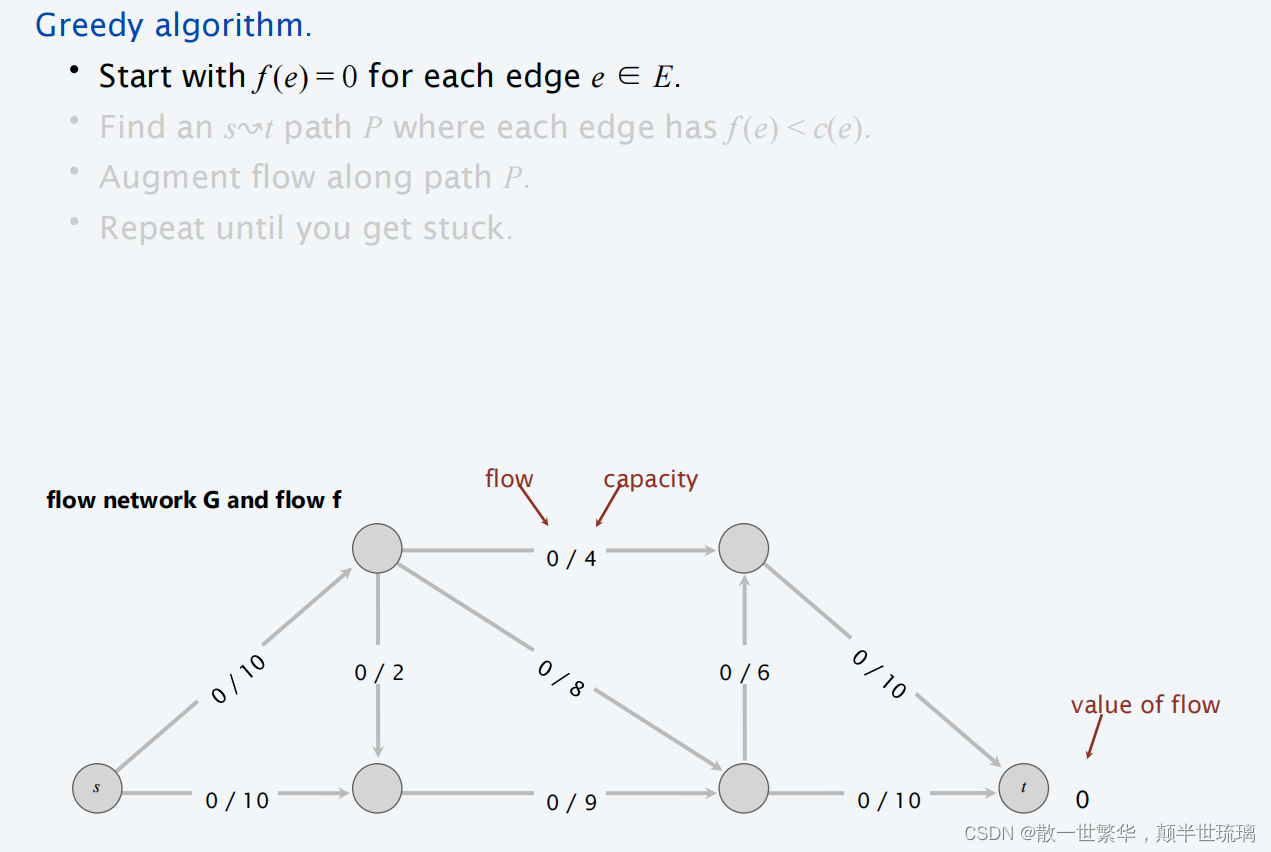
在这里插入图片描述
**简单算法有时候会失败！**这种算法只能找到blocking flow阻塞流，阻塞流意思是把网络给阻塞了，没办法传输更多的水流，阻塞流未必是最大流。具体示例如下所示：

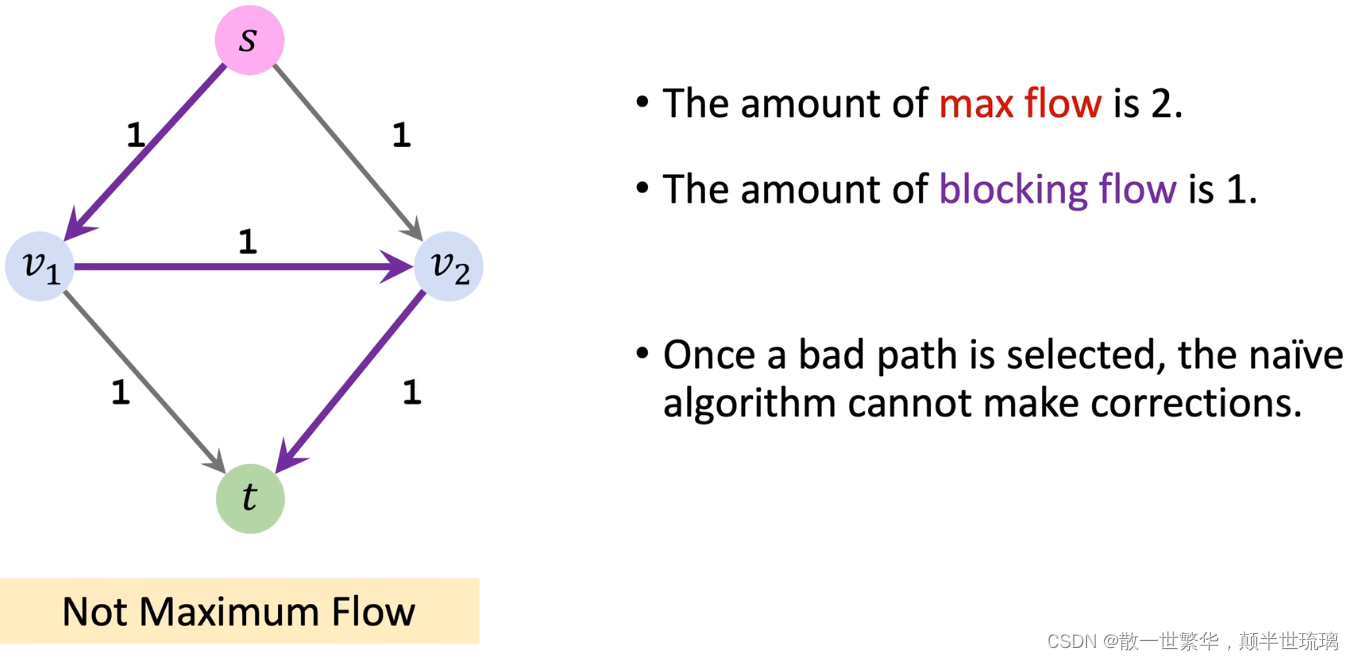
这说明简单算法不能保证结果是最大流，后序介绍的算法可以保证求出的结果一定是最大流。

3.Ford–Fulkerson algorithm

前面说简单算法不一定找到最大流，究其原因主要是简单算法不会反悔，不能纠正错误，一旦坏的路径被选中，算法就无法找到最大流。
但是Ford–Fulkerson algorithm一定可以找到最大流，因为它可以把不好的路径给撤销掉。
Ford–Fulkerson algorithm与简单算法相比，唯一的区别是添加一条反向的路径，这样一来，就算之前选择的路径不好，也可以原路撤销返回。
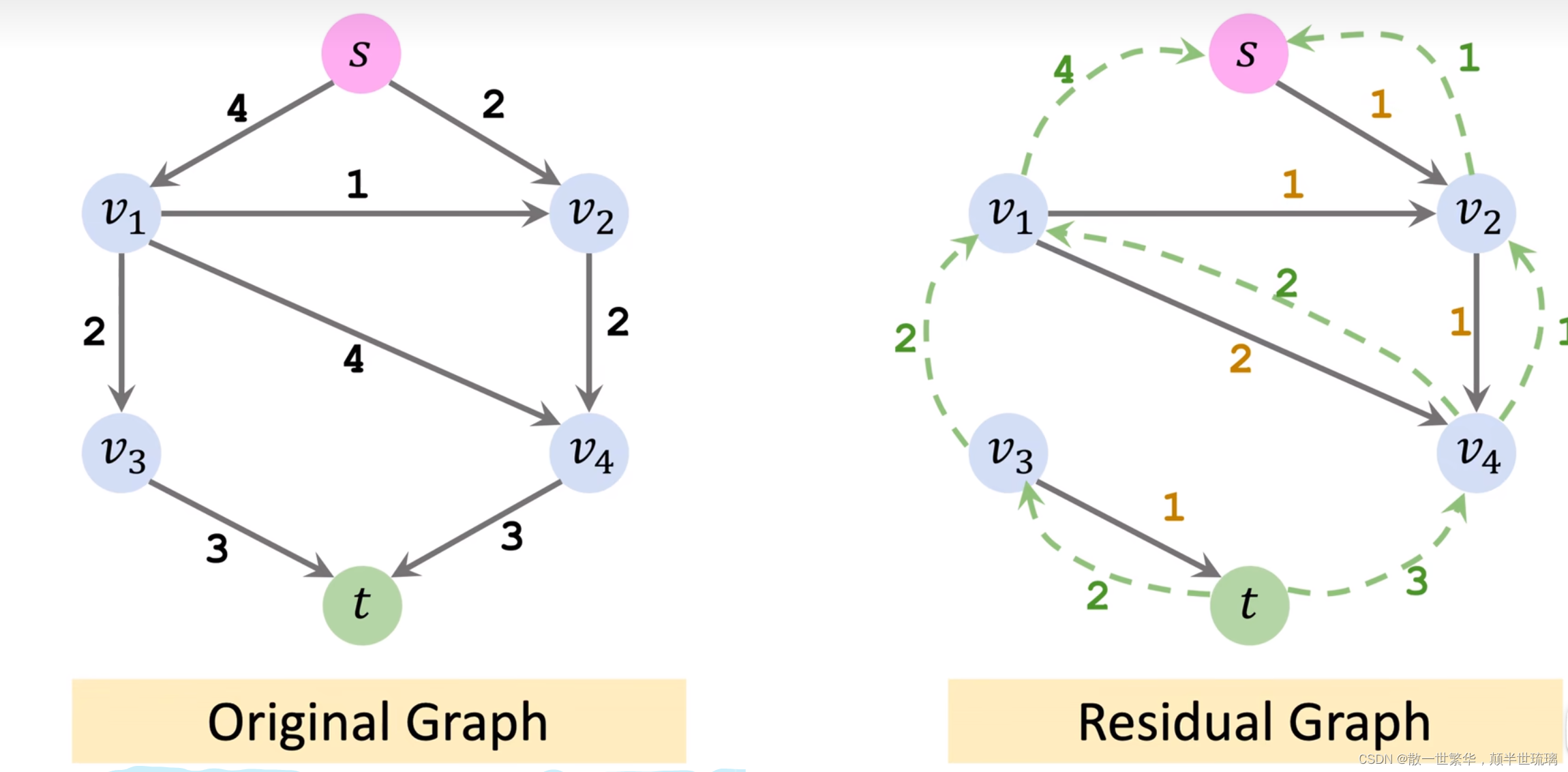
在这里插入图片描述
Ford-Fulkerson算法是一种用于解决网络最大流问题的经典算法。它基于寻找增广路径的思想，通过不断寻找增广路径来增加流量，直到无法找到增广路径为止。
该算法的步骤如下：

创建一个residual graph并初始化所有边的流量为0。
当存在从源节点到汇节点的增广路径时：
- 使用深度优先搜索或广度优先搜索来寻找一条增广路径。增广路径是指路径上的每条边的剩余容量大于0。
- 在找到增广路径后，通过更新路径上的边的剩余容量来增加流量。
- 更新路径上的边的剩余容量，即减少正向边的剩余容量，增加反向边的剩余容量。
当无法找到增广路径时，算法终止。此时，得到的流就是最大流。

需要注意的是，Ford-Fulkerson算法的时间复杂度很慢，并且会在某些情况下陷入无限循环，因此为了保证算法的终止和收敛性，通常需要采用其他技术，如Edmonds-Karp算法中使用的最短增广路径策略。
总之，Ford-Fulkerson算法是一种通过不断寻找增广路径来逐步增加流量的经典算法，用于解决网络最大流问题。

4.Edmonds-Karp Algorithm

Edmonds-Karp论文发表在1972年，比Ford–Fulkerson algorithm晚了12年，Edmonds-Karp算法不是新的算法，而是Ford–Fulkerson algorithm算法的特例，Edmonds和Karp的贡献在于他们证明了更好的时间复杂度，时间复杂度不依赖于最大流的大小。Edmonds-Karp Algorithm与Edmonds-Karp Algorithm几乎完全一样，唯一的区别在于Edmonds-Karp Algorithm寻找路径的时候要用最短路径算法。

Edmonds-Karp算法是Ford-Fulkerson算法的一种改进版本，用于求解网络最大流问题。它通过使用广度优先搜索来选择最短增广路径，从而提高算法的效率和收敛速度。
以下是Edmonds-Karp算法的详细步骤：

初始化所有边的流量为0。
While 存在从源节点到汇节点的增广路径：
- 使用广度优先搜索来找到一条最短增广路径。最短增广路径是指路径上的边数最少，即最短距离最短。
- 在找到最短增广路径后，计算路径上的最小剩余容量。最小剩余容量是指路径上所有边的剩余容量的最小值。
- 通过更新路径上的边的流量来增加流量，即在正向边上增加流量，或在反向边上减少流量。
- 更新路径上的边的剩余容量，即减少正向边的剩余容量，增加反向边的剩余容量。
当不存在从源节点到汇节点的增广路径时，算法终止。此时，得到的流就是最大流。
Edmonds-Karp算法通过使用广度优先搜索来选择最短增广路径，相比于Ford-Fulkerson算法的深度优先搜索，它能够更快地找到增广路径。这是因为广度优先搜索以层次化的方式逐层遍历网络，从而找到最短距离的路径。这种选择最短增广路径的策略确保了算法的收敛性和终止性。
总结来说，Edmonds-Karp算法是一种基于广度优先搜索的改进Ford-Fulkerson算法，用于求解网络最大流问题。它通过选择最短增广路径来提高算法的效率和收敛速度。

从图中可以看出，这个时间复杂度比Ford-Fulkerson算法要好的多，因为它不依赖于网络流的大小。Edmonds和Karp两个人更好的贡献是证明了更好的时间复杂度，下面会简单分析一下Edmonds-Karp算法的时间复杂度。
主要意思就是：假设residual graph有m条边，n个点，算法的每一轮循环都要在residual graph中寻找无权的最短路，所以需要O(m)的时间复杂度，原因是，如果原图中有m条边，那么residual graph中最多有m条反向边，所以residual graph一共有不超过2m条边，如果一个无权图有2m条边，那么寻找最短路就需要O(m)的时间。此外，Edmonds和Karp两个人证明了算法最多循环mn轮，即，算法每一轮需要O(m)的时间，最多循环mn轮，所以最坏时间复杂度是 $O(m^2n)$ ,这个时间复杂度与最大流无关，最大流可以是几百几千万，都不会影响时间复杂度的大小。

5.Dinic’s Algorithm

Dinic’s Algorithm它是寻找网络最大流的算法，它的时间复杂度比Edmonds-Karp Algorithm更低，先简单比较一下两种算法的时间复杂度，具体如下所示：
在这里插入图片描述
从图中可以看出，若边的数量为m，点的数量为n，则Edmonds-Karp Algorithm的时间复杂度为O( $m^2n$ ),而Dinic’s Algorithm的时间复杂度为O( $mn^2$ ),但是一般边的个数m会远大于点的个数n，因此Dinic’s Algorithm的时间复杂度会更低。
Dinic’s Algorithm要用到Blocking Flow（阻塞流），阻塞流意思是拥有这些流量，就不能增加更多流量，也就是这些流量阻塞了管道。
最大流一定是阻塞流，但是阻塞流未必是最大流。 前面介绍的简单算法一定能找到阻塞流，但是未必能找到最大流。
此外，Dinic’s Algorithm还会用到Level Graph ，下面简单介绍一下Level Graph。
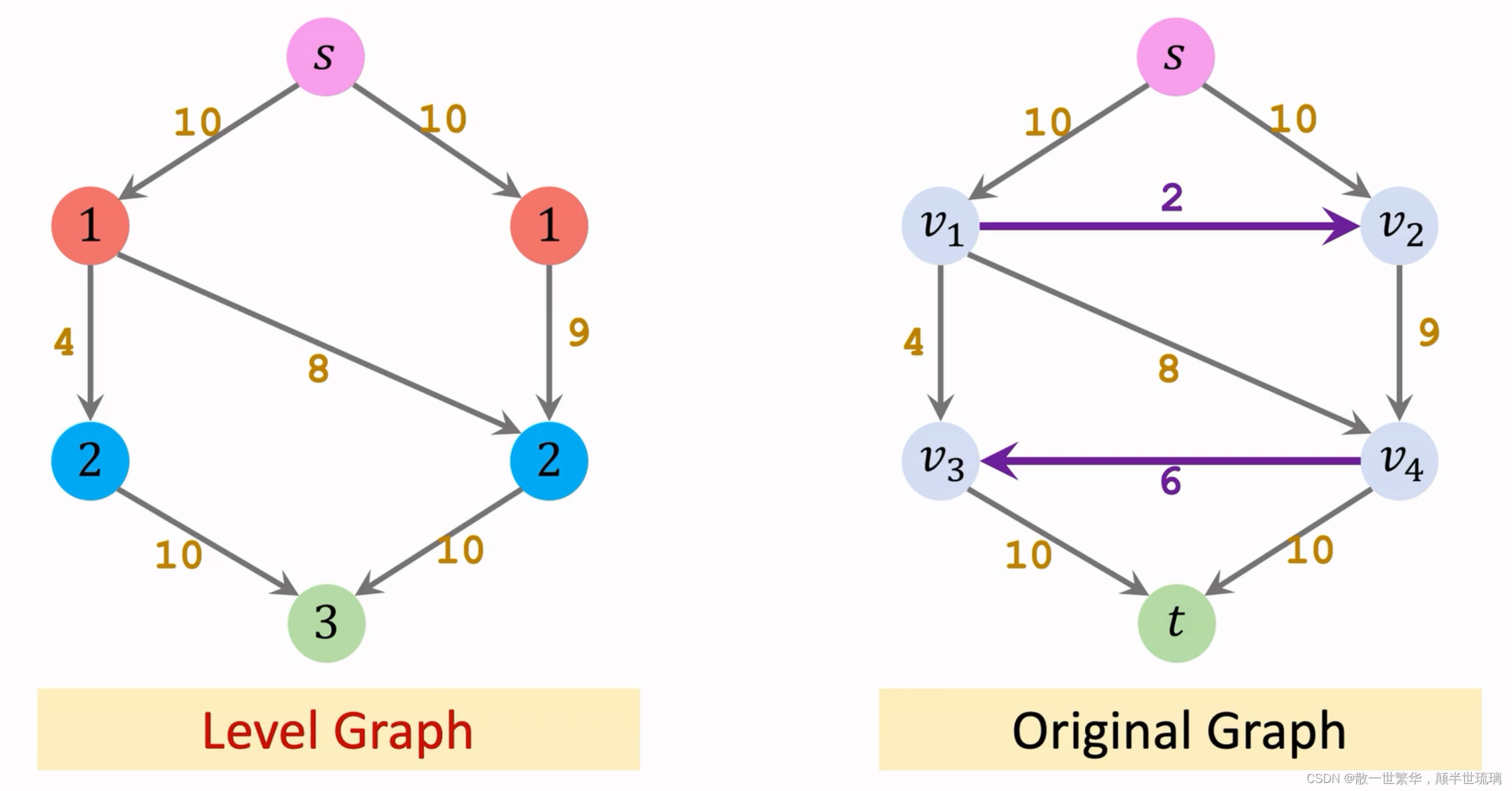
给定右边的原图，下面一步步构造Level Graph，从起点S开始，走一步能达到 $v_{1},v_{2}$ 这两个节点，把 $v_{1},v_{2}$ 加入左边的Level Graph，同时把 $v_{1},v_{2}$ 记作第一层，意思是从起点出发走一步能达到，保留从起点S到第一层的边。再看右边的原图，从第一层的 $v_{1},v_{2}$ 出发，走一步能达到 $v_{3},v_{4}$ 两个节点，把 $v_{3},v_{4}$ 加入左边的Level Graph，同时把 $v_{3},v_{4}$ 记作第二层，意思是从起点出发走两步能达到，保留从第一层到第二层的三条边。再看右边的原图，从第二层的节点 $v_{3},v_{4}$ 出发。走一步可以达到终点t，把终点t加入左边的Level Graph，同时把终点t记作第三层，意思是从起点出发走三步能达到，并保留第二层到第三层的边，Level Graph的边指的是从上一层到下一层。，下图右侧两条紫色的边分别是从第一层到第一层，第二层到第二层，因此不能加入Level Graph中。
在这里插入图片描述
掌握了与预备知识，那么下面进入正题！
Dinic’s算法是一种高效的解决最大流问题的算法，它基于增广路径和分层图的概念。以下是Dinic’s算法的步骤总结：

构建初始残余网络（residual graph）：将所有边的流量初始化为0，并根据网络中的边构建初始的残余网络（residual graph）。
构建分层图（Level Graph）：使用广度优先搜索（BFS）构建分层图。分层图是在残余网络中，将每个节点按照其到源节点的最短距离分层的图。
寻找增广路径：在分层图中，从源节点到汇节点寻找增广路径。增广路径是指路径上所有边的剩余容量大于0。
更新阻塞流和反向边：如果找到增广路径，则将对应residual graph路径上的最小剩余容量作为阻塞流，增加流量，并更新路径上的边的剩余容量。同时，对于路径上的每条边，增加反向边的剩余容量。
重复迭代：重复步骤2到步骤4，直到无法再找到增广路径为止。每次迭代中，分层图（Level Graph）会更新，从而更好地指导下一次增广路径的寻找。
终止条件：当无法再找到增广路径时，算法终止。此时，得到的流就是最大流。
Dinic’s算法通过构建分层图(Level Graph)来指导增广路径的寻找，从而减少了无效的搜索，提高了算法的效率。在寻找增广路径时，除了更新阻塞流和路径上的边的剩余容量外，还需要增加反向边的剩余容量，以确保反向流的正确性。
![在这里插入图片描述](https://img-blog.csdnimg.cn/e82e433f7a91418d891a1c6d62c1f6fe.png

6.Minimum Cut Problem

Minimum Cut Problem翻译为最小割问题，最小割与最大流是等价的。
可以这样理解最小割问题，Cut的意思是割断一些管道，让水不能从起点s流向终点t，Min-Cut最小割的目标是让割断的水管总容量最小，也就是说，我尽量割断细的管道，而不是粗的管道，我用最小的力气就能截断水流。
对于同一张图，有不同的切断方式，左边的割量为3，是最小割，而右边的割为6，它不是最小割！此外，还需要注意，最小割的并不唯一！
在这里插入图片描述

7.Max-Flow Min-Cut Theorem

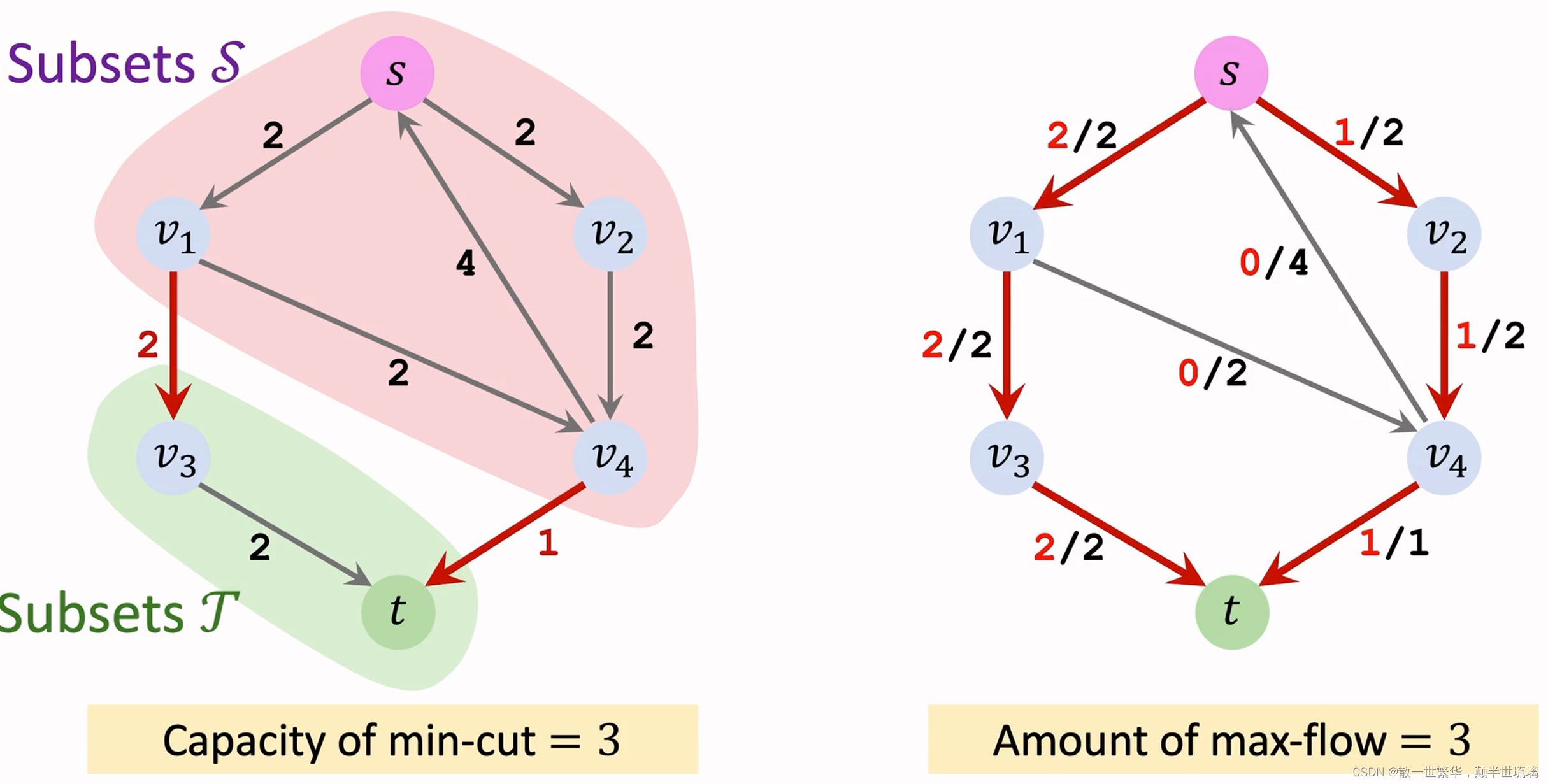
最大流最小割定理（Max-Flow Min-Cut Theorem）说明了最大流问题和最小割问题的等价性！
对于一个网络流问题，最大流的流量等于最小割的容量，也就是说，你求出了最大流问题，就相当于求出了最小割问题。这个定理是Ford和Fulkerson两个人在1962年提出来的。
在这里插入图片描述
接下来介绍一种寻找最小割问题！
这种方法把最小割问题等价转换为最大流问题，只要我们找到最大流，我们就能找到最小割。
简单来说就是：
1.使用Edmonds-Karp Algorithm找到最终的residual graph；
2.然后在最终的residual graph去掉所有的反向边；
3.在去掉所有反向边的residual graph后，从该图中找到从s出发能到达的所有顶点，让其作为集合的一部分，剩下的作为集合的剩余部分；
4.最后根据划分好的两部分集合找到最小割。
在这里插入图片描述