首先来看期望的基本公式

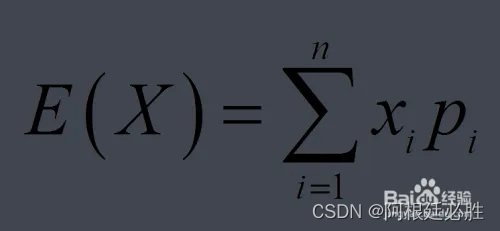
其中x是抛x次，p是在抛第x次后出现连续正面的概率

先来看出现1次正面的期望

按照公式来算是

抛1次 1/2的概率

抛2次 1/4的概率

抛3次 1/8的概率...

我们可以写一个程序试一下

signed main()
{
	ios_base::sync_with_stdio(0); cin.tie(0),cout.tie(0);
	double z=0.5,f=0.5;
	double res=0;
	for(int i=1;i<100000;i++)
	{
		res+=i*z;
		z*=f;
	}
	cout<<res<<'\n';
}

每次都需要多乘一个反面的概率，跑个1e5次最后的结果是2

其实我们也可以不用这公式

设抛x次需要的期望是E(x)

E(1)=E(0)+0.5*1+0.5*(1+E(1))

就是刚开始是E(0)也就是抛0次连续的正面需要的期望是0

E(0) 接下来有两个操作

0.5的概率正面就是结束了也就是0.5*1,1是操作次数

0.5的概率反面，也就是继续抛直到抛到E(1)的时候结束0.5(1+E(1)),1+E(1)是操作次数

所以E(1)=E(0)+0.5*1+0.5*(1+E(1))

由上面可以推出E(x)=E(x-1)+0.5*1+0.5*(1+E(x))

应该可以通过矩阵快速幂求递推式

矩阵快速幂后面再补上