递归子程序

使用不带回溯的递归子程序解析文法是预测性语法分析的基础，这通常需要该文法是LL(1)文法。每个非终结符对应一个递归子程序，并使用当前的输入符号和FIRST集合来决定调用哪个产生式。

让我们以一个简单的文法为例：

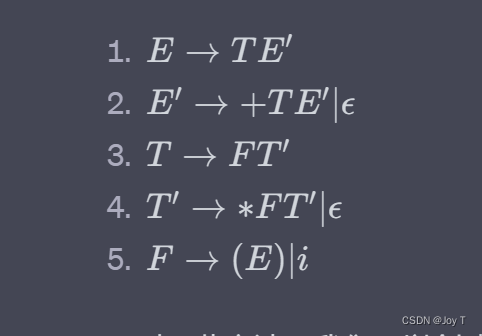
对于此文法，我们可以创建以下不带回溯的递归子程序（以Python为例理解意思）：

def E():
    T()
    E_prime()

def E_prime():
    if lookahead == '+':
        match('+')
        T()
        E_prime()

def T():
    F()
    T_prime()

def T_prime():
    if lookahead == '*':
        match('*')
        F()
        T_prime()

def F():
    if lookahead == '(':
        match('(')
        E()
        match(')')
    elif lookahead == 'i':
        match('i')
    else:
        raise Exception("Syntax Error")
#并不是只有 F 能报错，在实际的编译器或解释器的实现中，任何递归子程序都可能会遇到预期之外的输入，并报告语法错误。
        
def match(expected_token):
    global lookahead
    if lookahead == expected_token:
        lookahead = get_next_token()  # Update the lookahead with the next input symbol.
    else:
        raise Exception("Syntax Error")

在这里，lookahead变量存储当前的输入符号，get_next_token()方法会获取输入中的下一个符号。递归子程序使用FIRST集合预测下一步，如果lookahead匹配某个产生式的开始，那么该产生式被执行。每一个非终结符都会被写成一个函数，这个函数对应着该非终结符所有可能推导到的集合！递归子程序的目的是处理非终结符对应的所有推导可能性，而不仅仅是FIRST集。

在递归子程序中，FIRST集主要用于指导语法分析器决定接下来应该如何进行。但一旦决策被作出（例如，在E_prime()中当lookahead == '+'时），该子程序就会根据相应的产生式继续进行，并可能递归地调用自己或其他子程序，以处理非终结符的所有可能的推导。

为了完整地解析输入，我们需要确保我们的递归子程序能够处理对应非终结符的所有推导可能性，这包括其FIRST集，但不限于此。在有些情况下，这还需要考虑递归推导，以处理重复的结构或模式。

同时，当编写这些递归子程序时，我们应当确保输入的文法是LL(1)的，这意味着每个非终结符的FIRST集合中的每个产生式对应的集合是不相交的，并且对于任何可能产生\epsilon的产生式，FIRST和FOLLOW集合也是不相交的。

---

完整的预测性语法分析器

上面给出的只是子程序。为了形成一个完整的预测性语法分析器，我们需要一个main函数或者一个驱动程序来初始化整个过程并开始解析。下面是如何将这些子程序组成一个简单的预测性语法分析器的例子：

# 假设我们有一个从输入源获取下一个符号的函数
def get_next_token():
    # 这里是一个简单的模拟实现
    global input_string, position
    if position < len(input_string):
        token = input_string[position]
        position += 1
        return token
    else:
        return None  # 表示输入结束

# 全局变量
input_string = "i+i*i"  # 你的输入字符串，这里是一个例子
position = 0
lookahead = get_next_token()  # 初始化lookahead

# 前面定义的递归子程序...

def main():
    E()  # 从文法的开始符号开始
    if lookahead is not None:
        print("Syntax Error: Unexpected symbol", lookahead)
    else:
        print("Parsing successful!")

if __name__ == "__main__":
    main()

这里的main函数简单地开始解析过程，并检查是否成功地到达了输入的末尾。如果在解析结束时lookahead不是None，则输入中还有未处理的符号，这表示一个语法错误。如果解析成功地完成，则输出相应的消息。

---

举例

例如，考虑输入为+i+i+i：

• 第一次调用E_prime()会匹配第一个+，然后调用T()匹配i，最后再次递归调用E_prime()。
• 在这次递归调用中，会匹配第二个+，再次调用T()匹配第二个i，然后再次递归调用E_prime()。
• 在最后一次调用中，会匹配第三个+，调用T()匹配第三个i，然后再次递归调用E_prime()，此时由于没有更多的+，所以这次调用不会执行任何操作并立即返回。

递归调用E_prime()的目的是允许多个连续的+TE'结构。这实际上使我们能够解析如+T+T+T这样的输入，每一个+T都对应于E' —> +TE'的一个实例。如果我们移除递归调用E_prime()，那么子程序只能匹配一个+T结构，无法正确解析像+i+i+i这样的输入。