This way
题意:
一开始以为是水题,敲了一个二分+贪心检查的代码,20分。发现从根往某个节点x走的时候,一路走来的子树上的节点到已栽树的节点的距离会变短,那么并不能按照初始情况贪心。
于是就想着检查时候用线段树,存的是(每个节点最晚开始时间-它距离最近栽树的点的距离)往后就将这个称为ddl。每一步都往当前最小值的位置走,每走一步,将当前这一步的子树区间+1,如此往复。当走到一个点发现已经走的步数>这个点最晚开始时间时候就是not。但是代码过于繁杂,最终放弃了这样思路,而且常数可能会比较大,最终如果TLE了血亏。
首先这道题的答案满足二分的性质,考虑使用二分。二分出来结束时间的时候,我们可以求出每个点的最晚到达时间,首先分c>=0和c<0两种情况。对于c<0的时候又要分三种情况。其实就是等差数列求和公式,但是注意会爆longlong,所以转乘为除。我这里使用二分去找答案,当然直接算好像也行?
发现其实每个点的ddl就是它子树的ddl最小值,也就是每个点的ddl可视为子树中最小ddl-当前点到ddl最小的节点的距离,例如:
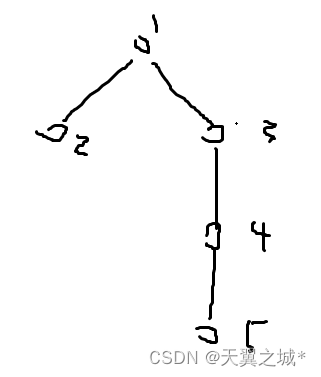
假设点1的最晚开始时间是第10天,点2是第3天,点3是第50天,点4是第90天,点5是第4天。那么转换过来,其实它们真实的ddl如下:
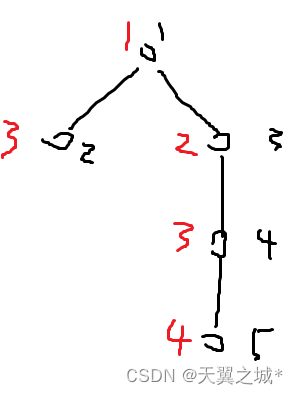
这个时候我们只需要将所有真·ddl存到桶里面,再做一个前缀和,记为num[i]。若i<num[i],则表示你走了i步,但是有超过i个点的ddl在i步之内(我们在上图处理完之后,所有链上的ddl必然是递增的也就是如果点x需要走10步,那father[x]最大为9,father[father[x]]最大为8,也就是为x做铺垫),那么表示无法在i步内满足num[i]个点的ddl。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e5+5;
ll a[N],b[N],c[N],en[N],e,shou,mo;
int n,x,y,dep[N],u,tim,num[N],t[N];
vector<int>vec[N];
bool vis[N];
#define pii pair<int,int>
vector<pii>day;
int dfs(int x,int fa){
for(int ne:vec[x]){
if(ne==fa)continue;
t[x]=min(t[x],dfs(ne,x)-1);
}
num[t[x]]++;
return t[x];
}
bool check(ll d){
day.clear();
memset(num,0,sizeof num);
for(int i=1;i<=n;i++){
ll l=1,r=min(1ll*n,d);t[i]=-1;
while(l<=r){
ll x=l+r>>1;
if(c[i]>=0){
if((a[i]*2ll+d-x)/(d-x+1)<=2*b[i]+(x+d)*c[i])t[i]=x,l=x+1;
else r=x-1;
}
else{
c[i]=-c[i];
if(en[i]<=x){
if(a[i]<=d-x+1)t[i]=x,l=x+1;
else r=x-1;
}
else if(en[i]<=d){
e=en[i]-1;
shou=b[i]-x*c[i],mo=b[i]-e*c[i];
if((2*a[i]-2*(d-e)+e-x)/(e-x+1)<=(shou+mo))t[i]=x,l=x+1;
else r=x-1;
}
else{
ll shou=b[i]-x*c[i],mo=b[i]-d*c[i];
if((2*a[i]+d-x)/(d-x+1)<=(shou+mo))t[i]=x,l=x+1;
else r=x-1;
}
c[i]=-c[i];
}
}
if(t[i]-dep[i]<=0)return 0;
}
dfs(1,0);
for(int i=1;i<=n;i++){
num[i]+=num[i-1];
if(num[i]>i)
return 0;
}
return 1;
}
int main()
{
ll l=n,r=0,ans=-1;
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%lld%lld%lld",&a[i],&b[i],&c[i]);
r=max(r,a[i]);
if(c[i]<0)
en[i]=(b[i]-c[i]-1)/(-c[i]);
}
r=min(r,1000000000ll);
for(int i=1;i<n;i++){
scanf("%d%d",&x,&y);
vec[x].push_back(y),vec[y].push_back(x);
}
while(l<=r){
ll mid=l+r>>1;
if(check(mid))r=mid-1,ans=mid;
else l=mid+1;
}
printf("%lld\n",ans);
return 0;
}


![[SQL开发笔记]SELECT DISTINCT语句:返回唯一不同的值](https://img-blog.csdnimg.cn/74ed1928d0e84498bba3e200d1e905f4.png)

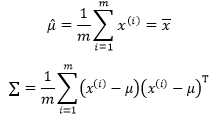



![[SQL开发笔记]SELECT 语句:读取数据表的信息](https://img-blog.csdnimg.cn/ad4002024ccb464cb599450024c23078.png)